The Nature of Order

The four books of The Nature of Order constitute the ninth, tenth, eleventh and twelfth in a series of books which describe an entirely new attitude to architecture and building. The books are intended to provide a complete working alternative to our present ideas about architecture, building, and planning — an alternative which will, we hope, gradually replace current ideas and practices.

| Volume 1 | THE TIMELESS WAY OF BUILDING | | Volume 2 | A PATTERN LANGUAGE | | Volume 3 | THE OREGON EXPERIMENT | | Volume 4 | THE LINZ CAFE | | Volume 5 | THE PRODUCTION OF HOUSES | | Volume 6 | A NEW THEORY OF URBAN DESIGN | | Volume 7 | A FORESHADOWING OF 21ST CENTURY ART: THE COLOR AND GEOMETRY OF VERY EARLY TURKISH CARPETS | | Volume 8 | THE MARY ROSE MUSEUM | | Volumes 9 to 12 | THE NATURE OF ORDER: AN ESSAY ON THE ART OF BUILDING AND THE NATURE OF THE UNIVERSE | | Book 1 | THE PHENOMENON OF LIFE | | Book 2 | THE PROCESS OF CREATING LIFE | | Book 3 | A VISION OF A LIVING WORLD | | Book 4 | THE LUMINOUS GROUND |

Future volume now in preparation

| Volume 13 | BATTLE: THE STORY OF A HISTORIC CLASH BETWEEN WORLD SYSTEM A AND WORLD SYSTEM B |

THE NATURE OF ORDER

An Essay on the Art of Building and the Nature of the Universe

BOOK ONE THE PHENOMENON OF LIFE

BOOK TWO THE PROCESS OF CREATING LIFE

BOOK THREE A VISION OF A LIVING WORLD

BOOK FOUR THE LUMINOUS GROUND

THE CENTER FOR ENVIRONMENTAL STRUCTURE in BERKELEY CALIFORNIA in association with PATTERNLANGUAGE.COM

© 2002 CHRISTOPHER ALEXANDER

PREVIOUS VERSIONS

© 1980, 1983, 1987, 1993, 1995, 1996, 1998, 1999, 2000, 2001 CHRISTOPHER ALEXANDER

Published by The Center for Environmental Structure 2701 Shasta Road, Berkeley, California 94708

CES is a trademark of the Center for Environmental Structure. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of the Center for Environmental Structure.

ISBN 978-0-9726529-1-9 (Book 1) ISBN 978-0-9726529-0-2 (Set)

LIBRARY OF CONGRESS CATALOGING-IN-PUBLICATION DATA

Alexander, Christopher. The Nature of Order: An Essay on the Art of Building and the Nature of the Universe / Christopher Alexander, p. cm. (Center for Environmental Structure Series; v. 9-12).

Contents: v.1. The Phenomenon of Life — v.2. The Process of Creating Life v.3. A Vision of a Living World — v.4. The Luminous Ground

1. Architecture—Philosophy. 2. Science—Philosophy. 3. Cosmology
2. Geometry in Architecture. 5. Architecture—Case studies. 6. Community
3. Process philosophy. 8. Color (Philosophy).

I. Center for Environmental Structure. II. Title. III. Title: The Phenomenon of Life. IV. Series: Center for Environmental Structure series; v. 9.

NA2500.A444 2002 720.1—dc21 2002154265 ISBN 978-0-9726529-1-9 (cloth: alk. paper: v.1)

Typography by Katalin Bende and Richard Wilson Manufactured in China by Everbest Printing Co., Ltd.

BOOK ONE: THE PHENOMENON OF LIFE

PROLOGUE TO BOOKS 1-4

THE ART OF BUILDING AND THE NATURE OF THE UNIVERSE . . . . . 1

PREFACE . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

PART ONE

1. THE PHENOMENON OF LIFE . . . . . . . . . . . . . . . . 27
2. DEGREES OF LIFE . . . . . . . . . . . . . . . . . . . . 63
3. WHOLENESS AND THE THEORY OF CENTERS . . . . . . . . . . 79
4. HOW LIFE COMES FROM WHOLENESS . . . . . . . . . . . . 109
5. FIFTEEN FUNDAMENTAL PROPERTIES . . . . . . . . . . . . 143
6. THE FIFTEEN PROPERTIES IN NATURE . . . . . . . . . . . . 243

PART TWO

7. THE PERSONAL NATURE OF ORDER . . . . . . . . . . . . . 299
8. THE MIRROR OF THE SELF . . . . . . . . . . . . . . . . 313
9. BEYOND DESCARTES: A NEW FORM OF SCIENTIFIC OBSERVATION . . 351
10. THE IMPACT OF LIVING STRUCTURE ON HUMAN LIFE . . . . . . 371
11. THE AWAKENING OF SPACE . . . . . . . . . . . . . . . . 403

CONCLUSION . . . . . . . . . . . . . . . . . . . . . . . . 441

APPENDICES: MATHEMATICAL ASPECTS OF WHOLENESS AND LIVING STRUCTURE . . 445

BOOK TWO: THE PROCESS OF CREATING LIFE

PREFACE: ON PROCESS . . . . . . . . . . . . . . . . . . . . . . . . . . 1

PART ONE: STRUCTURE-PRESERVING TRANSFORMATIONS

1. THE PRINCIPLE OF UNFOLDING WHOLENESS . . . . . .. . . . . . . . 15
2. STRUCTURE-PRESERVING TRANSFORMATIONS . . . . . . . . . . . . . 51
3. STRUCTURE-PRESERVING TRANSFORMATIONS IN TRADITIONAL SOCIETY .. . 79
4. STRUCTURE-DESTROYING TRANSFORMATIONS IN MODERN SOCIETY . . . . . . 101

INTERLUDE

5. LIVING PROCESS IN THE MODERN ERA: TWENTIETH-CENTURY CASES WHERE LIVING PROCESS DID OCCUR . . . . . . . . . . . 131

PART TWO: LIVING PROCESSES

6. GENERATED STRUCTURES . . . . . . . . . . . . . . . . . . 169
7. A FUNDAMENTAL DIFFERENTIATING PROCESS . . . . . . . . . . . . . . . . 193
8. STEP-BY-STEP ADAPTATION . . . . . . . . . . . 217
9. ALWAYS HELPING TO ENHANCE THE WHOLE. . . . . . . . . . . . . 237
10. ALWAYS MAKING CENTERS . . . . . . . . . . . . . . 253
11. THE SEQUENCE OF UNFOLDING . . . . . . . . . . . . 287
12. EVERY PART UNIQUE . . . . . . . . . . . 311
13. PATTERNS: RULES FOR MAKING CENTERS . . . . . . . . . . . 329
14. DEEP FEELING . . . . . . . . . . . 357
15. EMERGENCE OF FORMAL GEOMETRY . . . . . . . . . . 387
16. FORM LANGUAGE . . . . . . . . . . . . . . . 415
17. SIMPLICITY . . . . . . . . . . . . . 439

PART THREE: A NEW PARADIGM FOR PROCESS IN SOCIETY

18. THE CHARACTER OF PROCESS IN SOCIETY . . . . . . .. . . . . . . . 473
19. MASSIVE PROCESS DIFFICULTIES . . . . . . . . . . . . . . . 489
20. THE SPREAD OF LIVING PROCESSES THROUGHOUT SOCIETY . . . . . . 511
21. THE ARCHITECT IN THE THIRD MILLENIUM . . . . . . . . . . . 531

CONCLUSION . . . . . . . . . . . . . 541

APPENDIX: AN EXAMPLE OF A LIVING PROCESS: BUILDING A HOUSE . . . . . . 547

BOOK THREE: A VISION OF A LIVING WORLD

PREFACE: THE FUNDAMENTAL PROCESS REPEATED TEN MILLION TIMES . . . 1

PART ONE

1. OUR BELONGING TO THE WORLD: PART ONE. . . . . . . . . . 21
2. OUR BELONGING TO THE WORLD: PART TWO . . . . . . . . . 39

PART TWO

3. THE HULLS OF PUBLIC SPACE . . . . . . . . . . . . . . 65
4. THE FORM OF PUBLIC BUILDINGS . . . . . . . . . . . 99
5. PRODUCTION OF GIANT PROJECTS . . . . . . . . . . . 147
6. THE POSITIVE PATTERN OF SPACE AND VOLUME IN THREE DIMENSIONS ON THE LAND. . . . . . . . . . . 165
7. POSITIVE SPACE IN STRUCTURE AND MATERIALS . . . . . . 199
8. THE CHARACTER OF GARDENS . . . . . . . . . . . . . 239

PART THREE

9. FORMING A COLLECTIVE VISION FOR A NEIGHBORHOOD . . . . . 267
10. RECONSTRUCTION OF AN URBAN NEIGHBORHOOD . . . . . . 291
11. HIGH DENSITY HOUSING . . . . . . . . . . . . . . . 323
12. FURTHER DYNAMICS OF A GROWING NEIGHBORHOOD . . . . . 343

PART FOUR

13. THE UNIQUENESS OF PEOPLE’S INDIVIDUAL WORLDS . . . . . 365
14. THE CHARACTER OF ROOMS . . . . . . . . . . . . . 405

PART FIVE

15. CONSTRUCTION ELEMENTS AS LIVING CENTERS . . . . . . 439
16. ALL BUILDING AS MAKING . . . . . . . . . . . . . 473
17. ACTIVE INVENTION OF NEW BUILDING TECHNIQUES . . . . 507

PART SIX

18. ORNAMENT AS A PART OF ALL UNFOLDING . . . . . . 543
19. COLOR WHICH UNFOLDS FROM THE CONFIGURATION . . . . 577

EPILOGUE: THE MORPHOLOGY OF LIVING ARCHITECTURE ARCHETYPAL FORM: . . . . . . . . . . . . . . . . . . . 601

CONCLUSION: THE WORLD CREATED AND TRANSFORMED . . . . 637

BOOK FOUR: THE LUMINOUS GROUND

PREFACE: TOWARDS A NEW CONCEPTION OF THE NATURE OF MATTER . . . I

PART ONE

1. OUR PRESENT PICTURE OF THE UNIVERSE . . . . . . . . . . . 11
2. CLUES FROM THE HISTORY OF ART. . . . . . . . 29
3. THE EXISTENCE OF AN "I" . . . . . . . . . . 49
4. THE TEN THOUSAND BEINGS. . . . . . . 73
5. THE PRACTICAL MATTER OF FORGING A LIVING CENTER. . . . . . . . . . . 111 MID-BOOK APPENDIX: RECAPITULATION OF THE ARGUMENT. . . . . . . . . 135

PART TWO

6. THE BLAZING ONE . . . . . . . . . . . 145
7. COLOR AND INNER LIGHT. . . . . . . . 157
8. THE GOAL OF TEARS . . . . . . . 241
9. MAKING WHOLENESS HEALS THE MAKER. . . . . . . . . . . . . 261
10. PLEASING YOURSELF . . . . . . . . . . . . . . . . . . 271
11. THE FACE OF GOD . . . . . .. . . . . . . . . . . 301

CONCLUSION TO THE FOUR BOOKS

A MODIFIED PICTURE OF THE UNIVERSE . . . . . .. . . . 317 EPILOGUE: EMPIRICAL CERTAINTY AND ENDURING DOUBT . . . . . . . . 339 ACKNOWLEDGEMENTS . . . . . . . . . .. . . . . . . . . . 347

DEDICATION

I DEDICATE THESE FOUR BOOKS TO MY FAMILY:

TO MY BELOVED MOTHER, WHO DIED MANY YEARS AGO;

TO MY DEAR FATHER, WHO HAS ALWAYS HELPED ME AND INSPIRED ME;

TO MY DARLINGS LILY AND SOPHIE;

AND TO MY DEAR WIFE PAMELA WHO GAVE THEM TO ME,

AND WHO SHARES THEM WITH ME.

THESE BOOKS ARE A SUMMARY OF WHAT I HAVE UNDERSTOOD ABOUT

THE WORLD IN THE SIXTY-THIRD YEAR OF MY LIFE.

THE PHENOMENON OF LIFE

PROLOGUE TO BOOKS I-4: THE ART OF BUILDING AND THE NATURE OF THE UNIVERSE

The activity we call building creates the physical order of the world, constantly, unendingly, day after day. In the last five millennia, human beings have created millions upon millions of cubic yards of building, and millions of buildings, houses, roads, and cities — entire worlds. Our world is dominated by the order we create.

But although we are responsible for the creation of order on this enormous scale, we hardly even know what the word "order" means. Our present idea of "order" is obscure. Although the word is often used informally by artists and biologists and physicists — usually to stand for some deep regularity we cannot quite define — we need a better understanding of the deep geometric reality of order. If we are honest we must admit we hardly even know what kind of phenomenon it is. Yet we build the world, producing its order, day by day. Thus we go on, willy-nilly creating order in the world, without knowing what it is, why we are doing it, what its significance might be.

In physics and biology some progress has been made toward understanding the phenomenon of order, and the processes which create order. The creation of living organisms through the morphogenetic process, the creation of matter, the creation of stars and galaxies from nuclear fire, the constant creation of particles by interaction with one another — have all been studied in the last seventy years. In these limited cases we now have

a rudimentary idea of the way the order-creation works. It has become clear, too, that the way the order is created in these cases is of essential importance to our understanding of the world. Our knowledge of order-creating processes in physics, chemistry, and biology has molded the modern view of the universe.

The art of building has not, so far, had a comparable impact on our understanding of the world. Our modern picture of the universe, what kind of stuff space and matter is made of, has not been influenced by building or by architecture. Yet, I shall argue, the process of building is an order-creating process of no less importance than those of physics and biology. It is vast in its scale and scope. It is almost universal in our experience. It is therefore reasonable to think that the art of building might give us equally essential insights.

In what follows I shall try to show that there is a way of understanding order which is general and does do justice to the nature of building and of architecture. It is a view which, I hope, is adequate to understanding the intuitions we have about beauty and the life of buildings. It is a view which tells us what it means for a building to be a great building, and when a building is working properly. It is, I believe, a common-sense and powerful view, with practical results.

If you accept the view of order I am proposing, you will find it has unexpected intellectual

results. It modifies our view of the physical universe and the way the universe is put together. Thus, what starts out as a way of understanding architecture ends up, also, as a view which may affect our understanding of physics and biology. When we understand the art of building from this point of view of order, it not only changes our understanding of the building process, but also has the capacity to change our cosmology.

I did not start out as a philosopher, and I have no special desire to write about philosophy or about the nature of things. This is not my trade. I am interested in one question above all—how to make beautiful buildings. But I am interested only in real beauty. I was never interested in making the kinds of slick buildings which architects of my time have generally been making. They have, in many cases, given up the making of real beauty—and have, by implication, even given it up as an attainable ideal. This is perhaps understandable. Making buildings at the level of beauty which was common in 12th- or 15th-century Europe and in hundreds of other cultures in almost all eras of human history except our own is very hard for us. It was especially hard for us, in the late 20th century, and will continue to be as we enter the 21st. For some reason—not at first entirely clear to me thirty-five years ago—it is a matter of such difficulty for us that architects have almost given it up. But I have not been willing to do so. I never agreed to put up with second best, or to accept the almost silly idea of “good architecture” which certain 20th-century architects have foisted on the public. I wanted to be able to do the real thing—and for that I had to know what the real thing is. The reason was not intellectual curiosity—but only the practical reason that I wanted to be able to do it myself.

Thinking about these matters has been extremely difficult. It has taken me thirty-five years to think my way out of the intellectual thicket where I started. And I believe this intellectual confusion is shared today by almost every architect. I am at heart a very empirical person. I try to think carefully about things, and I want them

to make sense. Again and again I found that there are issues in the making of buildings where our modern mentality—our way of looking at the world—makes it hard, or impossible, to come to grips with the facts as they really are.

Issues which were straightforward in other ages—such as spirit, for example, or the life that can exist in stone—are inadmissible for us. I found it almost unbearablely difficult to accept some of the theoretical concepts I was led to in the course of my work on these topics. Yet the problems we must face if we are to make things beautiful kept me coming, again and again, to fundamental questions about the nature of matter, and about the nature of the empiricist tradition—especially the tradition which we ascribe to René Descartes.

As a scientist trained in mathematics at Trinity College, Cambridge, I found that I was sometimes formulating concepts which were hard to believe. Sometimes I felt I was betraying my training. The new principles I discovered seemed questionable. It was, in many cases, even embarrassing to formulate them, very hard to allow myself to think these thoughts. I stood looking always at my empiricist tradition, and at the tradition of thought which I learned at Cambridge, and felt ashamed sometimes to be saying such things. But the facts I encountered were stronger than my squeamishness. I found that I was able to construct a coherent view of order, one which deals honestly with the nature of beauty, but only by formulating new and surprising concepts about the nature of space and matter. In the end, it was my respect for empirical truth that made me give up my doubts, and gave me the strength to formulate conceptions which are—for an empiricist of 20th-century training—suspicious or potentially ridiculous.

Even now, on some days I look at the theory I have formulated in these four books and can hardly believe that it is true. It provides a view of the universe which is so surprising, and so much at odds with the normal common-sense ways of thinking about physical reality we have currently, that it seems almost like a fantasy, like

some kind of science fiction. But then, on other days, I go through the arguments again and realize that no matter how strange these ideas are, it is hard to avoid the conclusion that they must be true. There seems to be no alternative way of putting things together — at least not one that I have been able to discover — in which we get a proper view of the things that are important.

Skeptical readers will share my doubt about the intellectual formulations I have presented. Some of the formulations will seem very hard indeed to swallow. But for that very reason, and since it is above all the skeptical reader whom I would like to persuade, I express my own doubt about what I have done, and confess to a squeamishness which must be at least as great, perhaps even greater, than that of the most skeptical reader. Yet in the end I do believe that what I have written here is true.

As a child I was always impressed by Saint Teresa. She was a 16th-century Spanish Carmelite nun who — so history tells us — was made a saint not because she believed so intensely in God, but because of her doubt. Most of the time she did not believe in God. Only now and then she did believe. But she never gave up her struggle and her doubt. She struggled with her faith, and, in the midst of her doubt and disbelief, found occasionally for a few moments that indeed she did believe. For this she was canonized.

I have always identified with Saint Teresa. Her confusion and her honesty seem very typical of our own age. Much of the time I find myself wondering if the theory I have presented in this book can really be true, or if I have merely concocted some fantastic fiction. But occasionally, in a few lucid moments, I see clearly, and it seems to me that it must be true, simply because there is no other explanation which is equally convincing and covers all the facts. Then in another instant I am doubting again, because it is just too difficult for a hard-boiled empiricist like me to believe that the metaphysical part, especially, of what I have written, and my analysis of the nature of space and matter, really can be true.

A few years ago, I was asked to go to the premiere of a film which had been made about my work. I was reluctant to go. It was a weekend, and I wanted to be with my family. In the end, though, we all decided to go together, Pamela and Lily and Sophie and I. The film was being shown at a film festival in San Francisco, at an old movie-house in the Mission district. We went in, they were showing all kinds of art films and new films one after the other, mainly fairly short ones. We sat through several of these films. Then mine came along, half an hour long. When the lights went up, I stood up. I had been asked to come forward and answer some questions.

To my surprise people started cheering. I was astonished. Of course touched, very moved. But to be honest I couldn't quite understand the reason for it. Of course I liked it. But anyway, it still seemed inexplicable.

I walked up to the stage, and people kept cheering and clapping. When I got there, the lights were very bright. They began asking questions, I gave not very good answers, the lights were so bright. We went along for a few minutes like that.

Then someone asked me, How did you come up with the pattern language? How did you get the actual material?

I said, "Well, it was not so very different from any other kind of science. My colleagues and I made observations, looked to see what worked, studied it, tried to distill out the essentials, and wrote them down."

"But," I went on, "we did do one thing differently. We assumed from the beginning that everything was based on the real nature of human feeling and — this is the unusual part — that human feeling is mostly the same, mostly the same from person to person, mostly the same in every person. Of course there is that part of human feeling where we are all different. Each of us has our idiosyncrasies, our unique individual human character. That is the part people most often concentrate on when they are talking about feelings, and comparing feelings. But that idiosyn-

cratic part is really only about ten percent of the feelings which we feel. Ninety percent of our feelings is stuff in which we are all the same and we feel the same things. So, from the very beginning, when we made the pattern language, we concentrated on that fact, and concentrated on that part of human experience and feeling where our feeling is all the same. That is what the pattern language is—a record of that stuff in us, which belongs to the ninety percent of our feeling, where our feelings are all the same.”

When I said this, a sort of cry went up, people shouted and clapped again, stood up and cheered. Then dimly I began to understand why they had been clapping when I first came forward. What they saw in me was a voice saying that our shared human feeling has been forgotten, hidden in the mess of opinion and personal differences. What people find, and what moves them, in all the work which my colleagues and I have been doing for so many years, is that we have tried to honor and respect the reality of this huge ocean—this ninety percent of our self—in which our feelings are all alike. The fact that this huge basis, this huge ocean, has been forgotten—and has, perhaps, in my own works been reawakened—that is what brought them there that day to see that film, that is what made them stand up and shout.

This book, at root, is about the core of that ninety percent of our feeling which we all share. It is about a more realistic conception of the world and of the universe which comes into existence—and can come into existence—only when we acknowledge that to a very large degree we are all the same.

I should perhaps say a brief word about my claim that these four books are “an essay on the art of building and the nature of the universe.” In the course of explaining my views on architecture, and what it takes to make a coherent architecture, I have proposed models that include two features which would be large enough to justify the claim that these books are about the nature of the universe.

One of these is the claim that all space and matter, organic or inorganic, has some degree of life in it, and that matter/space is more alive or less alive according to its structure and arrangement. This claim is discussed in the present volume, Book I, THE PHENOMENON OF LIFE. The other is the claim that all matter/space has some degree of “self” in it, and that this self, or anyway some aspect of the personal, is something which infuses all matter/space, and everything we know as matter but now think to be mechanical. This claim is discussed in Book 4, THE LUMINOUS GROUND.

If either of these claims comes, in future, to be considered true, that would radically change our picture of the universe. Indeed, one might then say that the universe as we have known it for the last four hundred years, even in the exciting and fascinating versions of physics and cosmology which have come under discussion in recent decades, would then have to be replaced by a fundamentally different and more personal view of matter.

PREFACE

1 / OUR CONFUSION IN ARCHITECTURE

In the 20th century we have passed through a unique period, one in which architecture as a discipline has been in a state that is almost unimaginably bad. Sometimes I think of it as a mass psychosis of unprecedented dimension, in which the people of earth—in large numbers and in almost all contemporary societies—have created a form of architecture which is against life, insane, image-ridden, hollow. The ugliness which has been created in the cities of the world, and the banality and pretentiousness of many 20th-century buildings, streets, and parking lots have overwhelmed the earth. Much of this construction is caused by developers, housing authorities, owners of hotels, motels, airport authorities. In that sense architects might be considered blameless, since in some degree the ugliness of what has been created is caused by new relations between time, money, labor, and materials and by a set of conditions in which the real thing—authentic architecture that has deep feeling and true worth—is almost impossible.

But architects are not blameless. For the most part, architects have stood by, content to play their role as part of the 20th-century machine. In many cases they make it worse. They gild the lily of commercial development with pretentiousness. Many architects have raised the designer-conscious fashion of building to new levels, have invented absurd ways of thinking about architecture, have altogether poisoned the earth with an abundance of terrible and senseless designs which have few redeeming features.

Of course there are many architects who struggle to make socially useful architecture. Low-cost housing, shelters for homeless people, communities and pedestrian neighborhoods, better apartment buildings, offices set in green landscapes and parks. But somehow these, too, often fail to hit the mark. The intellectual satisfaction of these sincere goals is rarely matched by a true feeling of value achieved, of buildings, streets, and neighborhoods which are nourishing and which act as fitting vehicles for our sacred human life.

In traditional society, building was almost always something that stood for human value, that raised life to its greatest possible heights, that supported a spiritual and meaningful conception of human existence.

Now, instead, too many architects rub their hands cynically, foisting images on the public, creating works which are not friendly to people, or to the human spirit, but are friendly to the developers who make huge profits from these buildings and which do much to bolster those architects with financially rewarding glossy images in magazines.

Of course architects, like others, have a conscience. Many of us regret the situation. Many struggle, like drowning men and women, in the sea that engulfs us. Some of us, though, do not know what to do. We must eat, we cannot afford to lose our jobs. The conditions which create the inhumane architecture that is being produced cannot be too closely scrutinized, since too close a scrutiny can lead to uncomfortable questions, which may ultimately make us unemployable. So, in one form or another, we — all of us, architects, builders, planners, and financiers, who have taken part in the construction of the modern environment — have participated, willy-nilly, and for the most part with little more than mild objection to this robbing of the earth.

That is what I mean by a mass psychosis. Has there ever been a time in the history of the earth when a group of people, entrusted by society with the creation and preservation of our physical world, have so sadly undermined it, become collaborators with the enemy—when the enemy is, even, unknown to many of us? Is there even an enemy at all? Yet we have, many of us, parlayed our own profession to a new con-

dition in which it not only follows this madness, but even leads others on, continues it, protects it, enlarges it.

I do not think architects are happy with all of this, any more than other members of society are happy. In the last two decades voices have begun to be heard. People have written, spoken out. Away with the emperor's new clothes! We can all see that he is naked. Let us not go on with these charades.

What is it that has to be done? How should an architect who feels that things are wrong set them right? Many of us know that something is wrong, and yet do not know, concretely, how to act to correct the wrong. How is it possible to improve the situation, when the process that causes so much destruction is so deeply rooted in society that it is almost impossible for one architect, or even a hundred architects, to stand up against it and have any positive effect?

2 / HOW ARCHITECTURE DEPENDS ON OUR PICTURE OF THE WORLD

Very few people realize, I think, how much the present confusion which exists in the field of architecture is wound up with our conception of the universe.

I have come to believe that architecture is so agonizingly disturbed because we—the architects of our time—are struggling with a conception of the world, a world-picture, that essentially makes it impossible to make buildings well. I believe this problem goes so deep that it even makes it extremely difficult to build the most modest, useful building in an ordinary way.

Many of us are not especially aware that our conception of things—our picture of the universe—could have any concrete or immediate effect on our activity as architects. We go about our business trying our best to make good buildings—in whatever fashion we understand "good." The task is difficult. We struggle with it. But we are not aware, I think, that our effort is affected in any substantial way by the picture we have of things, the picture we have of the world. Most of us are not even aware, perhaps, that we have any special picture of the world.

And, if we do ever carefully examine our own picture of the world, we shall find, no doubt, a rather complicated mixture of things: vague conceptions of atoms, galaxies, and stars; organic life as it appears on earth from, we are told, some primordial soup of amino acids. Mixed with this, there is no doubt some form of concern for our fellow human beings, some kind of piety, some awareness that certain things are more beautiful and others less. How can all this muddled mess of a conception of the world be responsible for anything?

How could it possibly be true that this conception might interfere so deeply with our efforts as builders, that it makes it all but impossible to make a building well?

The implication seems fantastic. And yet this is just what I believe. I believe that we have in us a residue of a world-picture which is essentially mechanical in nature—what we might call the mechanist-rationalist world-picture. Whether or not we believe that we are subscribing to this picture, whether or not we are aware of the impact of its residue in us, even when we consider ourselves moved by spiritual or ecological concerns, most of us are still—I believe—to a greater or lesser extent in the grip of some residue of this mechanical world-picture. Like an infection it has entered us, it affects our actions, it affects our morals, it affects our sense of beauty. It controls the way we think when we try to make buildings and—in my view—it

has made the making of beautiful buildings all but impossible.

What exactly do I mean by the mechanistrationalist picture of the world? What I mean, roughly, is the 19th-century picture of physics. That is, a picture of a world made of atoms which whirl around in a mechanical fashion: a world in which it is assumed that all the universe is a blind mechanism, whirling on its way, under the impact of the "laws of nature." These laws are, essentially, those mechanistic laws which explain how the atoms and the structures made of these atoms proceed on their way, under the influence of forces and configurations. Coupled with this picture there is a larger picture of weather, climate, agriculture, animal life, society, economics, ecology, medicine, politics, administration, and even family life — all understood in a more or less mechanical fashion. Even though we would admit that the precise laws and mechanisms may not be known, we assume that underlying our ignorance there are some laws, not quite formulated, which do account for how things work, even in these everyday surroundings. Thus we carry forward a blithe and rather simple mental assurance that it is all created by the pushing and pulling of events, very much the way we also understand the pushing and pulling of 19th-century atoms.

Of course, there are relatively few people alive today who wholeheartedly believe that the world really is such a place. Physicists—especially the great physicists—have a more humble and wondering attitude about the nature of the universe. So do many non-scientists. Architects are, at least explicitly, rarely concerned with such a mechanistic picture. On the surface architects appear to be concerned with deeper questions—artistic and social questions—that are often more mysterious and more interesting.

However, in trying to probe the nature of the puzzle surrounding the collapse of architecture, I have slowly become convinced that many architects—especially those who have become

famous in recent years and whose work now forms the model for the work of younger architects—are in the grip of such a mechanistic conception, even if they do not know it. I have reached the conclusion that the strange fantasies, the private in-house language about architecture, the strange nature of 20th-century gallery art, deconstructionism, postmodernism, modernism, and a host of other "isms," all of which affect our physical world hugely, are created because of an entanglement between the nature of architecture, the practice of architecture, and the mechanical conception of the universe.

Thus, I believe that there is, at the root of our trouble in the sphere of art and architecture, a fundamental mistake caused by a certain conception of the nature of matter, the nature of the universe. More precisely, I believe that the mistake and confusion in our picture of the art of building has come from our conception of what matter is.

The present conception of matter, and the opposing one which I shall try to put in its place, may both be summarized by the nature of order. Our idea of matter is essentially governed by our idea of order. What matter is, is governed by our idea of how space can be arranged; and that in turn is governed by our idea of how orderly arrangement in space creates matter. So it is the nature of order which lies at the root of the problem of architecture. Hence the title of this book.

When we understand what order is, I believe we shall better understand what matter is and then what the universe itself is. But so long as we are—even unconsciously—prisoners of a too-simple mechanical picture of matter, it is inevitable, I am afraid, that we—and the architecture we create—must continue in the blind confusion which too many of us have experienced for more than half a century.

That is my effort in this book: to show how architecture can be made whole again, through a new picture of the nature of order, and through a new picture of the nature of matter itself.

3 / WHAT IS ORDER?

What is order? We know that everything in the world around us is governed by an immense orderliness. We experience order every time we take a walk. The grass, the sky, the leaves on the trees, the flowing water in the river, the windows in the houses along the street — all of it is immensely orderly. It is this order which makes us gasp when we take our walk. It is the changing arrangement of the sky, the clouds, the flowers, leaves, the faces around us, the dazzling geometrical coherence, together with its meaning in our minds. But this geometry which means so much, which makes us feel the presence of order so clearly — we do not have a language for it.

And what should we do to create order? Even the smallest building has order of great complexity. In the course of laying out and making the volume of the building, the filigree of structure, floors, windows, doors, and ornament — we face a dazzling task. What is the order we should infuse it with? In large projects, especially, we can easily get muddled. More is at stake, so the nature of the order we put in is especially crucial. We rely more on intellectual conceptions. So then, our assumptions about order begin to enter in explicitly. It is not only a single brick, or door, or roof. It might be a whole neighborhood — millions of dollars of construc

tion — perhaps the living environment for hundreds of people at a time. How do I do this? What kind of order should it embody, to make sure it is a success?

In facing any one of these tasks, I come up against this question right away: What exactly do I mean by order? If I want to get an idea of order which is deep enough to be really helpful—helpful to me, helpful to my craftsmen, helpful to my students, helpful to my clients, helpful to my apprentices and my staff—I have to define exactly what I mean by order.

In a sense, everyone knows what order is. But when I really ask myself “what is order”—in the sense of deep geometric reality, deep enough so that I can use it, and so that it is able to help me create life in a building—then it turns out that this “order” is very difficult to define.

Look at the yellow tower on the facing page. It has the smile of the Buddha, of life and simplicity. It moves us in the heart. I want a conception of order subtle enough to explain the way the yellow tower makes us feel. The conceptions of order which physics currently defines, and most other current ideas of order, are simply inadequate for a profound task like this.

Scientists have been trying to define order for about a century. The idea of order as a precise concept first entered physics as a by-product of thermodynamics, when the orderliness of molecules in a perfect gas was analyzed numerically by Ludwig Boltzmann in 1872 through the idea of entropy. Unfortunately the order which can be treated as negative entropy is too simple, and, for complex artistic cases, almost trivial.¹ In the 20th century, the hunger of the scientific community for some precise concept of order was so great that attempts to extend the notion of thermodynamic order to cover all order were made by many writers outside the field of physics.² Sober generalizations of the thermodynamic concept of order were also made by physicists.³ None of this went far enough to be helpful to artists.⁴

What other ideas of order can we get from modern physics? We could concentrate on special types of order like crystallographic order, defined by repetition.⁵ But this concept is too limited to be much help in making something subtle and beautiful. We could develop conceptions of military or hierarchic order. These too have been analyzed, but are too limited to be much help.⁶ Complex patterns generated by interacting rules are more interesting, and raise the possibility of seeing all order as the product of a computable generative process.⁷ This could give us a general view of order as any system produced by interacting generative morphological rules.⁸ In other cases of this type we have an orderly pattern-making process based on the interaction of rules which can simulate the motion of a thrown ball, or a breaking wave. Still more complex, we are beginning to have some idea of biological order, an order of a growing thing in which one system unfolds continuously to form another.⁹ In recent years, biologists have tried to formulate more sophisticated concepts of order.¹⁰ Unfortunately, these attempts have also not yielded results which are practically useful in the art of building.

Deeper theories of order have been attempted. A preliminary sketch of a very much deeper theory was once made by the physicist Lancelot Whyte, who tried to develop a view of all biology as a science of asymmetrical ordered structures.¹¹ The theory of catastrophes, which tries to describe the birth of configurations out of chaos, has been developing in recent years and is considered by many to be promising.¹² Perhaps one of the clearest statements so far has been expressed by the physicist David Bohm. Bohm tried to outline a possible theory in which order types of many levels exist and are built out of hierarchies of progressively more complex order types.¹³

But none of this, suggestive as it all is, is directly useful to a builder. Even the most advanced of these ideas is still not deep enough or concrete enough to give us practical help with architecture, where we actually try to create order every day. If I want to build a building as beautiful as the yellow tower, these theories of order

are not even remotely deep enough to help me in a practical fashion. None of these theories are even capable of helping us to understand the order of the yellow tower.

Look at the other examples of buildings on pages 12-13. Each has some kind of profound order. But within our present limited worldview we cannot describe this order scientifically. Do we even understand what their makers were trying to do? The beautiful smooth columns from Ise have an immensely subtle order, where a few ropes and small pieces of white cloth utterly change the building. The tomb of Timur has a magnificence which comes from its high body, and the fluting on the dome. These buildings move us, and touch us in our hearts. In a more modern form, the steel base of the Palm House at the Berlin Botanical Garden has a similar quality. The steel plates and bolts are very harmonious, perfectly sized. It feels like

the bones of an animal. The glass and ironwork roof of the London arcade has a similar, completely naturalistic quality. And the small drinking cup, a simple piece of cut bamboo, leaves my heart pure and quiet.

For contrast, on page 14 there are a few examples of more recent buildings. They also have order of some sort; but they are less gentle: they do not go to the heart; they are less beautiful. The apartments in Amsterdam have a brutal repetition which has little to do with the organic order of human life. The fake arches of Frank Lloyd Wright's Marin County Civic Center in California are purely decorative: they have little to do with the profound sense of order we feel in something that is structurally real. The bank building of white stucco is uninteresting and oversimplified. Its order, insofar as there is any, is certainly not one which reflects the actual beauty and subtlety of a large build-

ing, or of a complex human group. Eero Saarinen's war memorial building in Minneapolis is gross, brutal, and appalling.

Are these intuitions objectively verifiable? Is there actually less order in these later examples than in the earlier examples? Or is it just a different order?

We feel the difference in order between the examples on pages 12–13 and the examples on page 14. But can we understand this difference objectively? Are these apparently crude examples really more crude than the other examples? Is the order of the Ise shrine, or of the tomb of Timur the Great, genuinely and objectively more profound than the repetition of the Amsterdam apartments? What, indeed, is that thing we intuitively feel as order in all these different cases?

It is extraordinary to realize that, in the current intellectual context, not one of these questions has had a clear answer.¹⁴ Among current ideas of order, there is no conception of

order which helps us create the profound life that can exist in buildings and in other artifacts.

Of course, today, as a matter of practice, when we try to make a building we usually ignore this problem. We know that what physics has to say about order isn't enough, and we use our intuition to try and get the order of the building right. But this weak and only mechanical view of order is unlikely to go on working in the intellectual climate of the 21st century. It is not only the particular kinds of order that occur in physics that are inadequate. Every idea of order, even our intuitive and artistic ideas of order, are inadequate because they are, in my view, based on a wrongheaded foundation. It is the whole idea of order, the whole idea of what order is, as it exists in 20th-century thought, which is inadequate.

And for making things, or giving life to them, our current ideas of order are utterly inadequate.

4 / ORDER AS MECHANISM

In the 20th century, we have had the illusion that all the order we see around us in the world can be explained by science — mainly, we assume, by physics. But physics and the other sciences tend to represent certain things for us as mechanisms. This gives us a partial picture of some kinds of order. That is all. We may take, for instance, the structure of a leaf, the structure of a bridge, the structure of an atomic nucleus. In each of these cases we have a well-worked-out conception of the mechanical order which is there. The stems of the leaf support its membranes, which hold the cells, which receive sunlight, and transform the energy of the sunlight into materials from which the leaf can grow. The members of the bridge are conceived as elements in a certain pattern of forces which develops inside the bridge in response to a given pattern of loads, trucks and cars passing over it, wind forces, stresses and strains caused by thermal expansion, and so on. Even in the picture we have of the atomic nucleus, the order is conceived essentially in relation to forces. The particles of which the atom is made are themselves seen as carriers of forces which hold the nucleus together and which, under particular conditions, may also cause it to fly apart.

What is the order which physics helps us talk about in each of these cases? It is only the mechanical order. The order is always described—and even invented—in relation to the way the thing works as a mechanism. Within our current scientific world-picture, each of the three examples I have given is conceived of as a little machine that produces certain kinds of results when pushed, prodded, squeezed, or bombarded. So, in the present scientific world-picture, the order which we see in the thing, the way we describe it to ourselves, is essentially the order of a machine which has a certain mechanical mode of operation—or which, at any rate, has a certain kind of mechanical behavior as a result of the arrangement of its parts.

But what of the order itself? The order itself—that order which exists in a leaf, in the Ise shrine, in the yellow tower, or in a Mozart symphony, or in a beautiful tea bowl—a harmonious coherence which fills us and touches us—this order cannot be represented as a mechanism. Yet it is this harmony, this aspect of order, which impresses us and moves us when we see it in the world.

It is almost impossible to view a Mozart symphony as a machine which has certain kinds of behavior. The same is true of the yellow tower. If, as an artist, I want to understand the tower—if I want to make something of comparable beauty—it is useless to conceive it as a mechanism, because the beauty and order which I see in it, and yearn for, cannot be expressed in any way that can be understood mechanically. So, in works of art, the mechanistic view of order always makes us miss the essential thing. Although 20th-century science gives us a way of seeing order as a producer of effects—in particular because the scientific view of things shows us the geometry of matter as if it were part of a machine, a machine which can do certain things—we still do not have a way of seeing the order of a thing which simply exists. We do not have a way of seeing the order in the smile of a statue of the Buddha, or in the exact position of a flower in a vase, or of the arrangement of notes in a song, or of the harmony within a wonderful building.[15]

5 / DESCARTES

The mechanistic idea of order can be traced to Descartes, around 1640. His idea was: if you want to know how something works, you can find out by pretending that it is a machine. You completely isolate the thing you are interested in — the rolling of a ball, the falling of an apple, the flowing of the blood in the human body — from everything else, and you invent a mechanical model, a mental toy, which obeys certain rules, and which will then replicate the behavior of the thing. It was because of this kind of Cartesian thought that one was able to find out how things work in the modern sense.¹⁶

However, the crucial thing which Descartes understood very well, but which we most often forget, is that this process is only a method. This business of isolating things, breaking them into fragments, and of making machinelike pictures (or models) of how things work, is not how reality actually is. It is a convenient mental exercise, something we do to reality, in order to understand it.

Descartes himself clearly understood his procedure as a mental trick. He was a religious person who would have been horrified to find out that people in the 20th century began to think that reality itself is actually like this. But in the years since Descartes lived, as his idea gathered momentum, and people found out that you really could find out how the bloodstream works, or how the stars are born, by seeing them as machines — and after people had used the idea to find out almost everything mechanical about the world from the 17th to the 20th centuries — then, sometime in the 20th century, people shifted into a new mental state that began treating reality as if this mechanical picture really were the nature of things, as if everything really were a machine.

For the purpose of discussion, in what follows, I shall refer to this as the 20th-century mechanistic viewpoint. The appearance of this 20th-century mechanistic view had two tremendous consequences, both devastating for artists. The first was that the “I” went out of our world-picture. The picture of the world as a machine doesn’t have an “I” in it. The “I,” what it means to be a person, the inner experience of being a person, just isn’t part of this picture. Of course, it is still there in our experience. But it isn’t part of the picture we have of how things are. So what happens? How can you make something which has no “I” in it, when the whole process of making anything comes from the “I”? The process of trying to be an artist in a world which has no sensible notion of “I” and no natural way that the personal inner life can be part of our picture of things — leaves the art of building in a vacuum. You just cannot make sense of it.

The second devastating thing that happened with the onset of the 20th-century mechanistic world-picture was that clear understanding about value went out of the world. The picture of the world we have from physics, because it is built only out of mental machines, no longer has any definite feeling of value in it: value has become sidelined as a matter of opinion, not intrinsic to the nature of the world at all.

And with these two developments, the idea of order fell apart. The mechanistic idea tells us very little about the deep order we feel intuitively to be in the world. Yet it is just this deep order which is our main concern.

The real nature of this deep order hinges on a simple and fundamental question: “What kinds of statements do we recognize as being true or false?” This is the question which divides the mechanistic world-view originating with Descartes from the one which I describe in this book.

In the world-view initiated by Descartes — and largely accepted by scientists in the 20th century — it is believed that the only statements

which can be true or false are statements about mechanisms. These are the so-called "facts" familiar to everyone in the 20th century.

In the world-view I am presenting, a second kind of statement is also considered capable of being true or false. These are statements about relative degree of life, degree of harmony, or degree of wholeness — in short, statements about value. In the view I hold, these statements about relative wholeness are also factual, and are the essential statements. They play a more fundamental role than statements about mechanisms. It is for this reason that the view of order which I am presenting in this book inevitably involves us in a shift of world-view.

Suppose I am trying to place a door in a certain wall. While I try to decide where to put it, I can make various mechanical statements of fact. For example, I can say of one door that it is wide enough to allow a refrigerator through it, that it will resist a standard fire for one hour, that it weighs 25 kilograms, and so on. I can also make more elaborate statements of fact. In one case people can see through the door, in another they can't. I can even say that the position of one door may disrupt people's work because their desks are too exposed to the noise of passers-by. I might have to do an experiment to check this statement, but it is still, in principle, a statement of fact in the normal Cartesian sense. All these statements are, potentially, statements of fact in the 20th-century mode. This is the sense in which the word "fact" is understood today. It is generally agreed that statements of this type may be true or false.

But if I am trying to put the door in the wall, there is also a second kind of statement about the different possible positions for the door. For example: "When the door is in a certain range of positions, the result is more harmonious than other positions." "This position for the door is more in keeping with the wholeness of the room than this other position." "One door frame is more harmonious and more in keeping with the life of the room than another door frame." "One door creates more life in the room

than another door." "A pale yellow on this door has more life than a dark gray." Within the canon of 20th-century science, these are not considered statements which can be true or false. They are thought of as statements of opinion. As a matter of principle within the 20th-century mechanistic view, statements of this kind may not be considered potentially true or false.

We have learned to live with this principle simply because we are used to it. But consider how bizarre it really is. As architects, builders, and artists, we are called upon constantly—every moment of the working day—to make judgments about relative harmony. We are constantly trying to make decisions about what is better and what is worse in an evolving building. If the only statements considered potentially true or false are mechanistic statements of fact, and if all statements of harmony, beauty, what is better or worse, what has more life or less life, are always considered matters of opinion which can only be referred to private and arbitrary canons of judgment—then, in principle, rational discussion about buildings should be impossible.

The devastating impact of this state of affairs on the progress of architecture has not, I think, been sufficiently discussed in recent decades. Within a world-view in which statements about value are not allowed, by the accepted canon, to be considered as potentially true or false, we cannot (in theory) legitimately discuss what we are doing as architects with any hope of reaching consensus. If we accept the 20th-century idea that statements of value are — of necessity — merely statements of opinion, it is in principle impossible to reach any sensible shared conclusion in the process of making the environment — only arbitrary and private conclusions. The chaos with which we are familiar in the built world, must then follow as an inevitable conclusion — as indeed it has.

Discussion of an earlier book may perhaps help to make the problem clear. In 1977 my colleagues and I published a book called A PATTERN LANGUAGE.[17] In this book we made a number of observations about good environments. The

book was—and still is—extremely controversial. It describes a number of key patterns in cities, buildings, gardens, and building details which are necessary to support life. Some people said that it described an important form of truth. Others said it was impossible for the book to describe any form of truth and that it was only opinion dressed up as truth.

According to the strict canon of contemporary science, it would indeed be impossible for statements about "good" patterns to be true since they do not have the right logical form to be true. In the present-day scientific canon patterns in the pattern language must be statements of opinion. And some writers, working within the Cartesian-mechanistic mental framework, indeed took this point of view.[18]

However, after the book was published, many hundreds of other people came to the conclusion that the statements in the pattern language are not statements of opinion but are in some sense true. Since the patterns seem to confirm people's instincts about what is true in the environment, to these people, who were not

committed to the mechanistic canon, the patterns represented a triumph of deeper wisdom reflecting common sense.[19]

What are we to make of this? It suggests, I think, that there must be some other way not covered by the limited mechanistic idea of what can and cannot be true, in which statements about value can be true. And indeed, this is the main philosophical assumption which underlies the arguments of the present book.

Throughout this book I shall present a further and more extended idea of objective truth—one which extends the current idea of truth given us by 19th- and 20th-century science in such a way that it includes statements of value. As I hope to show, this new extended idea of truth is not only objective, but is also directly linked to people's feelings. Most importantly, this extended idea of objective truth will allow statements about relative harmony, wholeness, and so forth to be judged as true or not true. In this view, these kinds of statements are not left as private intuitive opinions or agendas, but describe the structure of things in the world as they are.

6 / THE DESTRUCTIVE IMPACT OF MECHANISTIC THOUGHT ON THE ART OF BUILDING

It is not a small thing to construct a theory of architecture based on a new form of truth. To make sure the reader understands—thoroughly—why I believe it is necessary for us to develop a new form of truth, I shall give a few more examples of the highly negative impact the mechanistic idea of truth has had on the art and architecture of the 20th century.

In the architecture of the last decades, constructive discussion about value has become difficult—sometimes nearly impossible. In the wake of the mechanistic world-picture, we have constructed a pluralist view of value. When we want to discuss the pros and cons of a particular action—in architecture, planning, landscape—

each person is understood to have a "view," or attitude, or value-orientation. There is rarely any theoretically coherent way of combining different people's values. So, if it is a public matter, we simply give each person the opportunity to express his point of view as strongly as possible, in the hope that the ensuing democratic dialogue will somehow get us to a balance point roughly in the middle.

And this is indeed what happens in 20th-century discussion of building projects, planning, and the actions which may arise in any public situation. In discussing what to do in a particular part of a town, one person thinks poverty is the most important thing. Another person thinks ecology is the most important thing. An-

other person takes traffic as his point of departure. Another person views the maximization of profit from development as the guiding factor. All these points of view are understood to be individual, legitimate, and inherently in conflict. It is assumed that there is no unitary view through which these many realities can be combined. They simply get slugged out in the marketplace, or in the public forum.

But instead of lucid insight, instead of growing communal awareness of what should be done in a building, or in a park, even on a tiny park bench—in short, of what is good—the situation remains one in which several dissimilar and incompatible points of view are at war in some poorly understood balancing act.

Our zoth-century failure to construct a living world arises necessarily from this situation. Since, in the mechanistic framework, the different values brought to architecture are inherently inconsistent, architects quite contentedly take the confusion of their many individual, wildly different, and inconsistent ways of thinking as the basic situation which must exist in architecture. Consciously or unconsciously, the architect assumes that only "factual" statements (in the mechanistic sense) can be true, and therefore has it as a further (unconscious) assumption

that the idea of what is good is something that you add to the factual statements—something that is (of necessity in the current scientific world-view) only a matter of opinion.

All this sounds abstract. But its impact on our world has been enormous. It has created a mental climate of arbitrariness, and has laid the foundation for an architecture of absurdity.

For example, a few years ago a man came to show me a design he had drawn for a building. The building was to be made entirely of oil-drums filled with water. It was intended to be an energy-efficient building. Yet the building was absurd in many ways. It was ugly, impractical, hard to build, not even pleasant to be near. But it made sense to him because, as far as he was concerned, he was only trying to make an energy-efficient building. He had chosen this particular goal, and elevated it above all others, making it the basis for his work.

To Buckminster Fuller, weight was paramount. He therefore emphasized the idea of least-weight structures. It didn't matter to him that a geodesic dome is difficult to use, perhaps not so pleasant to look at, almost impossible to subdivide internally in a nice way. What mattered was his chosen goal of making buildings which span the longest distance for the least possible weight.[20]

Le Corbusier chose the separation of functions. With the CIAM (Congrès International de l'Architecture Moderne), he decided that housing, recreation, transportation, and work were of such importance that he chose as an underpinning value the task of giving these four functions adequate and separate space in the city. In the process, he may have had to forget

about the interweaving of other functions—but it was this goal of separating the four functions, above all others, which dominated his city plans. This was his chosen value, and this is what he reflected in his diagram of the Radiant City.[21]

More recently we have examples of architects who choose historical reference as the primary value in their work. Look, for instance, at the neo-classical facade on this page. In this case it might not matter whether the building works well or not: what matters is that it has a certain "image"—perhaps the image of Palladio mixed with images of the 1940s. This architect chose this particular goal—the making of an image—above all others.

Another architect may choose to make wildly formal geometric shapes on the grounds that they are "good design." There is no empirical basis for believing that this is true. But again, in the absence of believable empirical facts about what is true or not, one must choose something. So, a one-sided belief that crystalline geometric forms have an absolute goodness can provide yet another architect with the underpinning for his work: as in the Rotterdam offices contained in rhombic crystals which I show on the facing page.

Architects make different idiosyncratic choices because within the mechanistic worldview it is not possible to function mentally without making some private choices of this kind. Virtually every architect who works today is forced to do something similar. Yet another architect is an adherent of ecology. He seeks to preserve nature. But how should this be done? In fire-prone brushland above the Berkeley hills, should the land be cleared of trees and brush to protect it against fire? Should it be made into a useful park, thus leaving the trees for shade? Should it be left messy and wild to preserve the habitat of the native birds and plants (a biologist's point of view)? Should it be left as it is simply to save money (the university's point of view)? Should it be wild, or tamed? Once again, within the mechanistic framework, it is simply a matter of

opinion. You take your pick between the opposing viewpoints. Although these points of view do not have quite the insane arbitrariness of the more extreme architectural examples I have given, still each point of view that can be expressed is still essentially arbitrary: whether one of them is chosen, or some combination of them, any particular choice is individual, and arbitrary again.

So far the 20th-century response to the arbitrariness inherent in mechanistic thought has been to keep on asserting the dignity and privacy of value. Something like this: "Science only tells us about facts. When it comes to figuring out what one ought to do, that is a private matter of art or ethics. It is your natural right to work out your own values. Not only will our scientific world-view not tell you anything about value,

it is your democratic obligation to do it for yourself."

But all this only continues to make the "life" of towns and buildings and landscapes seem unreal, almost as if it did not exist. It also makes cooperative work, collaboration, and social agreement very difficult in principle. It has a superficial permissiveness which seems to encourage different opinions. But what is encouraged, really, is only the essential arbitrariness of ideas rooted in a mechanical view of how the world is made.

What we need is a sharable point of view, in which the many factors influencing the environment can coexist coherently, so that we can work together—not by confrontation and argument—but because we share a single holistic view of the unitary goal of life.

7 / A NEW VISION OF ARCHITECTURE

To achieve this aim — to make buildings which have life and profound order — it is necessary to be rescued from the mechanistic trap by concentrating on the life and order of a building as something in itself.²² I believe such a formulation can only come from a new view of the world which intentionally sees things in their wholeness, not as parts or fragments — and which recognizes “life,” even in an apparently inanimate thing like a building, as something real.

In this new view of order we shall find, necessarily, a post-Cartesian and non-mechanistic idea of what kinds of statements can be true, a theory in which statements about relative degree of harmony, or life, or wholeness — basic aspects of order — are understood as potentially true or false. This means we shall have a view of the world in which the relative degree of life of different wholes is a commonplace and crucial way of talking about things.

Such a new view of order will create a new relationship between ideas of ornament and function. In present views of architectural order, function is something we can understand intellectually; it can be analyzed through the Cartesian mechanistic canon. Ornament, on the other hand, is something we may like, but cannot understand intellectually. One is serious, the other frivolous. Ornament and function are therefore cut off from each other. There is no conception of order which lets us see buildings as both functional and ornamental at the same time.

The view of order which I describe in this book is very different. It is even-handed with regard to ornament and function. Order is profoundly functional and profoundly ornamental. There is no difference between ornamental order and functional order. We learn to see that while they seem different, they are really only different aspects of a single kind of order.

What is even more important, we shall see that the structure I identify as the foundation

of all order is also personal.²³ As we learn to understand it, we shall see that our own feeling, the feeling of what it is to be a person, rooted, happy, alive in oneself, straightforward, and ordinary, is itself inextricably connected with order. Thus order is not remote from our humanity. It is that stuff which goes to the very heart of human experience. We resolve the Cartesian dilemma, and make a view of order in which objective reality “out there” and our personal reality “in here” are thoroughly connected.

In forming this idea of order, we shall have to take intellectual steps which touch all of science — even physics and biology — because we need to include a new view of what statements can be true or false. The life of a building will become visible as something empirically real. We shall see that the yellow tower and other buildings in the first group of examples in this chapter empirically have more life than the modernistic buildings in the second group of examples. This will become objectively clear not as a matter of opinion, but as a matter of fact about the order they contain.

The theory which I shall lay out is in no sense against science; it is simply an extension of science. Like all science, it will show a view of things which depends on clearly defined structures: but structures which show us order in new ways, not available to present-day scientific thought. What will be presented is a slightly modified vision of science, which includes mechanism as understood in the past, but also includes a powerful new kind of structure, coupled with a new form of observation, that transforms the range and extent of the experiences which science can illuminate.

The new view will show us the world as an altogether different kind of place from the one we have imagined. When we are done, everything will look different, not only buildings.

Flowers, puddles, waterfalls, bridges, mountains, the moon, the earth, the tides, the waves of the ocean, paintings, the rooms in which we live, the clothes we wear—all of these will be different in our eyes and will appear to us as something fresh and marvelous. We shall, then, literally, be living in a different mental universe.

At that stage we shall not only have a concrete grasp of order as a single phenomenon which affects all of architecture, but shall also be led to a view of space and substance which is transcendental. Although this conception of order is lucid in material terms, it will also provide us with a partial understanding of the nature of

matter which reaches beyond our present material view of substance, and beckons to some domain beyond the limits of space and time.

Thus it is not only the detail of what "order" is which needs to be questioned, but also the very nature of order.[24] So long as we have a confused or inaccurate conception of what kind of thing order is, we shall inevitably make buildings which are ugly, houses which do not support ordinary human well-being, gardens and streets which are at odds with nature, and a world which destroys our souls.

To make good architecture, we must fundamentally alter our idea about the nature of order — about the kind of thing it is.

NOTES

1. Negative entropy measures the unlikelihood of a configuration of particles. It can account for low-level order in aggregates of molecules, but not for any complex order which is interesting in art or architecture — nor indeed can it deal with complex order in physics or biology.
2. Including Fred Attneave, APPLICATIONS OF INFORMATION THEORY TO PSYCHOLOGY: A SUMMARY OF

BASIC CONCEPTS, METHODS, AND RESULTS (New York: Holt, Rinehart & Winston, 1959); W. R. Garner, UNCERTAINTY AND STRUCTURE AS PSYCHOLOGICAL CONCEPTS (New York: John Wiley & Sons, 1962); and others. 3. For example Purcell, "Order and Magnetism," in PARTS AND WHOLES, Daniel Lerner, ed. (New York: The Free Press of Glencoe, 1963).

4. Indeed, the feeble nature of this first attempt, and its comparative uselessness for art, was carefully analyzed by Rudolph Arnheim, ENTROPY AND ART (Berkeley: University of California Press, 1971).

5. The successful analysis of the crystal groups was vital, but extremely limited in its scope. Andreas Speiser, THEORY OF GROUPS OF FINITE ORDER (Berlin: J. Springer, 1937).

6. See, for example, Albert G. Wilson and Donna Wilson, eds., HIERARCHICAL STRUCTURES (New York: American Elsevier Publishing Company, Inc., 1969).

7. H. Eugene Stanley, "Fractals and Multifractals: The Interplay of Physics and Geometry," in Armin Bunde and Shlomo Havlin, eds., FRACTALS AND DISORDERED SYSTEMS (Berlin: Springer-Verlag, 1991).

8. Structural grammars of the kind first defined by Chomsky are special cases of this kind of order. For instance, Noam Chomsky, STRUCTURAL LINGUISTICS (The Hague: Mouton, 1959).

9. Turing's early theory of morphogenesis might be looked at like this. A. M. Turing, "The Chemical Basis of Morphogenesis," in PHILOSOPHICAL TRANSACTIONS OF THE ROYAL SOCIETY, B (London, 1952), pp. 237 ff.

10. For example, André Lwoff, BIOLOGICAL ORDER (Cambridge, Mass.: MIT Press, 1965); C. S. Waddington, THE STRATEGY OF THE GENES: A DISCUSSION OF SOME ASPECTS OF THEORETICAL BIOLOGY (London: Allen and Unwin, 1957).

11. L. L. Whyte, THE UNITARY PRINCIPLE IN PHYSICS AND BIOLOGY (New York: Henry Holt and Co., 1949) and L. L. Whyte, ACCENT ON FORM (New York: Harper & Brothers, 1954).

12. René Thom, STABILITÉ STRUCTURELLE ET MORPHOGÉNÈSE (Paris: Christian Bourgeois, 1972) and James Gleick, CHAOS: MAKING A NEW SCIENCE (New York: Viking, 1987).

13. David Bohm, "Remarks on the Notion of Order," and "Further Remarks on the Notion of Order," in C. H. Waddington, ed., TOWARDS A THEORETICAL BIOLOGY: 2. SKETCHES (Chicago: Aldine Publishing, 1976).

14. An account of artistic order was tried by Ernst Gombrich in ORDER AND ART (London: Allen and Unwin, 1977), but in this book order still appears as something additional, pasted on top of whatever else art produces. The concepts are still only barely useful for an artist.

15. The progressive mechanization of our modern world-picture was exhaustively described by E. J. Dijksterhuis, THE MECHANIZATION OF THE WORLD PICTURE (Amsterdam: Meulenhoff, 1959; translated and reprinted, Princeton, N.J.: Princeton University Press, 1986). It is also the main theme of Alexandre Koyré's FROM THE CLOSED WORLD TO THE INFINITE UNIVERSE (Baltimore, Md.: Johns Hopkins University Press, 1957) which ends with these words: "The infinite Universe of the New Cosmology, infinite in Duration as well as Extension, in which eternal matter in accordance with eternal and necessary laws moves endlessly and aimlessly in eternal space, inherited all the ontological attributes of Divinity. Yet only those — all the others the departed God took away with Him."

16. The essence of mechanistic theory is that the machine is governed only by local effects: by actions which are, strictly speaking, pushing and pulling. There is no "action at a distance," and above all, the whole has no way of influencing the parts. In 17th-century physics (Newton) there was some action at a distance: gravity. In 19th- and early 20th-century physics there was some action at a distance, in the field effects of electricity, light, and so on. The late 20th century has been marked by an exorcism of action at a distance, and by now electromagnetic fields, quantum theory, even the working of Hamilton's function and the principle of least action are all described as far as possible in terms of local effects. See for instance Richard Feynman, QED (Princeton, N.J.: Princeton University Press, 1985).

17. Christopher Alexander, Sara Ishikawa, Murray Silverstein, Ingrid King, Shlomo Angel, and Max Jacobson, A PATTERN LANGUAGE (New York: Oxford University Press, 1977).

18. For example, Jean Pierre Protzen, "The Poverty of the Pattern Language," CONCRETE: JOURNAL OF THE STUDENTS IN THE DEPARTMENT OF ARCHITECTURE, Part one: vol. 1, no. 6, November 1, 1977; Part two: vol. 1, no. 8, November 15, 1977, University of California, Berkeley; reprinted in DESIGN STUDIES, vol. 1, no. 5 (London, July 1980), pp. 291-98.

19. Reviewers expressing this point of view published their comments in many dozens of articles written since 1975. A strong example by Stewart Brand appeared in THE WHOLE EARTH CATALOG (Sausalito, Calif.: Doubleday, 1980-90).

20. Buckminster Fuller, "The Long Distance Trending in Pre-Assembly," IDEAS AND INTEGRITIES: A SPONTANEOUS AUTOBIOGRAPHICAL DISCLOSURE, ed. R. W. Marks (Englewood Cliffs, N.J.: Prentice-Hall, 1963).

21. Le Corbusier, THE RADIANT CITY, Pamela Knight and Eleanor Levieux, trans. (New York: Orion Press, 1967).

22. The idea that order may exist as a fundamental, not machine-like, idea has become visible in some parts of 20th-century physics. One of the first examples was Pauli's exclusion principle (Wolfgang Pauli, "Exclusion Principle and Quantum Mechanics," COLLECTED SCIENTIFIC PAPERS, vol. 2, R. Kronig and V. F. Weisskopf, eds. (New York: John Wiley and Sons, 1964): a pure property of arrangement was shown to govern the behavior and position of electrons, without being caused by the action of a force or mechanism, but purely as a result of pattern and order in themselves.

23. See chapters 8-11 of this book, and Book 4, throughout.

24. The possibility that the order observed in science and the order created in art might ultimately be treated as one phenomenon has been mentioned by many writers, starting with Goethe. In recent writings, see for example, György Kepes, THE NEW LANDSCAPE IN ART AND SCIENCE (Chicago: Theobald, 1956); Hermann Hesse, DAS GLASPERLENSPIEL (Zürich, 1943); Christopher Alexander, "The Bead Game Conjecture," in ORDER AND ART, György Kepes, ed., (New York: Braziller, 1967).

What is living structure?

What is life in buildings?

What is a living world?

What is the structure of a living world?

CHAPTER ONE: THE PHENOMENON OF LIFE

1 / INTRODUCTION

It is widely agreed today that we want to build towns and buildings which play their proper role in the preservation and continuation of life on earth. This has come about, in large part, as a result of the growing interest in ecology. When we study ecology, we begin with the idea that we must preserve nature, preserve the rain forest and chaparral, preserve the animals and plants of the earth. This general desire to preserve living things is then extended to tell us that we should build buildings and towns and neighborhoods, in such a way that their action also plays its role in the balanced harmony and life of the earth.

At first the effort to make buildings play their proper part in the living system of nature was seen as a narrow problem, which meant that one's use of energy, use of materials, use of resources, should all be consistent with the preservation of the earth as a balanced living system. More recently this interest has expanded. Many people now define their aim to be the creation of towns and buildings which are part of the living fabric of the earth and which are themselves, in short, alive.¹

But here, suddenly, we find ourselves up against a very unusual scientific problem. Within biological sciences as they stand at the end of the 20th century, we do not have a useful, or precise, or adequate definition of "life." In traditional 20th-century scientific orthodoxy, life—or, to be more precise, a living system—has been defined as a special kind of mechanism. The word "life" has been applied only to a certain limited system of phenomena. We shall see, in this book, that this conception of things needs to be changed. "Order" may be understood as a most general system of mathematical structures that arises because of the nature of space. And "life," too, is a concept of comparable generality. Indeed, in the scheme of things I shall describe, every form of "order" has some degree of "life."

Thus life is not a limited mechanical concept which applies to self-reproducing biological machines. It is a quality which inheres in space itself, and applies to every brick, every stone, every person, every physical structure of any kind at all, that appears in space. Each thing has its life.

The need for a broader view of life comes about, in a simple way, from the ecological viewpoint. Nowadays many people have begun to recognize the importance of animals, plants, and living systems to the earth; and have begun to seek a view of architecture and city planning which is consistent with the maintenance of life. So far this has been fairly intuitive. It has meant that, in addition to buildings, architects want to create systems of trees and plants which sustain themselves: systems of building that are wholesome with respect to nature, coordinated with natural processes, not damaging to the great forests of the Amazon, not damaging to the birds and butterflies in the backyard. For several decades architects and lay people have understood this form of architecture as something desirable.

But we need to push the ecological idea further. What it needs—what it already has, as a seed within it—is a conception of life which goes beyond the narrow mechanistic biological view of life, and somehow embraces all things.

This arises from the desire to take everything as a single system and to make it whole. If we want to take an ecological view of architecture, we naturally try to take the view that our job on earth is to create life in buildings and in towns, not only in the "wild" part of nature. This is quite different from merely preserving the natural life which exists. It means creating life in man-made things and natural things together.

Southern England, for example, is one of the largest structures ever made by man. We think of it as nature: the beautiful expanse of towns, villages, fields, forests and moors that

extends from Cornwall to Kent, and from the south coast to the Midlands. We think of it as natural, but of course it is man-made, almost all of it. It wasn't there three thousand years ago. It is a consciously created structure, perhaps 300 miles by 100 miles, and it has been created slowly, patiently, over a period of about a thousand years. The fields, ditches, copses, hedges, streets, cow-paths, streams, ponds, bridges, and villages are something which includes nature, which has the same life that we attribute to nature. But it was made by man.

This active creation of a non-natural structure which clearly has life, and which is alive, is very much more than merely preserving nature. It is much harder, to begin with, because it has to be invented; it is not a case of merely smiling at nature and saying, "Let's keep it that way." The fact that it is even possible poses enormous intellectual difficulties. In order to understand it, grasp it mentally, and to do

it, we must have a conception of things in which the relation between living tissue, in the narrow biological sense, and non-living matter (again, non-living in the narrow biological sense), can be made clear and understood. We must not only want the bush to be alive with respect to birds, earth, rain, and so on, but we must also understand how the piece of wood in the windowsill, the piece of concrete in the edge of the flower bed fit into this pattern of life and complete it. Thus we are after one pattern of life, which includes the so-called living organisms and the so-called dead matter in a single living system. It is a case of understanding the interaction of man and nature, and making a harmony out of that interaction, which has the beauty of nature and the zest of life. The making of such a structure has been done repeatedly in different cultures during different ages: the Japanese house and garden, the terraced hillsides in

China and the Himalayas, the building of Machu Picchu, the creation of the medieval landscape, the relation of the Cheyenne Indians to the plains where they placed their tepees.

These cases are excellent models for us as we struggle both with ecological catastrophes and a man-made world which is ugly, aggressive, and non-life-supporting.

2 / THE NEED FOR A BROADER AND MORE ADEQUATE DEFINITION OF LIFE

So far we do not have a definition of life which clearly applies to these larger and more complex systems. In the 20th-century scientific conception, what we meant by life was defined chiefly by the life of an individual organism. We consider as an organism any carbon-oxygen-hydrogen-nitrogen system which is capable of reproducing itself, healing itself, and remaining stable for some particular lifetime. This definition is not so easy to pin down perfectly. There are plenty of uncomfortable boundary problems: For example, is a fertilized egg alive during its first few minutes? Is a virus alive? Is a forest alive (as a whole, and over and above the life of the component species taken as individuals)? Are carbon, hydrogen, oxygen, nitrogen necessary to what we shall define as life?

Even though riddled with logical holes and awkward questions, still in broad terms it is the life of the individual organism which gives us the basis of what we consider alive, and what we define as "life," in the late 20th century. We have, it is true, begun some extrapolations of this idea of life, and have started trying to apply them to more complex systems. For example, we have somehow managed to extend the mechanical concept of life to cover ecological systems (even though strictly speaking an ecological system is not alive, because it does not meet the definition of a self-replicating organism). We consider an ecological system as a system of organisms, and therefore, though not alive itself, certainly associated with biological life. The task of creating or conserving the natural world can therefore be understood, in precise terms, as

an effort to increase the organic life in a particular part of the world, and this has partially reasonable scientific meaning.

But this extrapolation will not do to help us understand truly complex systems as living things. The mixture of natural and man-made which exists in any city or any building—or in the huge 300-mile-long structure of southern England—raises complicated questions of definition, which we have hardly begun to answer. In all these cases we have obviously non-living systems mixed in with the living systems: for example, the rafters of a house, the roof tiles, the road, the bridge, the gate; even the furrows in the field. In normal scientific parlance, one could not possibly call these things alive. And yet clearly they do have a vital role in the overall life of the larger systems. If we adhere to the purely mechanistic picture of life, we are stuck with preservationist adherence to ecological nature in its purest form—just as ecological purists have in fact been stuck with the idea that they must keep nature "as it is," because this is the only way they can define clearly what they want to do. The moment we want to treat the more complex system of buildings and nature together, as one living system, we run into intellectual problems because we no longer have an adequate scientific definition of what we are trying to do. For example, according to present-day biological terminology, a city is not a living system, even though it is often referred to as a living system by social scientists in search of a metaphor. Obviously, too, a building is not a living system. How can we try to make a living system out of a region, or a city, or a build-

ing — even out of a garden — when, according to current scientific orthodoxy, these things are not living systems?

Throughout this book, I shall be looking for a broad conception of life, in which each thing — regardless of what it is — has some degree of life.² Each stone, rafter, and piece of concrete has some degree of life. The particular degree of life which occurs in organisms will then be seen as merely a special case of a broader conception of life. Although this may sound absurd to ears trained in the last few decades of scientific orthodoxy, I shall try to show that this conception is more profound scientifically, that it has a solid basis in mathematical and physical understanding of space, and above all that it does provide us with a single coherent conception of the world, and of what we are doing in the world, when we try to make the world “alive.”

In the present scientific world-view, a scientist would not be willing to consider a wave breaking on the shore as a living system. If I say to her that this breaking wave does have some life, the biologist will admonish me and say, “I suppose you mean that the wave contains many micro-organisms, and perhaps a couple of crabs, and that therefore it is a living system.” But that is not what I mean at all. What I mean is that the wave itself—the system which in present-day science we have considered as a purely mechanical hydrodynamical system of moving water—has some degree of life. And what I mean, in general, is that every single part of the matter-space continuum has life in some degree, with some parts having very much less, and others having very much more.

It is not hard to see that such a conception — if we could get it — would make it much

easier to design buildings, towns, and regions. If the conception of life is completely general, we shall then be able to extend it from the purely natural (such as conservation of a beautiful stand of trees), to the cooperation between natural and man-made (roads, streets, gardens, fields), and then also to the buildings themselves (roofs, walls, windows, rooms). In such a mental world, it will become easy to make sense of architecture — because we can then simply proceed with the general idea that all our work has to do with the creation of life and that the task, in any particular project, is to make the building come to life as much as possible.

3 / A NEW CONCEPT OF “LIFE”

My aim in this book is to create a scientific view of the world in which this concept — the idea that everything has its degree of life — is well-defined.³ We can then ask very precise questions about what must be done to create life in the world — whether in a single room, even in a doorknob, or in a neighborhood, or in a vast region, where, as the English people of southern England did once long ago, we might again create life in large parts of California, or Asia, or indeed in any region of the world.

As a background for our work, I shall in this first chapter simply try to persuade you, by example, that we do feel that there are different degrees of life in things — and that this feeling is rather strongly shared by almost everyone.

Let us first consider the breaking wave. When we see waves in the sea, we do certainly feel that they have a kind of life. We feel their life as a real thing, they move us. Of course, in the narrow mechanistic view of biology there is no life in the wave (except insofar as it has seaweed or plankton living in it). But it is undeniable — at least as far as our feeling is concerned — that such a moving, breaking wave feels as if it has more life as a system of water than an industrial pool stinking with chemicals. So does the ripple on a tranquil pond.

It is also clear that one lake feels more alive than another — a clear crystal mountain lake, for instance, compared with a stagnant pond which feels more dead. A fire, which is not organically alive, feels alive. And a blazing bonfire may feel more alive than a smoldering ember. The moons of Jupiter, if you have ever seen them through a telescope, feel alive, like four liquid droplets of light. They feel alive to an uncanny degree. Yet, in conventional terms they are not.

Gold feels alive. The peculiar yellow color of naturally occurring gold, so different from pyrites, or from the gold in the jeweller’s shop, has an eerie magic essence that feels alive. This is not because of its monetary value. It got its monetary value originally because it had this profound feeling attached to it. Naturally occurring platinum, comparable in value, or rhodium, which is far more valuable, do not have the same feeling of life at all.

Marble, too, sometimes feels alive. The quarries at Carrara, in Italy, are famous because the marble from that place feels intensely alive. Another marble may feel more ornate but less alive. Artificial marble — polymerized stone dust — as it might appear in a bathroom counter in Las Vegas, feels much less alive. Yet none of the three is actually alive, biologically.

We often see a piece of wood and marvel at its life; another piece of wood feels more dead. Of course, you may say that the wood was once alive. But again, in the exact biological sense, it is certainly not alive now. Yet we do feel that the grain of one piece has more life than another.

Thus, throughout the world of non-organic physical systems, we make distinctions. We recognize cases which seem to have a great deal of life, others which seem to have none, others in

between. The intuition, or impression, of life exists in a wide variety of physical systems.

We shall see later that this feeling that there is more life in one case than the other is correlated with a structural difference in the things themselves—a difference which can be made precise, and measured. But for now, I merely want to record the intuition that some different physical systems appear to have more feeling of

life and others less feeling of life. Obviously this does not prove that this intuition is anything more than a subjective perception. But it does at least open the door a crack, to the possibility that there might be some kind of real structural phenomenon behind the feeling. All I hope to do, so far, is to encourage the reader to begin thinking that this might not be merely a metaphor, or an anthropocentric view.

4 / THE FEELING OF LIFE IN ORGANISMS

When we compare different organisms we feel that some things have more life than others—even though, technically, they all have equal degrees of life. Here is a picture of a leaping cheetah. We do not need to be reminded that this animal is alive. This cheetah feels intensely alive, not just alive.

The same can happen in a meadow of flowers. Sometimes the flowers themselves have a poignancy—a lily of the valley in a misty meadow—and radiate an intense life.

We may feel the same in a person. One person may be glowing with life, which transmits to everyone around. Another person is drooping, half dead. We experience the sensation that one is more alive, and feel degrees of life in different people—even in the same person at different moments. And there are, of course, cases where a person's actual health is different. One is radiantly healthy, another less so. In this case, there may be a medical counterpart to this sensation of more life. But in any case, what is undeniable is that different organisms, all alive in the strictly mechanical sense, impress us as having more life or less life.

5 / THE FEELING OF LIFE IN ECOLOGICAL SYSTEMS

Let us go next to our most widespread experience of life—the larger life that exists in nature all around us. This is the larger "ecological" life which occurs in every natural ecosystem. It includes the well-being of a vast array of natural organisms—plants, animals, parasites, fish—which occur in and around a building. Fish-ponds, climbing

flowers, grass, mosses on the building, shade trees in the courtyards, cats, dogs, mice, insects, and spiders. In all these cases we feel the life intensely. Indeed, it is this feeling of life and love of nature which stimulated the young discipline of ecology.

On the following pages, there are two forest scenes. We see a wild profusion of organisms.

Their life is the familiar life we recognize in nature, in plants and animals, and in ourselves. Yet, as I have said earlier, there is no simple definition of life in an ecological system. Within the narrow biological definition of a living system as an organism, an ecological system as a whole is not alive. But in any case, we still experience its life. And we recognize degrees of life, or degrees of health, in different ecological systems. In recent years, we have begun to formulate technical descriptions of these ecologies which allow us to distinguish one as healthier than another.

In any case, beyond the gradual emergence of precise formulations in ecology, we do have the feeling that one meadow is more alive than another, one stream more alive than another, one forest more tranquil, more vigorous, more alive, than another dying forest.

Here again—almost regardless of what ecologists have managed, or not managed, to formulate—we experience degree of life as an essential concept which goes to the heart of our feelings about the natural world, and which nourishes us fundamentally, as a fact about the world.

6 / LIFE IN ORDINARY HUMAN EVENTS

We certainly feel different degrees of life in different human events. Consider first almost any social act. Look at the simple act of shaking hands. In one case it feels full of life; in another case, mechanical, dead.

Look at your favorite bar: a place which comes to life at night, where some special life exists, seedy, raucous. The bar. The night club. A fish-pond there. A garden seat. Shaking hands. A night at the ballet.

The "life" which I am talking about also includes the living essence of ordinary events in our everyday worlds — the fact that a back-street Japanese restaurant has life in the ordinary sense; the fact that an Italian town square comes to life in

the ordinary sense; the life of an amusement park like Coney Island; the life of a bunch of cushions thrown into a corner window-seat — any building where we feel alive; a place where wildflowers grow comfortably; a place where people are free to talk and eat and drink and be themselves. I have described this very ordinary but intensely living quality of buildings and places in the first few chapters of THE TIMELESS WAY OF BUILDING. This quality includes an overall sense of functional liberation and free inner spirit. It makes us feel comfortable. Above all it makes us feel alive when we experience it. I add pictures of a few examples here, so that we have an image in mind of what this "ordinary" life is all about, both what it

really means and what it looks like, as a structure, when it occurs. Like biological life, it has a typical appearance. It is rather rough, not manicured. It is comfortable, rough around the edges, smooth as if it has been rubbed together. This kind of life is the ordinary life which is not connected to high art or fashion. It has nothing to do with images. It occurs most deeply when things are simply going well, when we are having a good time, or when we are experiencing joy or sorrow — when we experience the real.

The freedom which arises when life is at its most spiritual, and also most ordinary, arises just when we are "drunk in God," as the Sufis say—

most blithe and most unfettered. Under these circumstances, we are free of our concepts, able to react directly to the circumstance we encounter, and least constrained by affectations, concepts, and ideas. This is the central teaching of Zen and all mystical religions. It is also the condition in which we are able to see the wholeness which exists around us, feel it directly, and respond to it. The association with bars is not entirely silly. Drunkenness, no doubt evil itself at times, also releases our ability to see the truth more clearly. The Romans said in vino veritas. When we have some loss of inhibition, our freedom to act and react is often truly increased.

7 / THE FEELING OF LIFE IN TRADITIONAL BUILDINGS AND WORKS OF ART

The feeling that some things live more intensely than others certainly exists in buildings, in artifacts, and in works of art. To give the reader an idea of what I mean by “the intense feeling of life” in material things, I now present a sequence of pictures which show some intense examples of this kind of life in things.

The first thing is a prehistoric Minoan vase, complex in shape and very basic, so that it hits you in the belly with its shape and with its color. The next thing, a Danish courtyard painted in yellow, red, and green, is simple and childish—but quiet and profound. The life fills you. The great mosque in Isfahan, dazzling in its color, is more magnificent. In its size, and color, it has an awe-inspiring life, somber in its reminders but, unlike a Gothic church,

bright and joyful. In contrast, a tiny Korean ceramic stand for a teapot is simple, beautifully shaped, without complication, but full in its being. Green and yellow tiles from a mosque are unconcerned, hand painted, repeating but not repeating, harmonious in their similarity, unworried in their inventiveness. A stone column capital, carved by Romanesque masons, is reused in a North African mosque. The capital is like a flower or like a person, quiet, solemn, happy. A famous Turkish prayer rug from the 15th century, now in the Berlin Museum, dazzles in the intensity of red, created by the lines, S-shapes, and by the unusual soul-like character of the prayer arch.

An archway in India: dark shadow, bright light, cool, and soul-like, the careful shaping of

the arch made so that its lobes bring life to the intense shadow and hot sunlight. A page from a 7th-century manuscript is absolutely quiet, with very little color, yet the color shines because of the skill with which the painter used it. A little yellow and brown on white produces an eerie inner light. Extreme feeling appears in a small hand-carved and painted madonna. It is small and unpretentious, yet more intense in its feeling than perhaps all the paintings of the Renaissance. The surface of a Persian bowl is brought to life by small black fly shapes, apparently painted as fast as the painter's hand could move over the surface of the inside. Another

bowl, startling in its roughness and simplicity, is the great Kizaemon tea-bowl, made in Korea, now treasured in Japan.

In every one of these examples we experience an intense feeling of life.7 We experience it in the objects themselves and in their parts. And, in keeping with the idea of order, the life we experience seems very much to lie in the geometry, in the actual geometrical arrangement of the thing.

Although we may not be able to define it exactly, I suspect that many people will agree that they see something like life in all these examples. I do not expect that we shall have perfect agreement about the examples. Still, we probably have something close to agreement.

Similarly, if we ask people for a list of the "great" buildings of the world, certain buildings will probably be mentioned: the Parthenon,

Notre Dame or Chartres, the great mosque at Isfahan, perhaps the Alhambra, perhaps the Ise shrine or one of the earliest Buddhist temples in Japan, like Tofuku-ji. The very existence of this list suggests the measure of agreement which lies behind it.

And this agreement about life in things extends to lesser examples. The early Christian churches in Rome, the Norwegian stave churches, the mosque at Kairouan, the ruins at Palenque or Ixtlan, Machu Picchu in Peru, the long huts of the Sepik river people in New Guinea, the small tiled houses of Morocco, the great barn houses of northern Germany and Denmark, the arcades of Bologna, the bridge at Isfahan.

In only slightly lesser measure than the most famous examples, these, too, while less

imposing, have an ability to touch us, to make us feel still, awed when we are in them, silent, grateful. There is not much doubt about their greatness. And people will generally agree that all these things have life in them—in some degree—though, again, just what this life is, or how it might be defined, perhaps remains unclear.

The quality I call life in these buildings exists as a quality. It is clearly not the same as the biological life we recognize in organisms. It is a larger idea, and a more general one. Indeed, what we intuitively feel as "life" in these objects happens just as much in a purely abstract thing like a painting as it does in a functioning thing like a building, or in a biologically living system like a tree.[7]

It is this very general life — formal, geometric, structural, social, biological, and holistic — which is my main target. It includes the profound life of the geometric structure that we have seen in historical examples (their plaster, concrete and tile, the life of their colors and

shapes). It includes the ordinary life, the actions and events which make us feel alive there, and which allow a happy everyday life to exist for the people and animals and plants who live there. And it includes the biological life, the nurture of the natural systems which exist in and among

the buildings, so that they are biologically healthy. In a few cases, life in a thing, or in a person, or in an action, or in a building, reaches a level of intensity which is truly remarkable. This can happen in a work of art, or in a person's life, or in a moment of a day.

Above all, it does sometimes happen in buildings and in artifacts. It is this melted unity, this deepest experience of order that we experience with wonder, which is the real target of this book, since it is this quality which we are most often trying to reach when we make a building.

8 / LIFE IN TWENTIETH CENTURY BUILDINGS AND WORKS OF ART

The feeling of deep life which occurs in traditional artifacts is less common in the 20th century—especially in buildings. It is uncommon because—for reasons which will become clear throughout Book 2, THE PROCESS OF CREATING LIFE—the processes needed to create life were damaged in the 20th century.

Nevertheless, in modest degree the feeling of greater life does appear from time to time, and did appear, of course, in millions of cases during the 20th century. In the next few pages I have collected a few examples of buildings, places, and things from recent times which are ordinary enough, or profound enough, to feel alive in some degree.

In part, these examples feel alive because they are—as far as possible—concept-free.

They are not based on images, or on ideas of reality, but instead they have reality itself coming to life in them in a free way. They are vigorous and straightforward, where the soul of the maker has entered the thing—or where the ordinary process of daily life, uncontaminated by ideas or notions of what to do, has unfolded in a way that we accept very easily.

These things make us comfortable, because we recognize them as genuine. The life we feel in them comes from this genuineness. Since it is our main intention to make things which feel alive in our own time, it is these modern versions which must especially inspire us. They are the springboard from which our own efforts must come. Our own effort to form life in our time, because it must be consistent with 20th-century

life as we now find it, and as we have now created it, is the most inspiring thing of all, and our chief target.

To produce this life, we must first see how life springs from wholeness, and indeed how life is wholeness. Wholeness exists all around us, and life springs from it. Every situation we are in, even the most mundane, has the capacity for life in it.

Comfortable ordinariness and lack of “image” quality are the main things which produce life in our current situation. A man in his shirt-sleeves, a cafe which is a converted gas station, paving which is made to last a long time but also

to honor small plants without being precious, machines in a workshop, the decoration on a giant trucking rig, a hammock which is not too new, a photograph pinned to the wall above a person's desk, paint on part of a shop window, the festive quality of a big tent with a dance for a thousand people, the loading dock of a warehouse where two people are eating a sandwich

during their lunch break in the sun. These are ordinary things which make life, even in the present environment. What we need to understand, is that this comfortable ordinariness in its thousands of manifestations, as well as the high points of modern art, are all produced by the same structure—and that, when it succeeds, this structure is "life."

9 / INTENSE LIFE IN ORDINARY POVERTY

Some of the artifacts I have shown in this chapter are very beautiful. It might be said that these things are too special, that they come from a small and privileged class of human artifacts, and that they are not representative of the vast majority of human experiences throughout the centuries of history.

But the quality of life is not precious or "high" in this sense at all. It exists also, quite easily, in the most humble and ordinary aspects of our daily lives. In this sense the great life we feel in works by Matisse and van Gogh is somewhat misleading — since the same feeling of life can occur, also, in a dirty hut or in a slum — and, indeed, is often more likely to occur in such a place than in a work of "architecture."

This is confusing, because it seems contradictory. Yet it is fundamental. Misunderstanding of this point is responsible, almost more than anything else, for our failure to produce life in modern architecture.

It is for this reason that I now show a photograph from a slum in Bangkok. The poverty and dirt allows the life to exist, allows life to shine out, because the middle-class conceptions of what is good are not at work killing the life. The conditions are so impoverished that only the direct life itself exists. Mental conceptions of what is desirable inspired by magazines, images of desire fostered by the media, here have gone out the window, or never existed.

The reader may think that I am romanticizing poverty. What about the Middle Ages, for example, with hunger, disease, and fearful human prejudice? They somehow produced better buildings than we do, at least in their cathedrals. But what about the hovels in which serfs were forced to live. Did these have life?

Yes. The answer is yes.

Of course, the disease and ignorance of these past periods are horrifying. There is nothing very lively about leprosy and starvation, which I have witnessed even in this century in an

Indian village where I lived, or in the slums of Lima.

But in the midst of all that poverty, even the shacks where people live had some direct and human quality, quite different from our own experience in a plastic tract house, or in a motel, or in a McDonald's hamburger joint. Compare the pretentious plastic-fantastic postmodern "house" on this page. It is a horrible deathly thing. Under normal circumstances this would not even be worth commenting on. But things have become so topsy-turvy in our world that this building is considered a valid work of architecture, worthy of being illustrated in architectural magazines, while the slum above is considered something terrible.

Of course it is true that the postmodern building is clean, not disease-ridden; and the people who live there probably have their health and three square meals a day. It is also true that the people who live in the Bangkok slum may have a shorter life span and may be starving. Still, even when one takes these facts into account, the place in Bangkok and the people there

perhaps have more life: while the postmodern house with its image-ridden knobs and ears perhaps has little do to with life, little to do with any deep reality.

In the slum, in some way, the direct voice of the heart is there. It is there in the mud hut of an

Indian villager, even now. It can be there even in the miserable poverty of a slum tenement in Lima. It is life, the force of direct human experience, misery, compassion, ignorance, and warmth all mixed up together. There is an honest life there. It really is life.

In the McDonald's hamburger stand of our own experience, or in the pretentious postmodern house, or in the perfect plumbing and fitted carpets of a tract house or a Tokyo apartment, we may have comfort, we may have overcome disease and found material warmth and wealth—but the direct message of the heart is often less there.

In this sense, not only the great monuments of the past, but even the hovels of the Middle Ages, even the sagging doorpost of a Tibetan village house, all have a direct contact with life, and a closeness to our own hearts, which is less present in the our environment today.⁸

10 / THE TASK OF MAKING ORDINARY LIFE IN THINGS

Let us come back now to my ordinary and commonplace effort. I want it to be possible for us — all of us — to make buildings, benches, windows, which have that simple comfort in them, so that everyone feels at home, so that they support us in our daily life.

But it turns out that this life-supporting quality, simple as it is, is also elusive. It is largely missing from the 20th century, for a variety of complex reasons. It is missing above all because some deep conceptions of matter — at first almost remote, and apparently not common-sense or practical at all — have been removed from our awareness. First among these concepts of matter is the most fundamental one — that life is a quality of space itself. Life, that very ordinary commonplace life, which we experience eating a sandwich in the sun, is something that has been removed from the intellectual landscape of our time. To bring it back again, we have to construct, carefully, a picture of the world which is adequate for these ordinary — but immensely deep — pictures of how things are.

Superficially, the many examples of life in this chapter look dissimilar. Each belongs to its own time and place. But if we examine them more deeply, there is a sense in which these different cases all look the same. They all have the same deep quality in their appearance; looking with the right eyes, one sees the same structure, again and again, in all of them.

One aspect of this structure is the "wabi-to-sabi" of Zen teaching: the Japanese concept of beauty which is best translated as "rusty beauty." These things are all beautiful, but they are all damaged. Life itself is damaged, and nothing which is perfect can be truly alive. There is a rough amiable quality in the Japanese restaurant, in the bench and the solitary watcher at Atlantic City, in the houses of the Bangkok slums, even in the blossoms of van Gogh's almond tree. This quality, the real life, the deep life of all great art, and of all genuine experience, is our aim.

The astonishing thing is that every time this very deep life shows its face, it looks the same. It looks the same in the weather-beaten face of an old man sitting by the river, it is the same in the hastily and carefully made picnic that Cartier Bresson photographed, it is the same in the quality of an ordinary natural river, it is the same in the moss along the river bank, it is the same in the loose rough repetition of boards along the side of a traditional Pennsylvania barn.

It is even the same in the very great craft and subtlety of the great Isfahan mosque and its tile-work, where the outward perfection again hides the drunkenness, the careless abandon in the individual bits of tilework that allowed the artist, drunk in self, to make a free thing in the flowers he put in the glaze.

What impresses us about all these examples is that they have a kind of blitheness or serenity,

an innocent and simple quality. Their depth is not a mechanical composition: there is a truth, an easiness, about many of these things. Their easiness takes the breath away. They arrive at a simplicity and truthfulness which ring an echo in us—sometimes perhaps even make us weak in the knees. Somehow these works remind us of the essence of life. They have a simplicity beyond artifice.⁹

The quality of life includes us, as human beings. A place which has the deepest life is one in which I reach a deeper level of life inside my self, and in my spirit. The quality of life which I attain—its depth—in any given building is part of the way I experience that building.

And it goes further. This quality of life is a pervasive one. It includes the ordinary biological life, which we usually forget when we try to judge buildings, but it also includes a kind of “life” which happens, to a lesser or a greater degree, in

the very stones, concrete, and wood posts of which the building is made. Thus it is a kind of life which is profound in a painting of apple blossoms by van Gogh, less profound in an advertising poster. It is a quality that exists in space, in every stone, in every brush-stroke, just as much as it occurs in every plant and insect, and in the ducks which walk about in my own garden in the densely populated hills of Berkeley near the University of California.

Thus it is a conception of life and architecture in which the house I live in becomes a greater thing because of the ducks in the garden—and it is a conception in which the beautiful shape of a window not only gives more life to the window, but also enlarges the window and the house.

It is, also, a conception in which my own spirit, and the spirit of each of us, is enlarged to the extent that the spirit itself has this greater

life in it — and in which the greater spirit which I reach, in my life, is inextricably connected to the presence of that life in the sticks and stones from which the building and the rooms are made.

In what follows, I hope to show that this deep and even holy conception of our lives, and of the life of our surroundings, turns out to be directly and practically connected to an identifiable structure. It is something which occurs in space. The deep order which produces life in buildings is a direct result of the physical and mathematical structure that occurs in space, something which is clear and definite, and something which can be described and understood.

NOTES

1. The points made in the first section became much more clear during a workshop which Sim Van der Ryn and I gave together at the Esalen Institute in 1991. I am very grateful to him and to the workshop members for an inspiring discussion.

2. Although such a conception does not yet exist in modern science, it does exist in traditional Buddhism, which in many sects treats the world in such a way that every single thing “has its life.” Many animistic religions too — for example, those of African tribes, or of the Australian aborigines — treat each part of the world as having its own life and its own spirit. The modern Western tradition does have a variety of half-scientific attempts — those works in the vitalist tradition, for example, by Goethe, Hans Driesch, and Henri Bergson’s CREATIVE EVOLUTION (New York: Henry Holt & Co., 1937). But these poetic accounts of the universal existence of life are not yet part of the stream of science, still not solid, structural good sense of a sort which allows us to share knowledge that holds up empirically. We do not so far have a scientific conception of this kind.

3. Theodore Roszak, THE VOICE OF THE EARTH (New York: Simon & Schuster, 1993) also describes the existence of life in all things as an emerging scientific idea.

4. According to today’s simplified definition of a self-replicating system.

5. Christopher Alexander, THE TIMELESS WAY OF BUILDING (New York: Oxford University Press, 1979), chapters 1 and 2.

6. See Aldous Huxley, THE PERENNIAL PHILOSOPHY (1945; New York: Meridian Paperbacks, 1962).

7. By 1970 a few writers had begun to comment on this quality which I have described, perhaps none more profoundly than the great Japanese potter Soetsu Yanagi, who explained his attitude in his book THE UNKNOWN CRAFTSMAN: A JAPANESE INSIGHT INTO BEAUTY (Tokyo: Kodansha International, 1972). Yanagi also founded the folk art museum of Tokyo, one of the first public institutions in modern times to honor these kinds of artifacts with proper respect. By now, this admiration and acceptance of traditional artifacts is far more widespread.

8. The fact that many examples in this chapter have a great and profound “life” may be confirmed, empirically, by simple experiments. Some of the key experiments, and variations of these experiments, are extensively described in chapters 8 and 9.

9. The general quality of life visible in these photographs (pp. 34–61) has been described by mystical writers in each of the great religious teachings. For example, by the sufts as “being drunk in God,” thus ‘Umar Ibn al-Farid, KHAMRIYYAH, c. 1235, “We have drunk to the remembrance of the Beloved a wine wherewith we were made drunk before the vine was created.” A similar theme exists in Zen art and among early Zen teachers. Among modern Western writers Hubert Benoit is one of the few to get to grips with it; see especially Hubert Benoit, THE SUPREME DOCTRINE (New York: Viking Press, 1959), translated from the French LA DOCTRINE SUPRÈME SELON LA PENSÉE ZEN (Paris: Le Courrier du Livre, 1951); also idem, LET GO (New York: Samuel Weiser, 1973). All summarized in Aldous Huxley, THE PERENNIAL PHILOSOPHY. See also “The Quality Without a Name,” in Christopher Alexander, THE TIMELESS WAY OF BUILDING, chapter 2.

CHAPTER TWO: DEGREES OF LIFE

1 / DIFFERING DEGREES OF LIFE IN OUR EVERYDAY SURROUNDINGS

The quality I have identified in chapter 1, the general beyond-biological quality of life as an attribute of all material systems, exists, I believe, to varying degrees in every part of space. It exists, for instance, in the ink and paper of the period at the end of this sentence, and it exists in the ink and paper of the letter q printed here. Of course it exists only very weakly in both, but in a slightly greater degree in the letter q than in the period. It exists in varying degrees in different human events. For instance, life exists to a greater degree in the scene from the island of Dominica, shown below on the left, than in the Harlem slum shown on the right.

In this chapter, I want to persuade the reader that almost all of us perceive this quality, and feel it as it occurs in varying degrees in different parts of space. And I want to lay the groundwork for a larger task: to persuade the reader that this quality is real. What I mean is that the different degree of life we observe in every different part of space is not merely an artifact of our cognition but is an objectively real physical phenomenon in space which our cognition detects.

I claim that this quality is not merely the basis for a distinction between beautiful things and ugly things. It is something which is detectable as a subtle distinction in every corner of the world, as we walk about, in the most ordinary places, during the most ordinary events. It is a quality which changes from place to place and from moment to moment, and which marks, in varying degrees, every moment, every event, every point in space.

In the following pairs of photographs I invite you to compare the relative degree of life in the two members of each pair. In each pair, I have put the example which seems to me to have more life on the left-hand side, and the one which seems to me to have less life on the right-hand side.

TWO PLACES IN POVERTY: ONE MORE ALIVE, ONE MUCH MORE DEAD

ROAD WITH TREES, ROAD WITH TRAFFIC LIGHTS

This example is rather obvious. The difference of life felt in these two photographs could be expressed in terms of precise biological concepts on the grounds that the one with trees has more living organisms and hence must “obviously” feel more alive. But the degree of life in other examples does not depend only on the quantity of living organisms.

ROAD WHICH IS KINDER TO THE HILLS, ROAD MORE HARSHLY CUT

The relative quantities of grass and trees visible in these two photos are roughly the same. But in the left-hand case the road is more harmoniously related to the hills — and a greater degree of life comes from this harmony. The one on the right is a little more stark, more brutal. The one on the left seems kinder to the hills, makes you more aware of the nature of the hills. It is more fun to drive on, too.

ROAD IN THE TREES, ROAD WITH OPEN HILLS

This pair is a little more puzzling. The left-hand road has more trees, more light and shade. It seems to have more life. The other has more dry grass. In this case intellectual judgment can make it hard to tell which one has more life. At first it is obvious: the left-hand example with the trees has more life. But if you start asking yourself why — there are just as many blades of grass as there are leaves on the trees, and so on — it seems to get muddled.

If, though, you don't allow yourself to think and you quickly, in two seconds, without time for thought, choose one, then you will — I believe — choose the one with the trees. The feeling is clear. Only the effort to find a theory to justify your intuition might confuse you. I believe the greater degree of life in the left-hand one has something to do with the dark and light. It is the light which has more life in the place on the left.

INSIDE THE STABLE, OUTSIDE THE STABLE

Both these places in a riding stable have industrial fixtures, bars, fences, and a person. But the one in the open has a kind of deadness about it, even though the photo is mainly focused on a man watching the horses. The interior of the barn, though darker, has a more comfortable quality, and is less stark. In this pair, one may start to see that the feeling of life we experience in different places can be a subtle matter and that we may have to consult our feelings carefully to get clear about it.

MORE FRIENDLY HOUSE EDGE, LESS FRIENDLY HOUSE EDGE

In this case perhaps it is the amount of detail, the pots of flowers, the differentiation, the comfortable completion, which brings the place on the left to life. This differentiation is mostly missing in the house on the right. The place on the left is more cared for. It has a finer grain. Perhaps this finer grain itself is responsible for the feeling that there is more life.

ORDINARY PICKUP TRUCK, ORGANIC PAINTED CAR

The "funky and organic" image is not always the one with more life. Here the painted car from California seems to symbolize life, and might therefore be chosen as more alive by an unwary reader.

But if you ask yourself which of the two actually has more life, makes you feel more in touch with life in yourself, has more of the truth of everyday events in it, you may then find that the pickup truck, ordinary though it is, is more genuinely in touch with life, more connected.

The organic car is more an image than it is genuinely connected to life. The pickup truck looks less inspired, but is more truly alive.

TWO VIEWS OF THE SAME BEDROOM

Here we see two different views of the same corner in a room. One focuses on the windows, and on a zone which has less life. The other focuses on the table behind the bed, and on the personal things lying there. The second, as framed, has more life.

The difference in degree is fairly obvious. But it is worth thinking about because if you are not used to making this distinction, it just may not occur to you that even within one room, one zone may be compared with another for the amount of life which each contains. In this particular case it is the zone which is more utilized because of its relation to living people, and because of the degree of adaptation and comfort that has happened there, which gives it greater life.

TWO PARKING LOTS AT THE UNIVERSITY OF CALIFORNIA

These two examples are intentionally similar in their degree of life. They lie less than fifty feet apart at the University of California. But if you ask which one has more life, and which makes you feel more alive within yourself, to look at, or to be there, you will probably choose the left-hand one. Is it the irregularity of the cars? Or the presence of the smaller scale introduced by the smaller building? It is hard to be sure of the reason, but the subtle fact remains.

GIRL IN MIRROR AND MODEL IN ADVERTISEMENT

The girl looking at herself in the mirror of a machine at Coney Island has more zest, more love of life at this moment, than the more posed model in the advertisement. In this case the one which is posed, not surprisingly, is the one which has less life.

LOBBIES OF TWO OFFICE BUILDINGS

This case is interesting. Surprisingly, the one which is more slick has more life. The left-hand lobby is slightly more polished, more slick even; and yet it has more life. It is because a luminous quality in the place makes it attractive, makes it seem like something that elevates you as you walk through it. The right-hand one has less to commend it. Though filled with people, it has more glare, is less friendly, is more dead in feeling, has less life in it.

OLD FENCE, NEW FENCE

Here the more broken-down example has more life, not less. The older fence definitely seems to have more life. It is weathered, leaning over, adapted to wind, land, water. We get a glimpse here of the fact that life is dependent in some way on time; and that subtle differentiation, adaptation, is a part of what we feel as life.

TWO DOWNTOWN STREETS

Two congested streets, both in downtown areas of cities, Tucson and Annapolis. Still, one of them (Annapolis) has detectably more life than the other. The degree of life is always there, whether the thing is good or bad.

TWO PARTS OF SHANGHAI

Of these two massively built downtown areas, neither are heaven on earth. But still the left-hand one has some vibrancy, some likelihood of human stories, some intense life lived amid the hardness that one sees in the picture. In the right-hand picture, the hardness runs deeper, it is more anal and sterile and repetitive: and one guesses at, and feels, less life in that place.

2 / THE UNIVERSAL FEELING ON WHICH THESE FACTS ARE BASED

What exactly is the nature of the facts which I am bringing forward with all these examples? The essential fact is that in these cases, at least for many of us, the left-hand example of each pair feels more alive than the right-hand example. It is too early yet to describe what lies behind this feeling, or to try to explain it. But I urge you to recognize that the subtle distinction — if you also experience it, as I hope you do — is empirically real, even for cases where not much distinction seems to exist. Even though in a few cases you may have made a different judgment from

the one I have made, still I think you will have found that, broadly, you and I agree.

In our daily life, we can make similar distinctions, comparing places, objects, social situations, even human actions and ecological systems — two leaves, two bends in a river, and so on. We can make these distinctions even in cases that are only slightly different. And, of course, the quality being distinguished, this mysterious life, can appear in very great degree also. The pictures in chapter 1 show more extreme examples in which the life appears to a very great degree.

In historic times, and in many so-called primitive cultures, it was commonplace for people to understand that different places in the world had different degrees of life or spirit. For example, in tribal African societies and among California Indians or Australian aborigines, it was common to recognize a distinction between one tree and another, one rock and another, recognizing that even though all rocks have their life, still, this rock has more life, or more spirit; or this place has a special significance. The Yurok Indians of California, befriended by T. T. Waterman, made innumerable distinctions of this kind, which he recorded: it was common for example for a particular rock to be known as 'fishing rock', or a certain tree to be known as the tree for such and such a purpose.¹

We too—even with our scientific heritage—feel one place to be more significant than another. We feel that a certain tree, or a certain rock, or a certain cliff edge, or a certain clearing, has great power or spirit—or at least, we acknowledge that we feel awe in that place, or we feel an intensity of life. Furthermore, this experience is shared and common. It is not idiosyncratic. Many people feel the same way about just this bend in the Columbia River, this garden gate, this room, this bridge, this stream, this beach.

3 / OUR DIFFICULTY IN RECOGNIZING THE GENERAL QUALITY OF LIFE IN THINGS

Nevertheless, I suspect that many thoughtful readers will have some difficulty with the nature of these facts. Some readers may, indeed, question whether what I call facts are facts, and whether the phenomenon I have indicated is reliable.

This seems an understandable reaction to my proposal. If something of such significance were true in a sense that we of the modern era could accept, one would expect it to be widely known and agreed upon, and one would expect it to be an acknowledged part of our society. If it were true (and generally recognized) that different parts of the world could be more alive and less alive, this fact would then quite naturally be the backbone of all our ideas about architecture and planning.

But it is clearly not the explicit backbone of our thought today. This would seem to speak against the fact which I am claiming. Indeed you, the reader, may have noticed that your first inclination, in at least some of the examples, was to judge them differently from the way I judged them. Is it not likely, then, that this sense of more life or less life in things is a private, idiosyncratic judgment without firm empirical content?

Certainly, if it were indeed merely a personal value judgment, our current sense of how things are in the world would remain intact. On the other hand, if it really were true — objectively — that different parts of space have more life and less life, this fact would have massive impact on our understanding of the world.

It is, therefore, far easier to assume that this is not true. It is difficult to believe that space itself can be alive, in greater or lesser degree. The idea that one part of space might have relatively more life, and another might have less life — and the idea that this distinction would not be based on the presence of biological organisms but might instead be inherent in the space itself according to its structure — would challenge our beliefs about the world to the very roots.

I believe many people who first encounter this idea, at first experience an instinctive refusal to trust the evidence of their own senses in this matter.² But in my view, to grapple with the idea successfully, we must overcome this knee-jerk refusal. To make that possible, I shall, in the next two sections, describe pairs where the relative degree of life is obvious.

4 / THE BANGKOK SLUM HOUSE AND THE POSTMODERN HOUSE

In 1992 I was lecturing to 110 architecture students at the University of California,³ and put on the screen the Bangkok slum house and the postmodern octagonal tower which are shown again here. I asked the students to choose which of the two, for them, seemed to have more life.

For some people the answer was obvious. For others, it was at first not a comfortable question. Some asked “What do you mean? What is the question supposed to mean? What is your definition of life?” and so on. I made it clear that I was not asking people to make a factual judgment, but just to decide which of the two, according to their own feeling, appeared to have more life. Even so, the question was not quite comfortable for everyone.

To make the question more tolerable, I then asked the students to put themselves in one of the following three categories:

• Those who feel the Bangkok house has more life.
• Those who feel the octagonal house has more life.
• Those for whom the question just doesn’t make sense, or who do not wish to answer it even by basing an answer on their own feeling.

Here are the results:

• Eighty-nine said that the Bangkok slum house has more life.
• Twenty-one chose to say that the question didn’t make sense to them, or that they couldn’t or didn’t want to make a choice.
• No one said that the octagonal tower has more life.

To repeat, out of those 110 people, not a single one of them wanted to say (or was willing to say) that the postmodern building had more life than the Bangkok house. This shows an extraordinarily high level of agreement.

Of course the question — and my choice of these two examples — may be ridiculed. The octagonal house looks uninhabited. Was this experiment simply a vote which says that one is occupied and the other isn’t? If so, that would not mean much.

But, under the surface, it was clear, even to people who raised this kind of skeptical objection, that something was going on here. Several of the architecture students among the twenty-one who said they could not judge the issue later came to me and told me that they had felt that the slum has more life, but did not feel comfort-

able saying so. Why not, if the question was indeed so trivial?

I believe it was not trivial, and did not seem trivial to them. I believe that these students were embarrassed by a conflict between the values they were being taught in architecture school, and a truth they perceived and could not deny. In spite of themselves, they saw some quality of ordinary life, with all the feelings that entails, present in the slum, regardless of its poverty, hunger, and disease. And there is some quality of absence of life visible in the octagonal tower which does not go away even if I say that it will be occupied tomorrow.

Thus, in my view, the sense one has in making this judgment is that it is about something real. And because of this, people tend to agree. Indeed it is about something real.

The power of the effect is remarkable—especially when one remembers that most of the hundred-odd people in the audience were architecture students. Given the cultural milieu and ethos of the late 20th century, many of them had come to school to learn how to build things like the postmodern tower. If a hundred of these

students were asked to say which of these two things had more life, and not one of them could bring himself or herself to say that the obviously more architectural one (the one which is more similar to buildings that have been held up to them as models of architecture in other classes) had more life, it is clear that something remarkable was going on under the surface.

Indeed, I think there is no doubt that the students—many of them anyway—found the question disturbing, almost as if a secret, a hidden truth, were being dragged from them in spite of themselves. After having said that the Bangkok house has more life, could that same student then honestly say to himself: "Anyway, the octagonal tower is better," or even, "Postmodern architecture is good"?

Simple though it is, the question has the power to bring perverted values into doubt. The students may have felt it was irritating, silly, an unreasonable question. A few abstained, apparently because they did not like the question, or felt it could not properly be answered. But nevertheless the fact is that the vast majority did, when asked the question, make this judgment, not the other.

5 / THE ILLUMINATED MANUSCRIPT AND THE AUDITORIUM DETAIL

On another occasion, I did a similar experiment, asking students to compare a picture of an illuminated manuscript (as shown in color in chapter 1) with a section of the wall of the auditorium where the lecture was taking place—a wall that was decorated in postmodern fashion with round brass lights and brass strips.

Once again there was strong agreement that, of the two, the illuminated manuscript had more life. But as before, for some students their agreement was reluctant; they expressed themselves irritated by the question, and felt that it was false or "rigged."

The discomfort was voiced by one architecture student who complained that the comparison was "unfair." I asked what it meant to say that it was unfair. The answer came back that in some sneaky sense it seemed to be showing modern architecture in a bad light. Another student complained that the illuminated manuscript was "old." I asked what that had to do with the empirical question: which of the two has more life according to your intuitive, immediate feeling? The answer came back, again, that since it was old it was irrelevant, and it was not a "fair" comparison. But the point of the demonstration was simply to show that people do, indeed, react to things according to the degree of life they have, and that they often agree about it. The very objections that were raised, showed that for the

complainers, too, this was undeniable. And as such, by introducing the idea that such judgments might be objective, the demonstrations cut, once again, to the root of the arbitrariness they were being taught in school, and made the students nervous.

The irritation which students expressed sheds important light on the nature of the phenomenon. It was clear, in the context in which I was asking these questions, that I intended to use the criterion of life as a basis for making distinctions about good and bad in architecture, and that I was intending, further, to encourage students to make buildings which have as much life as possible. Although, on the face of it, it would seem innocent enough and unobjectionable, to ask which one has more life, I believe that it goes to the core of present ills in architectural education and architectural practice.

Is the foundation of modern architecture threatened by this innocent question?

Students found themselves having to stall in order to overcome this awkward intellectual dilemma. They wanted, perhaps, to give the impression that this criterion was hard to apply. And yet to their surprise they found that it was in fact rather easy to apply. Furthermore, the objects which this criterion singled out were not the

models of architecture currently in fashion, but, on the contrary, other things.

It would almost appear, then, that the present fashion in architecture is so hollow that its adherents need to prop it up by refusing to see the life in things, or by refusing to apply this criterion to decide what is good, bad, better. The more one looks at it, the more it seems that the very existence of the criterion threatens the existing intellectual order in the field of architecture.

In short, I believe that architects and architecture students sometimes become uncomfortable when facing this question, because the moment it is asked, they already sense that most people will answer it the same way, and this will be a way which does not speak well for current standards in architecture.

The fact that the life which is being measured has no clear meaning within contemporary biological thought can also cause serious difficulties. Since there is no academic framework on which to pin the question, it can raise doubts of an intellectual nature. Some people have made it clear to me that they are uncomfortable because they cannot make sense of the question, cannot express it in acceptable scientific terms, cannot define for themselves what the

question might really be about. It almost seems to open the door to something forbidden.

The revealing and vital character of this "life" we see and feel in things will become more clear if I draw attention to its "dangerous" character. During the last thirty years I have come to believe that it is difficult to see and accept the existence of life in things, because the social implications of its existence are so extensive. Put simply, if this life in things really exists as I am claiming, that fact alone has enormous ramifications; it implies that many things in our society and way of life may have to change. Fear or a natural reluctance to consider these changes makes us intellectually timid, and less open to the fact itself. Thus one may be unwilling to recognize the existence of this "life" in things, because of a dim—and sometimes perhaps not-so-dim—awareness that if it does exist, then everything in society, and in our view of the world, must change.⁴

For this reason, in a dialogue with a person who is experiencing this kind of trouble, I try to relax him by saying, "I know the question may seem like nonsense, please just go along with me, forget whether the question means anything sensible or not, just give the first answer that comes into your head. To you, which of these two feels more alive?" Once relaxed like this, the person is often more forthcoming, and more willing to express what he feels.

But even then, the nagging voice comes back: "What does this mean? Is it a game?

Where is it leading?" And this nagging voice is made louder by the fact that, no matter what they say, we suspect that most people will give the same answer. All the defenses, which are created in our minds to protect the legitimacy of the mechanistic world-picture, start to argue against the question, do not like it being asked, want to characterize it as nonsense.

There is another reason for the irritation which people may feel. The architecture of the 20th century established certain accepted stylistic norms. The negative examples in both the comparisons I have given are typical of these norms. Yet they are clearly the ones where one feels less life. Immediately, this question therefore opens the door to a serious criticism of the architecture of the 20th century. If typical examples of good design by 20th-century standards have less life than a slum in Bangkok, and less life than an illuminated manuscript from the Middle Ages, any architect who wishes to defend modern and postmodern architecture will almost have to say, "This question doesn't make sense," just to defend his profession and his own self-worth as a professional.

Of course, the question "Which one makes you feel that it is more alive?" is at root simply empirical. But that is exactly why it is so disturbing. Whatever the question means, it seems to probe an area of thought which may have devastating results for the image-based style of architecture current toward the end of the 20th century.

6 / AN ENORMOUS FACT

The examples I have given make it rather clear that, when we go by feeling, there is something at work. We do notice differences in degrees of life in different places, even in the smallest aspects of our daily existence. To a large extent we agree about which cases have more life and less life. And in many cases we feel instinctively that

this greater or lesser life is inherent in the thing.

There is no obvious explanation to hand. The biological-mechanical definition of life does not explain these distinctions. Indeed, not one of the kinds of explanations I have given in my informal comments has the power to explain all the cases.

But there is a growing suspicion — perhaps shared by the reader — that there may be some structure common to all the examples. So many of the reasons for more life in one thing than another refer to structural features: the light, the level of detail, the roundness and completeness, the subtlety, and so forth. Nevertheless, all one can really say with any degree of certainty at this stage is that the judgment about life appears to be a fundamental, primitive quality in things, a fundamental judgment about the world, which appears in every aspect of reality that we encounter.

It is strange that a phenomenon of such power and of such generality — if true — should be missing from our general way of understanding the world. The simplicity of this idea should not make us miss its truly enormous stature. We seem to have a fundamental observation — so far unexplained — that among pairs of events, bits of space, places, and particles of existence, we can usually judge that one has a greater degree of life and the other less, at least according to our feeling. And we have the observation that our experience of this life in things is roughly consistent from person to person.

It is hard to see how society could form a proper conception of its own existence without being cognizant of this fact. Yet, for the last hundred years, modern society has existed almost without this knowledge — and has even built institutions, organizations, and procedures on the basis of conceptions which are absolutely at odds with it.

The possibility that the degree of life of different things and places and events is objective — not solely in the individual — implies that this “felt” life has some part in the scheme of things that is truly enormous. If so, the existence of this felt life — existing as it must to some degree in every single thing there is — would be a discovery, an awakening, at an extraordinary level, perhaps comparable to the 16th-century discovery of the fact that the earth moves round the sun, or the 19th-century discovery of the electromagnetic nature of light.

7 / MY FUNDAMENTAL HYPOTHESIS

Over the years, the observations of this chapter — and others like them which my colleagues and I have made repeatedly during the last twenty years — have led me to believe that the difference in degree of life that we discern in things is not a subjective assessment, but an objective one.⁵ It describes something about the world, which exists in the world, and resides in structure.

I state this by means of the following hypothesis: What we call “life” is a general condition which exists, to some degree or other, in every part of space: brick, stone, grass, river, painting, building, daffodil, human being, forest, city. And further: The key to this idea is that every part of space — every connected region of space, small or large — has some degree of life, and that this degree of life is well defined, objectively existing, and measurable.

The hypothesis means that every part of a building — every windowsill, every step, each speck of dust, the space between this chair and that wall, the roof, the space under the eave, this concrete path, that parking space, the line between the parking spaces — each one has its degree of life. The hypothesis is simple. But it is certainly not something we can consider established. As we shall see in later parts of the book, even the scientific techniques for deciding, empirically, whether indeed this is true or not true are subtle and refined.⁶ I cannot therefore expect the reader to assume that this hypothesis is true. I simply ask that the reader consider that it might be true. I shall then try to present an accumulation of evidence and experience which will persuade the reader that indeed it is true.

The hypothesis appears novel, perhaps because it is so much at odds with the currently popular mechanistic conception of the world which we accept almost without thinking. But I shall try to show that my hypothesis is not a romantic bit of wishful thinking, but that it is an idea which can be formulated precisely in structural terms that can take their place as a normal part of the scientific world-picture.

NOTES

1. Waterman was an anthropologist who worked in the Department of Anthropology at the University of California, Berkeley, during the early decades of the 20th century. The directness and earthiness of his descriptions always impressed me. T. T. Waterman, YUBOK GEOGRAPHY (Berkeley, California: University of California Publications in American Archaeology and Ethnology, 1920, 16 no. 5, 177-314).

2. I believe the reluctance which we may feel in accepting that life and degree of life really are general phenomena, is inevitable — because it comes about as a result of that mechanistic world-view which I have discussed in the preface.

3. Department of Architecture, Fall 1992.

4. For example, in 1991, during public discussion of high-density apartment buildings in Japan, I proposed a form of housing single families in 2 1/2-story cottages, with small lanes, and in which every family has a garden. Rather surprisingly, this kind of housing can be built at 80 families to the acre (200 per hectare) — the same density as typical present-day Japanese high-rise apartment buildings which are 10 to 14 stories high. The cost is the same, too. Which one, therefore, should one build?

In order to help the city of Nagoya, my colleagues in Japan made a survey in which 100 family members were asked to describe their feelings about the kind of housing I had proposed, compared with the 14-story apartment buildings that are usually built at the same cost and density. They were asked which one they preferred, and also which of the two environments seemed, to them, to have more life. Once this survey was made it showed overwhelmingly that the families questioned preferred the low-rise housing. The survey also showed that the families considered this to be a matter of degree of life and that the low-rise housing, in their view, had more life (Hisae Hosoi, OPINIONS OF ONE HUNDRED FAMILIES ABOUT LOW-RISE AND HIGH-RISE APARTMENTS, unpublished ms., Tokyo, 1991).

However, it was surprisingly hard even to get permission to make this survey in the first place. Public agencies in Nagoya went to some trouble to prevent this survey from being made at all by interfering with practical details of the survey process, and by trying to change the questions. I believe this interference happened because, intuitively, the officials working in the agencies guessed what result the survey would have (after all, they themselves would probably have given the very same answers everyone else gave), and yet knew that these answers were at odds with existing policy. They feared this result, and therefore did not want a public survey asking these questions at all. (Details of their attempt to prevent this survey from taking place are given in Christopher Alexander and Hisae Hosoi, THE PRECIOUS JEWEL, forthcoming.) The reason is not hard to find. The form of high-density low-rise housing which I proposed in Japan would — if accepted — upset many present-day forms of land speculation, especially those now seeking to go to still higher levels of density, which would be hampered by natural limits inherent in the low-rise plan. Money interests in Japan therefore supported those who sought to avoid public exposition of these facts.

The very existence of a fact that one kind of housing has more life than the other — if this is indeed a fact — can be potentially unsettling. For a housing ministry, for city departments, developers, banks, and other related interests, even established architectural and construction practices, exploration or even open discussion and acknowledgment of such a fact about degree of life in housing projects, can bring into question a wide variety of firmly held assumptions about architecture and economics.

It is therefore natural that those associated with entrenched interests will assert that the greater life of the one design compared with the other is just a matter of opinion. All this makes the fact itself more difficult to see, more difficult to acknowledge, more difficult to recognize as intellectually and empirically sound.

5. Extensive studies demonstrating the empirical validity and replicability of these judgments have been made by my colleague Professor Hansjoachim Neis, who has undertaken experiments of this kind repeatedly during the last fifteen years. Other studies which confirm the existence of such judgments as repeatable and objective include: Cristina Piza de Toledo, "Empirical Studies Judging the Degree of Life in Photos of Buildings and of Artifacts," masters thesis, University of California, Berkeley, Architecture Department, 1974; Hansjoachim Neis, "City Building: Models for the Formation of Larger Urban Wholes," Ph.D. diss., University of California, Berkeley, Architecture Department, 1989.

6. See chapter 9.

CHAPTER THREE: WHOLENESS AND THE THEORY OF CENTERS

1 / INTRODUCTION

I believe we can understand how “life” is made in buildings, and I offer in what follows a language within which we can begin to describe the phenomenon.

In order to understand life as a phenomenon, it is necessary to define something which I call “the wholeness” and also certain crucial entities which I call “centers,” the building blocks of wholeness. These concepts—and therefore the chapter too—are rather abstract. However, I must ask the reader to try to grasp

and use these concepts, because the wholeness as I define it, and the centers I shall define as the building blocks of wholeness are, in my view, the indispensable tools needed to understand life. With these definitions, we shall be able to see the way that life comes about (chapter 4), the structural features which all life has (chapter 5), the nature of function and ornament (chapter 12). Allow these pages to prepare the groundwork for our ability to understand life as a structure.

2 / THE IDEA OF WHOLENESS

Intuitively we may guess that the beauty of a building, its life, and its capacity to support life all come from the fact that it is working as a whole. A view of the building as a whole means that we see it as part of an extended and undivided continuum. It is not an isolated fragment in itself, but part of the world which includes the gardens, walls, trees, streets beyond its boundaries, and other buildings beyond those. And it contains many wholes within it—also unbounded and continuous in their connections. Above all, the whole is unbroken and undivided.

This rather obvious idea, though we may assume it to be true, does not yet have a precise counterpart in our professional or scientific analysis of buildings. As a general idea, wholeness has been widely discussed by many writers in the 20th century: it is one of the main themes of contemporary thought.¹ In physics, the local behavior of an electron is affected by the larger configuration of the experiment in which it moves.² The local behavior of a gravitational particle is affected by the large-scale gravitational field that is created by the particles.³ In biology, Hans Spemann’s experiments have

shown how the growing cells in an embryo are affected by their position in the whole.⁴ In neurophysiology, Karl Lashley’s experiments on the engram led to his discoveries that any particular memory is encoded not at some locus, but somehow throughout the whole.⁵ In medicine, J. S. Haldane’s discussion of the lung and his explanation of the impossibility of drawing any definite boundary around the organism showed that there is an inseparable quality in which organism and environment are bound together and exist as one whole.⁶ In cosmology, there is Ernst Mach’s principle: the idea that the gravitational constant, $G$ (and hence the force of gravity), is somehow a function of all the matter existing in the universe.⁷ Recent work on the overall ecology of Earth has even shown benefits in regarding the whole planet as a single organism.⁸

In all these examples, the wholeness is the important thing: the local parts exist chiefly in relation to the whole, and their behavior and character and structure are determined by the larger whole in which they exist and which they create.

Although wholeness has, in this intuitive sense, played such a role in contemporary thought, no one has shown how to represent wholeness. We can talk about wholeness, we can be aware of the necessity of seeing things in their wholeness—but no one has yet formulated a way of understanding just what this wholeness is, in precise terms. We have not been able to represent the whole, or even to isolate, in precise mathematical language, what we mean by the whole.

Most artists and architects know, intuitively, that buildings also work primarily as wholes, and that the built world must therefore also be seen in its wholeness. But again—as in the other cases from the recent history of science—we do not yet have the intellectual tools which show us how to do it. We do not yet have a precise

model of a structure we might call “the wholeness” of the built world, or any clear picture of the way this “wholeness” might then contribute to the behavior of the buildings and spaces, what happens there, how it affects us. Nor do we know why it would make sense to say that it is only accurate to see a building working “as a whole.”

After many years of thinking, I believe that I have been able to define, in precise language, what we mean by the wholeness of a given situation. The fundamental idea is that we can define wholeness exactly as a structure. This structure is defined in mathematical language in appendix 1. It is a rather complex structure, analogous in some ways to the underlying structures defined in topology. In the following sections I shall try to explain this idea in informal language, by means of examples.

3 / AN EXAMPLE OF THE WHOLENESS IN A SIMPLE CASE

The general idea is that the wholeness in any part of space is the structure defined by all the various coherent entities that exist in that part of space, and the way these entities are nested in and overlap each other.

To come to grips with this idea, I start by considering a very simple structure, and examining it from the point of view of its wholeness. On the right is a sketch of a blank sheet of paper. Then I place one dot on it. Although the dot is tiny, its impact on the sheet of paper is very great. The blank sheet of paper is one whole, one kind of wholeness. With the introduction of the tiny dot, the wholeness changes dramatically. Its gestalt changes. We begin to experience a subtle and pervasive shift in the whole. The space changes throughout the sheet of paper (and not only where the dot is), vectors are created, differentiations reaching far beyond the dot itself occur within the space. As a whole, an entirely new configuration has come into being, and this configuration extends across the sheet of paper as a whole.

Any reasonable description of wholeness must capture this subtle and pervasive effect. But how is it to work?

What is the configuration which exists after I place the dot? It may be described like this: around the dot, there is a kind of halo. Where the dot has been placed, a larger entity of some kind is created. Also, on each side of the dot, passing the dot tangentially, rectangles of white paper become visible, as further ‘latent’ entities (see diagram on next page). There are four of

these rectangles, and where they cross four other rectangles are formed in the four corners of the sheet (again, see diagram). These corner rectangles are formed by the overlap of the other rectangles, but are also induced by the presence of the dots. In addition, there are rays visible: four white rays going out from the dot parallel to the sides and forming a cross; and four other rays going from the dot towards the four corners. These four rays are not all equally strong. Their relative strength depends on where the dot is on the paper.

Therefore, including the main entity of the sheet itself, there are at least twenty entities created in the space of the paper by the dot. Just what these entities are, is not yet clear, but they are zones, visible as wholes in some fashion. All we can really say is that when we place the dot, these zones become marked in some way, they become visible, they stand out. In some fashion they become coherent, or differentiated, where before they were not. Although the precise nature of these entities is not yet clear, the thing that matters is that they have become more visible, marked, stronger.

In order to visualize the configuration, it is helpful to visualize its structure diagrammatically. We simply list those segments of space which are at the top of the list of relative strength as entities: 1. The sheet itself. 2. The dot. 3. The halo around the dot. 4. Bottom rectangle trapped by dot. 5. Left-hand rectangle trapped by dot.

6. Right-hand rectangle trapped by dot. 7. Top rectangle trapped by dot. 8. Top left corner. 9. Top right corner. 10. Bottom left corner. 11. Bottom right corner. 12. The ray going up from dot. 13. Ray going down from dot. 14. Ray going left from dot. 15. Ray going right from dot. 16. The white cross formed by these four rays. 17. Diagonal ray from dot to nearest corner. 18. Diagonal ray from dot to next corner. 19. Ray from dot to third corner. 20. Ray from dot to furthest corner.

The basic idea of the wholeness, as I define it, is that these stronger zones or entities, together, define the structure which we recognize as the wholeness of the sheet of paper with the dot. I refer to this structure as the wholeness, or $W$. The formal, mathematical definition of wholeness, expressing it as a system of overlapping entities, is given in appendices 1 to 3.$^9$

4 / THE ORIGIN OF THE STRENGTH IN ENTITIES

What is the origin of the “strength” that makes a few special segments stand out as coherent entities to create wholeness? Their strength and centeredness come from a combination of factors that all depend on the overall configuration of the space.

In the example of the sheet with a single dot, we have some centers at the corners — these are zones of space which are highly differentiated. The large rectangles which “fill” the page on the four sides of the dot are the largest symmetrical chunks of space which exist without running into an edge; they are the largest symmetries left intact by the presence of the dot. It is their homogeneity which marks them. The dot itself is marked, of course, because it has a physical differentiation of color. The lines forming rays from the dot to the corner are created again by local symmetries focused on the two points that form the ends of each ray.

We can begin to give general rules which will identify the zones of space that stand out as centers in any given configuration. For example:

• The sets which appear as entities are often locally symmetrical — but not always.
• The entities are usually bounded: that is, at their edge, there is often a sharp change of structure.
• Some of the entities are marked by an internal center where there is another change of continuity near the middle of the center itself.
• There is a simplicity and regularity about these sets which marks them as wholes, and makes them function as entities.
• They are often relatively homogeneous across their interior, compared with the surrounding space.
• There is a topological connectivity in them which marks them as compact.
• They are usually — not always — convex.

This list of characteristics is incomplete, but it begins to suggest the kinds of features which cause the coherence of a segment of space to occur.¹⁰ Later (chapters 4 and 5) we shall see that more complex entities are formed in far more complex ways.

The entities which come into existence in a configuration are not merely cognitive. They have a real mathematical existence, and are actually occurring features of the space itself. They may be established mathematically according to the relative hierarchies of differentiation in the space. They are mathematically and physically real.

And they have different degrees of strength.

5 / THE CONCEPT OF A CENTER

Let us now consider the nature of the entities from which wholeness is built. We may consider any configuration in the world, a building, a street, a room full of people playing cards, a crowd of people, a forest. Each has its wholeness. By that I mean that there are visible within that thing, a huge number of entities, at different scales, formed very much in the ways I have described, and that the totality of these entities with the way they are nested constitute the wholeness of that thing.¹¹ We may think of these entities as parts (as they may sometimes seem to us) or as local wholes or sub-wholes. But, as I have illustrated in the case of the sheet of paper

and the dot, these parts and entities are rarely pre-existing. They are more often themselves created by the wholeness. This apparent paradox (seeming paradoxical only because of the simple-minded way in which it is expressed) is a fundamental issue in the nature of wholeness: the wholeness is made of parts; the parts are created by the wholeness. To understand wholeness we must have a conception in which “parts” and wholes work in this holistic way.

To have a consistent way of talking about these entities, during recent years, I have learned to call them all (whether parts or or local wholes or hardly visible coherent entities), “centers.”¹² What this means is that each one of these entities has, as its defining mark, the fact that it appears to exist as a local center within a larger whole. It is a phenomenon of centeredness in space. Thus a human head, or ear, or finger is a discernible whole. It is also, both visually and functionally, a center. We experience it as a center. And it is, in the end, its centeredness which is its most clear, defining mark.

In using the word center in this way, I am not referring at all to a point center like a center of gravity. I use the word center to identify an organized zone of space — that is to say, a distinct set of points in space, which, because of its organization, because of its internal coherence, and because of its relation to its context, exhibits centeredness, forms a local zone of relative centeredness with respect to the other parts of space. When I use the word center, I am always referring to a physical set, a distinct physical system, which occupies a certain volume in space, and has a special marked coherence. Even when the center is a social or cultural center, it is still ultimately spatial as well: it occurs in space, and always has a spatial locus.¹³

There is a mathematical reason for thinking of the coherent entities in the world as centers, not as wholes. If I want to be accurate about a whole, it is natural for me to ask where that whole starts and stops. Suppose, for example, I am talking about a fishpond, and want to call it a whole. To be accurate about it in a mathematical

theory, I want be able to draw a precise boundary around this whole, and say for each point in space whether it is part of this set of points or not. But this is very hard to do. Obviously the water is part of the fishpond. What about the concrete it is made of, or the clay under the ground? Is this part of the whole we call “the pond”? How deep does it go? Do I include the air which is just above the pond? Is that part of the pond? What about the pipes bringing in the water? These are uncomfortable questions, and they are not trivial. There is no natural way to draw a boundary around the pond which gets just the right things, and leaves out just the right things. In a very rigid way of thinking, this would make it seem that the pond does not really exist as a whole. Obviously this is the wrong conclusion. The pond does exist. Our trouble is that we don’t know how to define it exactly. But the trouble comes from referring to it as a “whole.” That kind of terminology seems to make it necessary for me to draw an exact boundary, including just those things which are part of the pond, and leaving out just those which aren’t. That is the mistake.¹⁴

When I call the pond a center, the situation changes. I can then recognize the fact that the pond does have existence as a local center of activity: a living system. It is a focused entity. But the fuzziness of its edges becomes less problematic. The reason is that the pond, as an entity, is focused towards its center. It creates a field of centeredness. But, obviously, this effect falls off. The peripheral things play their role in the pond. But I do not need to make a definite commitment about the edge, and what is in and what is out, because that is not the point. What matters in the existence of the pond as a coherent entity is that the organization of the pond is caused by a field effect in which the various elements work together to produce this phenomenon of a center. This is true physically in the actual physical system of the pond: water, edge, shallows, gradients, lilies — all help in the formation of the pond as a center. And it is also true mentally in my perception of that pond. That is why it is more

useful, and more accurate, to call the pond a center rather than calling it a whole. The same is true for window, door, wall, or arch. None of them can be exactly bounded. They are all entities which have a fuzzy edge, and whose existence lies mainly in the fact that they exist as centers in the portion of the world which they inhabit.

There is yet another reason for preferring the term "center" to the term "whole." The entities we are concerned with in a building include the most ordinary elements like staircase, bathtub, door, kitchen sink, room, ceiling, door, doorway, window, curtain, and kitchen nook. Ultimately, in dealing with design, we have to ask, What is the proper relationship among these elements? Here again there is a powerful reason for using the term "center." From the point of view of relationships which appear in the design, it is more useful to call the kitchen sink a "center" than a "whole." If I call it a whole, it then exists in my mind as an isolated object. But if I call it a center, it already tells me something extra; it creates a sense, in my mind, of the way the sink is going to work in the kitchen. It makes me aware of the larger pattern of things, and the way this particular element — the kitchen sink — fits into that pattern, plays its role in that pattern. It makes the sink feel more like a thing which radiates out, extends beyond its own boundaries, and takes its part in the kitchen as a whole.

On the other hand, if I call the sink a whole I have more of a feeling of boundedness. I lose the relationships which exist among things. It is as if I have drawn a skin around the sink, made it entire within itself, but cut it off more from what surrounds it. I am therefore less aware of the relationships it has, or will have, or should have, with the larger kitchen, and think of it more in itself, enclosed and shut off.

On one occasion, I was discussing the concept of centers, as it applied to some bedroom curtains, with my wife Pamela. She made the comment that the use of the word "centers," as I had explained it to her, was already changing her view of everything around her, even as we were talking: "When I look at the curtain in the room, and think of the curtain, the curtain rod, the window, the sky, the light on the ceiling, as centers, then I become so much more cognizant of the relatedness of all things — it is as though my awareness increases, almost like eating the fruit in the garden of Eden; my eyes suddenly perceive everything in such a different way; I see the world in all its relatedness, and as it really is."

The same is true of all the entities which appear in the world. When I think of them as wholes, or entities, I focus on their boundedness, their separation. When I think of them as centers, I become more aware of their relatedness; I see them as focal points in a larger unbroken whole and I see the world as whole.

6 / WHOLENESS AS A SUBTLE STRUCTURE

In order to understand the way that centers are induced by the surrounding wholeness, let us refer once again to abstract examples. It is essential to note that the centers always become centers as a result of the configuration as a whole. For example, if I make a square like the one in the drawing on the next page, then this square appears as a strong center. If I add two black triangles to the configuration, then even though the

square is still there, the square is no longer very strong as a center, while other triangles have become relatively more strong and overshadow the original center, which has now "disappeared."

Thus the strength of any given center is not merely a function of the internal shape which creates that center in itself, but comes about as a result of the influence of many other factors which extend outward in the given region of

In the first sketch, the square appears as a strong center. In the second sketch, after addition of the dark triangles, even though the square is still there, it no longer has the same strength as a center, because of the changed condition in the configuration as a whole.

space, always as a result of the configuration as a whole. This follows, anyway, from the list of mathematical features which are responsible for causing the strength. Symmetry, connectedness, convexity, homogeneity, boundaries, sharp change of features, and so forth are all functions of the configuration as a whole. The centers which make up any given wholeness do not exist independently, but appear as elements which are generated by the configuration as a whole. It is the large-scale features of the configuration which produce the local centers and allow the local centers to 'settle out.'

The wholeness in any given part of space is highly fluid, and easily affected by very small changes of geometry. Indeed wholeness changes continuously through time, and is dependent on subtle—sometimes even minute—changes in the configurations in it and around it. This happens because the centers which occur are induced in a very subtle fashion, and therefore change quite markedly as even small changes are made in the fine structure of the configuration.

Consider again the sheet of paper and the dot. We have seen how one dot on the blank sheet of paper induces a widespread global structure in the wholeness of the sheet of paper. One little dot, whose area is no more than 0.0001 of the sheet, thoroughly changes the wholeness of the sheet.

Now look (Case 1, next page) at what happens when another dot is added. Entirely different centers are strengthened, and the structure suddenly becomes like a head. Or look (Case 2) what happens when the second dot is added in a different position. Again quite new centers are

created and, as a result, the structure suddenly becomes diagonal-like, with induced triangles and an upward-thrusting diagonal line like an arrow.

Like the first dot, each of these second dots is not more than 0.0001 of the sheet. Yet again this tiny change (tiny in actual area or volume) utterly alters the wholeness of what is there. So in each case the structure, which I call "the wholeness," of a thing is extremely susceptible to relatively minor changes in its details. The wholeness changes globally—and sometimes completely—as a result of very small local physical changes.

Thus it is clear that the wholeness is a structure of great subtlety which is induced in the whole. It cannot easily be predicted from the parts, and it is useless to think of it as a relationship "among the parts." The wholeness is an autonomous and global structure, which is induced by the details of the configuration. It is a real physical and mathematical structure in space—but it is created indirectly, by symmetries and other relationships which are induced in the geometry. To grasp the nature of this subtle structure fully, we must learn to avoid the danger of trying to see centers made up of parts. Present-day conventional wisdom (perhaps Cartesian and mechanistic in origin) tells us that everything is made of parts. In particular, people believe today that every whole is made of parts. The key aspect of this belief is the idea that the parts come "before" the whole: in short, the parts exist as elements of some kind, which are then brought into relationship with one another, or combined, and a center is "created" out of these parts and their combinations as a result.

I believe accurate understanding of wholeness is quite different. When we understand what wholeness is really like as a structure, we see that in most cases it is the wholeness which creates its parts. The center is not made from parts. Rather, it would be more true to say that most of the parts are created by the wholeness. They settle out from the wholeness, and are created by all of it. This is analogous to the way a

whirlpool is created in a stream. The stream whirls, and the centers we see as the whirling (vortex, stream-lines, etc.) are created by the larger configuration of banks, rocks, and so forth. So, within this whirling, we observe a whirlpool which has formed. This is fundamentally different from the idea that wholes are made up from elements or built from parts.

We may see the phenomenon as I believe it to be in the two-dot examples, where the visible things that look like parts are induced by the whole. Thus the visible diagonal in the second case of two dots is something we might call one of its "parts." But it is not a pre-existing element. It is a part which is induced by the action of the whole. It "breaks out" naturally from the whole. In no sense at all is it an element from which the center is built.

When we understand things in their wholeness, this is the general rule. The sub-wholes — or centers — are induced within the wholeness, and come from the wholeness. And because of this, the parts are adapted and modified, in shape and size, by their position within the whole. The petals of a flower are not identical. They are similar, but each one is slightly different according to its position and history in the whole. When parts repeat we never have identical repetition. Instead we have repeated parts as centers which are changing and variable according to their position in the whole, as they repeat within the whole. In nature, this follows directly from the fact that parts are induced by the whole and created by the whole. The whole is not created out of them. The flower is not made from petals. The petals are made from their role and

position in the flower. This is an entirely different vision of reality from the one we have become used to. In this new vision, it is always the whole, the wholeness as a structure, which comes first.

Everything else follows from this wholeness, and from the centers and sub-centers which are induced within it.

7 / A FURTHER EXAMPLE OF WHOLENESS AS IT IS CAPTURED BY THE SYSTEM OF CENTERS

I hope the wholeness, $W$, as I have defined it, actually is beginning to capture that character we intuitively think of as “the whole.”

Consider these two drawings of arches, A and B. The drawings are superficially somewhat similar, but the feeling they have is very different. We are aware, if we pay attention, that as wholes, they have a pronounced and different gestalt.

“A” has an arch form, a marked center in the middle at the point of the arch, and an overall coherence. “B” is a simpler, rectangular version of the same thing. But the difference is greater than these words suggest. The two really have extremely different character.

If we focus on the space as a whole, we see how different they are. The pointed one, A, has a focus on the point of the arch. It is united. One sees two wedge-shaped swaths of space to the left and to the right, emphasizing the way the sharp point almost cleaves the space above. The point is also very strongly marked. The second arch, B, is much more blunt. The main thing one is aware of is the stillness of the large square of empty space above the arch. The top of the arch, chisel shaped, is also still. One sees the two legs

on either side as appendages. All this is what we mean by the "wholeness" of the two drawings.

DRAWING A. In the drawing labeled "Structure of A," I have outlined the most salient centers which appear within the space of the drawing and form the wholeness $W$. We can see that the centers I have marked form a kind of nested sequence. There is one at the vertex. There is another which is the triangle of space below the vertex that includes the vertex. There is another which is the whole arch. On the right and left of the arch, there are yet other upside-down trapezium-shaped wedges of space. Then there is a kind of rectangle of space next to the arch on each side of the arch.

Together these visible centers form a kind of swooping movement which starts at the top of the drawing, goes down either side, and then comes up the middle, culminating in the point of the arch. They form a nested structure, which emphasizes the point of the arch and supports the entity that is the arch. The wholeness that we experience—the overall gestalt of the whole thing—is precisely captured by the structure $W$.

DRAWING B. In the drawing labeled "Structure of B," I have again outlined the strongest centers which appear to form its wholeness. In this case the centers form a somewhat less coherent structure than in A. There is one center in the rectangle at the top, across the top. There is another down each side. There is one center in the arch. These centers fit together in a fashion that roughly resembles the structure of the centers in drawing A, but it is a different structure. For example in B the rectangle across the top is stronger and far more dominant than it is in A. The centers inside the arch are less nested and less dominant than in A. An overall structure exists in B as it does in A, but appears to be less coherent, less bound together.

In both drawings, the system of centers describes the wholeness we intuitively experience in the thing. And we have a hint of the way the wholeness $W$ also begins to describe, and explain, the difference in life between the two drawings. A has more life than B, even if only slightly, and we find this fact reflected in the more coherent structure of its wholeness.

8 / THE FUNDAMENTAL ENTITIES OF WHICH THE WORLD IS MADE

Let us move on, now, to consider the appearance of the wholeness $W$ in real world examples.

In the foregoing examples we saw how the wholeness of each drawing — the broad sweep of the thing — may be seen as the pattern of the main centers which exist in the space of the drawing. In the arch drawing, the centers are the plain and simple swaths of space and the special bits which stand out, like the apex of the arch or the point where the line of the arch meets the uprights. When we take these centers together, we see how they form themselves into still larger centers — the sweep of the arch, the symmetrical system over the point of the arch, and so on — and that it is then the pattern of all these centers working together which forms the whole.

What exactly, then, is wholeness? That is the crux of the matter. My answer is that the wholeness is not merely a way of focusing on the gestalt of the thing, but is instead a real structure, an actual "thing" in itself. It is a structure which exists in the world that includes what we intuitively perceive as the gestalt, the overview, the broad nature of a thing. It is the source of the coherence which exists in any part of the world.

This wholeness gets its strength from the coherent spatial centers of which it is made. If there are roses around a front door of a cottage, that is what you remember; if there is a pair of ducks in the garden, and a fishpond, it is the ducks and fishpond you remember; if there is a great and wonderful room with mattresses where everybody sleeps — as in an Austrian mountain hut — then that is what you remember. The roses, the ducks, and the mattresses are all centers, and it is these entities or centers which mark something as what it is, which make it memorable, remarkable.

The coherent centers define character, and create arrangement. The main coherent centers which exist in a place determine what it is like there, what kind of life it has. The centers are the most fundamental things we notice in what is happening. They affect us most. And this importance of the coherent centers, as the entities which govern the character of a thing, appears on a more physical level too. If a building has a room with an enormous gilded ceiling, it is that ceiling we remember. If the room has immense windows with hundreds of panes looking toward the soft east light, it is those windows we remember. The Stefansdom in Vienna has a huge eagle on the roof. It is the roof we remember, and the huge eagle on it. If one building has columns which are blank concrete shafts, and another has capitals, with a wonderful shape, painted and round, it is these capitals we remember. If a building has a skating rink outside, like Rockefeller Plaza in New York, it is the skating and the skaters we remember.

These are the explicit, obvious centers. And they are not only spatial. Other centers, some hidden, some hardly visible in the space, but latent, or biological, or social, also control the behavior of the world. The arrangement, shape, and pattern of buildings, rooms, streets, and furniture come from the centers again. That which we commonly call "arrangement" — as in the simple example of the two arches in drawings A and B — is also created by centers. Even shape is dominated by the centers and sub-centers which form it. A cross is created by one center at the crossing point, four centers at the extremities, with their larger centers formed by their overlapping relationships to one another. A circle is created by a continuous system of identical centers forming short arcs around the perimeter, neighboring ones overlapping each other and coming back to join themselves, with larger centers in the void of the circle to form the core.

The wholeness of any portion of the world is this system of larger and smaller centers, in

their connection and overlap. The wholeness of a window includes the coherent space which binds the window together—its sill, glass, the sloping reveals, its mullions, the landscape outside, the light coming in, the soft light on the wall next to the window, the chair drawn up toward the window's light—and the formation of larger centers which makes them one: the space of the window seat which binds the window reveals, seat, sill, and window plane; the view which combines chair, outdoor landscape, and the glazing bars; the light falling on the window reveal and on the floor. Here, as before, the wholeness is defined by the major centers—entities—and the way these centers are arranged to form still larger centers. Some centers are explicit. Like the dot, which we

see easily; others, like the space around the dot, we see with more difficulty, because it is more subtle. In the photograph on this pages, the cottage is given its character partly by the explicit and obvious centers—the roses, the arched trellis on which the roses climb, the surface of the roof, the individual tiles which form that surface. And, partly, it is given its character by the less visible centers, formed and induced within the wholeness—the “hole” of the archway beneath the trellis, the space in front of the cottage wall, the line in space which connects the archway to the small window in the cottage wall. All the centers together, explicit ones and hidden ones together, form the wholeness in this cottage, as they do in any given part of the world at any moment.

9 / THE SUBTLETY OF CENTERS WHICH EXIST IN THE WORLD

Let us now consider a further example of the subtle wholeness as it appears in the real world. Look at the scene in the photograph on the right. We see a tree, a road, and a bicycle parked at the edge of the road under the tree. In our normal way of looking at this scene, we see various fragments which seem to be "parts" of the whole: the tree, the road, the bike, the cyclist.

Learning to see the wholeness as it is in a case like this, not muddled or contaminated by words and concepts, is extremely difficult, but it is possible to learn, consciously, to pay attention to this wholeness. (The difficulty is discussed at some length in appendix 3, where I also give one example of a technique for helping a person see wholeness as it is.[15])

When we see wholeness as it is, we recognize that these seeming parts—the road, the tree, the bike, these particular centers—are merely arbitrary fragments which our minds have been directed to, because we happen to have words for them. If we open our eyes wide, and look at the scene without cognitive prejudice, we see something quite different: a great swath of space, wider than the road, which extends to the distance and includes the flat land on either side of the road as one of the major centers in the scene (center #1 in the diagram). We see a space under the tree, between the road and the tree, as another obvious "place" or center within the scene. We see the spot where the

person is leaning, on the right side of the tree, as a major point of concentration. Also, if we look carefully, we see a flat, ring-shaped swath of space under the tree, almost like a flat cylindrical donut, caused by the fact that the tree's foliage has been trimmed to just above head height all around (center #2 in the diagram). And we see the top of the tree, the wooly, beehive shape of the tree itself—but it is not the tree which draws our attention as an entity—it is the top of the tree without the trunk—the mass of foliage (center #3 in the diagram). Thus the centers we see, when we look for wholeness, are not the centers which are captured by words, like "road," "bike," and "tree," but a different set of centers, which have no special words attached to them, and which are induced structurally by the overall configuration of this scene.

The wholeness of this scene is created by these centers, all of them together. They are really there, actually existing centers in the space. It is not our imagination, and not some conceptual occurrence. Their existence and their strength becomes visible when we make our minds blank and look without focusing at all parts of the page at once. In this unfocused or defocused state, we see the big swath of space over grass and road, we see the cottonwool top of the tree, we see the trunk and the ring of space around it as the strongest things. The things which have easy names—the tree, the bike, the road (though they too have their relative degree of wholeness and centeredness) are less strong within the overall configuration. They are centers, too, but they are lesser centers within this configuration, and play a less important role within the structure as a whole.

For example, why does the rider of the bike put his bike under this tree? What invites him to stop, what invites the bike to be there at all,

is the donut of space under the tree, not the tree itself. Thus the wholeness and its real system of centers, hidden and not-hidden, are the structures which have impact on the world. We shall not understand how the world works unless we pay attention to the structure of wholeness as it is.

Consider, from this enlarged perspective, a rather more complex case: my family's garden in West Sussex, England. What is most noticeable

about the garden is the way it has life. The ducks come up from the pond, following one another, to the gate. The plum tree is on the sheep meadow. The tennis court, at one corner of the garden, is shielded by rows of apple trees, heavily laden with fruit. In the main flower border the roses bloom; the driveway comes up to the house between nettles and hawthorn hedges. The cats bring the rabbits they catch, and leave the innards of the rabbits on the back terrace. The meadow by the stream floods in the winter, and the following spring the meadow is thick with flowers.

What makes this a living structure is its wholeness. And what exactly is its wholeness? It is the white-washed brick house, standing four-square and simple, unadorned in the field. It is the huge kitchen, the largest room, lit on two sides by garden windows, with a big warm stove warming the kitchen constantly as it heats the hot water; the kitchen table, long, with eight rush chairs around it; the hallway, generous, uncluttered, a room in itself that you enter as you come into the house. The centers which make this farmhouse

what it is, and the life which occurs in the farmhouse, are inseparable. It is the centers which create its behavior, its nature, its substance.

Although one may be misled into thinking about design, the features which design seems to deal with are minor, have less importance. The centers — the coherent entities which form the whole — are life-affirming, massive in their effect, and tremendously concrete, so that minor changes in design could not sway them, or upset them, or change them.

For example: the duck pond, surrounded by the pasture on one side, by the chicken run, with the small seat on one side and the island where the ducks go to escape the fox at night. All these are the effective centers, which make the life of the ducks at the farm.

For example: the stone terrace outside the kitchen, leading out onto the lawn, with the cat door in it. It is the place where we sit, go out to cut flowers in the rose beds just beyond. The flagstones which form this center have an enormous role in the active life of the house.

In the wholeness of this garden, we find that, once again, it is the real centers — the most coherent centers as they actually are, not those which happen to have convenient names — which dominate the feeling and behavior of the place.

Consider the wholeness of the building and the lane together. Suppose there is a garden in front. Perhaps there is a porch, a stone platform at the door, flowers in the garden, a hedge along the lane, and at the back of the garden the wall of the house itself, windows in that wall, a roofline — and so on.

What does it mean to see all this from the point of view of wholeness? I notice the sunny part of the garden itself as a space. The place where the roses are climbing near the kitchen catches my eye. The path to the front door, and the steps from the back porch, and the door itself, the door of the house, all work as a unit, as a continuous center about 40 feet long. The sunshine and the roof edge, with the rafters repeating under the eave, together form a pattern of light and shadow which leads my eye, and forms a boundary of the house against the sky. Perhaps there is a reflection from one of the windows. The window and its curtains form a frame for what I see behind in the darkness of the room.

All this is much more like a pulsating unity than the "conceptual" or intellectual image of the house. In our conceptual picture of the house, we have things called street, garden, roof, front door, and so on. But the centers or entities which hit my eye when I take it all in as a whole are slightly different. I see the sunny part of the garden where the sun is falling on the lawn as a center—not the entire "garden." I see the swath of space which unites front steps, front path, and front stoop, not the "front door." I see the roofline and the light and shadow of the eave, not the "roof" as such. Also there is a thing which I might call "garden-plus-street"—a center where the flowerbed meets the street. This is

entirely different from the conceptual and verbal entity "street" or the conceptual and verbal entity "house." It straddles conceptual boundaries.

The difference is deeply functional, not just a matter of visual perception. The centers we see when we look at the thing in its wholeness are the ones which are responsible for its real behavior. For example, it is the sunny part of the garden which makes a difference to the way the garden really works, not the abstract or conceptual entity marked "garden" that is bounded by the house and the fence. It is the swath of space going from the front gate, over gravel, past the roses to the front door which actually controls the way we feel as we approach the house and enter it—not the conceptual entity "front door." It is the bit of land where garden lawn meets fence and field where the sheep graze, backed up by the willow over the lawn, where we often pull our chairs in the shade, that allows us to sit there drinking our tea, watching the world go by—and this affects the life and feeling of the house in its relation to the world much more substantially than any characteristic of the abstract entity we call the "garden."

Thus the centers we notice when we see the situation in its wholeness are not only more dominant to the eye. They control the real behavior of the thing, the life which develops there, the real human events which happen, and the feelings people have about living there. The house-garden complex seen in its wholeness is truer perceptually and more accurate functionally than any analytic vision of the house or lot or garden taken by themselves.

It is apparent, if we think carefully, that we are not used to seeing—or looking at—this kind of structure in the world around us. If we consider a garden and a house from this point of view, the deep centers hidden in the house and the garden are unexpected, just as they are in the sheet of paper with a dot. They are subtle, perhaps invisible to a casual observer. Yet it is these centers and their structure which give the thing its life.

10 / WHOLENESS AS A FUNDAMENTAL STRUCTURE

Everything that follows in this book is a view of physical reality dominated by the existence of wholeness as I have defined it.

I propose a view of physical reality which is dominated by the existence of this one particular structure, W, the wholeness. In any given region of space, some subregions have higher intensity as centers, others have less. Many subregions have weak intensity or none at all. The overall configuration of the nested centers, together with their relative intensities, comprise a single structure. I define this structure as "the" wholeness of that region.¹⁶

This structure exists everywhere in the world. It exists in nature; it exists in buildings; it exists in works of art. It is a fundamental structure in space which not only encompasses the wholeness or gestalt of the thing; it also encompasses the obvious parts, or elements, from which this thing is made.¹⁷

I am firmly convinced that the nature and behavior of buildings and other artifacts can only be understood within the context of this structure. In particular, objective recognition of the fact that some buildings have more life than others, and are objectively more beautiful and satisfying, can only—I think—be achieved in the context of this structure.¹⁸

I believe, too, that life, in an ordinary biological sense, is itself also created from this wholeness: and that efforts to explain it in more mechanical fashion will go on failing, as they have in recent decades.

A crucial feature of the wholeness is that it is neutral: it simply exists. Determination of its details may be made by neutral methods, yet at the same time—as we shall see in later chapters—the relative harmony or "life" of a given building may be understood directly from the internal cohesion of the structure. Thus, the relative life or beauty or goodness of a given part of the world may be understood, I shall argue, without reference to opinion, prejudice or philosophy, merely as a consequence of the wholeness which exists.

11 / THE GLOBAL CHARACTER OF WHOLENESS

I have not yet emphasized the enormous power of the wholeness, W. This structure catches the overall character in a way which is almost mysterious, but goes to the heart of many things not easily explained. This happens because it is an overall field-like structure, a global, overall effect. It is distinct, completely distinct, from the elements or "parts" which appear in that wholeness; it is unusual in our experience, yet catches what we have often thought of as the artistic intuition about the whole.

I know of no example which makes this more clear than a famous one which appears in an essay on portraiture by Matisse.¹⁹ He talks about the fact that the character of a human face is something which is deep in the person, deep in the face, and may not be captured by the local features in the normal sense at all. To make his point, he shows four drawings he made of his own face. These drawings, reproduced below, are remarkable. The features, in the normal sense, are different in each drawing. In one he has a weak chin, in another a very strong chin. In one he has a huge roman nose, in another a small pudgy nose. In one the eyes are far apart, in another they are close together. And yet, in each of the four faces, we see the unmistakable face and character of Henri Matisse. As Matisse says, the

character is something deeper than features: it is an inner thing which exists over and above the features, and is not even dependent on these features.

What in the world is going on? What is it that Matisse is seeing? How is it that we see Matisse's face, in each case, even though the features are so entirely different? What is this elusive "character" in a person's face which Matisse can see so well, and which we fail to see as clearly?

The answer is, this "character" is the wholeness. It is the overall vector, the overall qualitative structure, the overall field effect of the face. It is a global pattern-like aspect of the face which is the same in all four pictures. How should I describe this wholeness? It is the bald head with the eyes and with the eyes spreading concentrating downward, coming to a point somewhere around the mouth. Also the lower part, mustache, jaw, etc., somehow spreads outward again. We do not

Four different self-portraits of Matisse: the features are different in each case; only the wholeness remains the same in every drawing.

have an easy language for describing this kind of overall structure. But it is indeed this overall structure of the centers that is responsible for the wholeness. And, as far as this is concerned, it is the same in all four drawings. And it is the same, too, of course, in the photo of Matisse—because that is actually what was in his face. The wholeness of this face is that thing which is common to all four drawings, and includes none of that which is different in the four drawings. Thus the drawings accurately reflect the wholeness of Matisse's actual face, even though this wholeness is produced in conjunction with local features which vary enormously.

This definition makes it clear how much the wholeness is a global thing—easy to feel, perhaps, but hard to define. You cannot get the portrait of a person right unless you can see this underlying wholeness, this underlying inner character. Drawing the features correctly does not necessarily achieve a resemblance. How many artists, in their first attempts at portraiture, have found this out, in frustration? If you want to draw a person, you have to draw the wholeness. Nothing else will get the likeness.²⁰

In portraiture, as in architecture, it is the wholeness which is the real thing that lies beneath the surface, and determines everything.

12 / WHOLENESS AS A FUNDAMENTAL PART OF PHYSICS

The vital part played by wholeness as the fundamental substratum that governs the behavior of the world extends far beyond architecture and art. Even in modern physics, the "toughest" of the sciences, revolutionary experiments made during the 20th century have indicated that the most mechanical events—for example the path taken by an electron flying through a geometric pattern of slits—are also governed by the wholeness of that field, not only by the classical forces acting on the electron.

One of the most puzzling experiments of the 20th century is the two-slit experiment. In this experiment, electrons pass through a pair of slits, and then land on a wall: the experiment counts the electrons arriving at different positions on the screen. What has been shown conclusively is that the pattern of electrons arriving on the wall cannot be explained by the normal classical picture of mechanical forces acting on the electron.

Physics has concluded that, in some way, the electron is guided by the wholeness of the experimental configuration.²¹ The mathematics is well understood. But the physical interpretation is

not understood, even to this day. Although the analysis and interpretation of the way wholeness should be understood has not yet been agreed upon, there are strong reasons for thinking that the wholeness which causes the motion of the electron is essentially the same wholeness we have already defined: the system of centers created by the spatial configuration of the experiment.²² What is most remarkable is that it appears that this wholeness influences the movement of electrons in a way that exists over and above any mechanical effects caused by electromagnetic fields and conventional nuclear forces. Thus the wholeness has a fundamental part to play in governing the behavior of matter.

Further details of this experiment, and its interpretation in terms of wholeness, are given in appendix 5. But the essential point for the reader is to recognize that the wholeness, defined as the pattern of centers in some part of space, is not only the underlying causative structure in matters of architecture and art—but that even the behavior of subatomic particles, electrons, is also governed by this wholeness. Wholeness is a truly pervasive structure, which acts at all scales.

In appendix 2 and appendix 3, and above all in appendix 6, I give other examples of the power which the wholeness, $W$ , has to explain hitherto unexplained phenomena, because it emphasizes, and makes concrete, the wholeness that is really there.

13 / WHOLENESS AS THE UNDERLYING SUBSTRATE OF ALL LIFE IN SPACE

Seeing the power of the wholeness in matters of psychology, and art, and physics, we get some inkling of its potential. I believe that it holds the key to much of what happens in the world, and certainly the key to what happens in buildings, their effect on us, their life. The real character of the world, its flesh, is governed by the centers in the geometry.

Look at the street illustrated in the picture below. What is the origin of its life at this moment, the basis of its nature? It is the pattern of hydrants on the sidewalk and the centers which they form, the centers formed by the front steps and windows together with the street. These things do not have names, but once again it is the wholeness from which its life originates. It is the

particular system of centers, peculiar to this street, and the life which emanates from them.

Similarly, even the strange mood of these rooms in the Middle East, haunting, perhaps a brothel, perhaps a harem — depends entirely on its centers. The dark-eyed women, veils, heavily patterned wallpaper, rooms, and doorways leading on — this mood is formed by the centers.

In traditional Japan, there is a small garden, a bridge, tatami mats on the floor, a sliding

screen, paper on the sliding screen. These centers are particular to traditional Japan. In India people are comfortable sitting on the ground, even in a public railroad station, because they view their ownership of the ground in another way unfamiliar in the West; to them, all ground is really theirs to use as they wish.

Such centers, each typical for its culture, are carried by culture, and define centers in society and in the built world. Thus one cultural fact of

India exists in the fact that there are some centers made of people sitting and lying on the ground, in railway stations, others carry the same feeling even into a forest as in the scene above. These are peculiarities of India. The two Indian scenes il-

lustrated are formed by such centers: on the next page, people sitting and lying in a public place during a storytelling episode; above, in the forest, the loose aggregation of space, the trees spaced apart, the flowing saris and the space

which they create. This is one of the myriad things which give India its special substance and character.

In human society, the wholeness of a given part of space always includes the cultural milieu. In India, the wholeness includes the pervasive existence of centers in which people sit, squat, sleep on the ground. In America this would be an aberration, for which a person might be arrested.

All this depends on the wholeness, $W$ , and its particular state in various parts of the world. $W$ — that is, the particular system of centers — governs and defines the cultural variation which we experience in the world.

In a large building, consider the organization: approach, gardens, entrance, main rooms, main structure, doors, windows, ceilings, stairs, the character of the movement from room to room, the character of space in any given room—all this is given by centers. And the life that happens there—the social life, the gather-

ings, meetings, the private conversations, individual workplaces, the place to sit, the meals, the welcoming, and leave-taking—all this too, is embodied in the centers of the building.

Look at the interior of the Hagia Sophia, on the previous page. One system of coherent entities we observe are the light rays. These centers are changing—as the sun moves, so the light rays move. The centers which appear and disappear are evanescent, impermanent, in flux. Further, the homogeneity which forms these centers is subtle. Here the material, which is air, is continuous throughout the space. But some dust particles floating in the air catch the light, so it is these lit dust particles that form the ray and, of course, the actual waves of light, which pass through the air and illuminate the space. This example broadens our idea of architecture, because we recognize that these kinds of transitory event-like centers play as huge a role in the way a building is and works as the more obviously fixed elements like columns and floors.

Consider another case. Two boys, whispering, talking about their secrets, in a shed. Here

again we have a situation which is of the essence of architecture. It is this moment, long remembered—unconsciously if not explicitly—which makes the magic of those years, and it is this shed, able to nurture those private conversations, which is a living part of the world. In this case, what are the centers? They are even more evanescent than the sunbeams. It is the human situation, the two boys together: it may last five minutes, then fall apart. It is a human association, a living moment, which existed at that moment when the photograph was taken, and is now gone forever. It may have recurred, in slightly different form, hundreds of times. But again, the centers which form when these boys talk together, which is this association between the boys, is essential to a proper understanding of architecture: here we have a case which is almost purely human.

Finally we may consider even less architectural cases: the pregnant woman, with the baby in her belly; the young man kissing the hand of the priest; the players of some string quartet, playing, sitting together, looking at their music on the music stands, making the violins sing. It is the swollen belly and the child within; the fervent kiss; the sound and motion of the violin players — these centers again are the real stuff of which the world is made, in our experience, in its emergent actuality. A gathered fistful of flowers, pushed into a jam-jar, then set upon a table — this is a center which gives the afternoon its meaning.

Are these several very different kinds of centers all of one kind? And is it reasonable, fair, accurate, to speak of a kind of wholeness which embraces all of them together? For reasons that are explained more fully in chapter 11, I believe that all centers that appear in space — whether they originate in biology, in physical forces, in pure geometry, in color — are alike simply in that they all animate space. It is this animated space that has its functional effect upon the world, that determines the way things work, that governs the presence of harmony and life.

But it is no small thing to see the world like this: a unitary source of organization, all of it anchored in space, with space itself the stuff that comes alive. That is the enigma. But it is also that which forms the effective substrate of the view I am presenting here, which gives us the possibility of understanding life at all.

14 / LIFE COMES DIRECTLY FROM THE WHOLENESS

The essence of the wholeness, as I have defined it, is neutral: it simply exists.

At each place in the world — with its natural habitat, ecology, buildings, materials, actions, and events — there is, at any instant, some given wholeness; that is, some definite, well-defined system of centers that creates the organization of that part of the world. And the wholeness always exists in some form, whether that place is good or bad, lifeless or alive.

But we shall see next that the degree of life which exists at that place and time also comes from the wholeness, and only from the wholeness. The neutral wholeness spawns characteristics which are far from neutral — characteristics which indeed go to the very origin of right and wrong. As we shall see in the next chapter, the life which occurs is specifically dependent on the system of centers, and the degree of life, the intensity of life, arises from the wholeness. Whether it is an apple-orchard, a dining-room, a harem, a dung heap in the garden, a painting, the wall of a building with its windows, the glaze of an earthenware pot, or the fervent kiss of a boy — in every case, the life which that thing has arises from its wholeness.

So — this neutral wholeness, which lies under the surface of every place, at every time, in buildings, meadows, streets — is the natural origin of life. Life comes from it. Life comes from the particular details of the ways the centers in the wholeness cohere to form a unity, the ways they interact, and interlock, and influence each other. The academic and difficult task of grasping the nature of this wholeness will pay us back, by giving us the origin of life.

NOTES

1. The general idea of wholeness, or relative wholeness, as the fundamental primitive, has been discussed by many authors, for example Jan Christian Smuts, HOLISM AND EVOLUTION (London: Macmillan, 1926); Wolfgang Köhler, GESTALT PSYCHOLOGY (New York: Liveright, 1929) and THE PLACE OF VALUE IN A WORLD OF FACTS (New York: Liveright, 1938); Kurt Koffka, PRINCIPLES OF GESTALT PSYCHOLOGY (London: Routledge & Kegan Paul, 1955); Gregory Bateson, MIND AND NATURE: A NECESSARY UNITY (New York: Dutton, 1979). It has been discussed most notably perhaps by Whitehead in PROCESS AND REALITY, AN ESSAY IN COSMOLOGY (Cambridge: The University Press, 1929).

2. For example, John Wheeler and Wojciech Zurek, QUANTUM THEORY AND MEASUREMENT (Princeton, N.J.: Princeton University Press, 1983); or David Bohm, QUANTUM THEORY (New York: Prentice-Hall, 1951).

3. For example, Charles Misner, Kip Thorne, John Wheeler, GRAVITATION (San Francisco: Freeman, 1975).

4. A piece of tissue, transplanted from a newt's eye, if transplanted to the tail, becomes a tail. A piece of growing tail, transplanted to the eye, becomes an eye. It is the larger configuration which determines the destiny of the growing material, not its local or internal structure. See H. Spemann, "Experimentelle Forschungen zum Determinations- und Individualitätsproblem," NATURWISSENSCHAFT 7 (1919), described in Ludwig von Bertalanffy, MODERN THEORIES OF DEVELOPMENT (New York: Harper & Brothers, 1962), 121-22.

5. No one spot in the brain holds a particular memory. Each memory is suffused throughout the brain, and is apparently global, not local. Karl Lashley, "In Search of the En-gram," PROCEEDINGS OF THE SOCIETY FOR EXPERIMENTAL BIOLOGY 4 (1950): 454-82, reprinted in F. A. Beach, D. O. Hebb and C. T. Morgan, THE NEUROPSYCHOLOGY OF LASHLEY (New York, 1960).

6. See J.S. Haldane, THE LUNG AND THE ATMOSPHERE AS A SINGLE SYSTEM IN ANIMAL BIOLOGY (Oxford, 1927).

7. Ernst Mach, DIE MECHANIK IN IHRER ENTWICKLUNG HISTORISCH-KRITISCH DARGESTELLT (Leipzig: Brockhaus, 1912).

8. James Lovelock, GAIA (Oxford: Oxford University Press, 1979).

9. The wholeness $W$ is fully defined in mathematical terms in appendix 1.

10. More detailed study of the geometrical and structural factors which make segments of space function as centers is given in chapter 5. In the literature the definition of these features which cause centers to stand out or "settle out" has, in the past, usually been thought of as psychological, and the study of these features has usually been considered as a branch of cognitive psychology. The fact that the level of wholeness of different centers is objectively given, and may in principle be determined, was described by the gestalt psychologists Max Wertheimer, Wolfgang Köhler and Kurt Koffka, who formulated the laws of "praegnanz" as the determining features of a whole, which gives it its strength. See Wolfgang Köhler, GESTALT PSYCHOLOGY (London: G. Bell and Sons, 1929); Kurt Koffka, PRINCIPLES OF GESTALT PSYCHOLOGY (New York: Harcourt, Brace, 1935). One of the most detailed accounts was given by Marian Hubbell Mowatt, "Configurational Properties Considered Good by Naive Subjects," AMERICAN JOURNAL OF PSYCHOLOGY 53 (1940): 46-69, reprinted in David Beardslee and Michael Wertheimer, READINGS IN PERCEPTION (New York: Van Nostrand, 1958), 171-87.

11. Entities appear in the world because different parts of space have different levels of coherence. In ancient times, one of the first writers to notice this explicitly was Chuang-tzu, who saw how the order of a piece of meat depended on the fact that some pieces were more knit together than others, and that "understanding" anything in the world consisted of grasping correctly the way that thing could be divided into pieces which are relatively more or less coherent. The butcher who hacks at his meat blunts his knife quickly. But the butcher who has attained wisdom presses his knife into the soft spots, the crevices of the meat, and almost makes the meat fall apart according to its own structure. This butcher keeps his knife sharp for a hundred years. The image of this butcher who sees the world as it really is, is fundamental to all Taoist texts. In modern times, the importance of coherence, and the relative coherence or wholeness of different entities, was first studied by Köhler and Wertheimer — who described the ways that collections of dots form groupings, and that some groups are more coherent than others. They formulated this idea as the laws of "praegnanz," or laws of coherence, which was their first attempt to state the laws which created relatively more and less coherence in different parts of space. See Köhler, GESTALT PSYCHOLOGY.

12. For years, I struggled with the idea that everything — all form — was made of entities. I first struggled with it in a lost manuscript, THE UNIVERSE OF FORMS (a manuscript written 1965-1967, and then unfortunately burned, without any copy being preserved). I had formulated a theory in which I tried to show how all order and all form could be understood by building things up from the coherent wholes which appear in space. Years later, in 1970-1975, I came back to the same ideas and struggled with them again in THE TIMELESS WAY OF BUILDING and A PATTERN LANGUAGE. In these books I showed how the significant relationships which appear in buildings are all patterns of wholes, and that once again it is the entities themselves which play the fundamental role. Alfred North Whitehead had formulated similar notions of "organisms" (his word for entities) early in this century. However, my attempt to catch the solidity of these entities as the fundamental elements of order never really came out right; it never worked as the fundamental notion. I began trying to get this straight in the later versions of A PATTERN LANGUAGE, where I noticed that even the entities which formed a pattern were in effect patterns, too, so that properly a pattern was not

a pattern of entities, but a pattern of patterns. This brought the entity concept into doubt by stressing the fact that the things which appeared to be entities were fluid, not fixed, not bounded, not really "things" at all. All this finally became clear to me about ten years ago when I finally understood that all these troublesome entities, which were so important as the building blocks of nature, were not truly bounded entities but were in fact non-bounded centers: Centers of influence, centers of action, centers of other centers — centers of some kind, appearing in the seething mass of the wholeness. About fifteen years ago, I finally realized that this way of looking at things was logically consistent, solved all the earlier problems of "entities," and was a solid footing on which a theory of order could properly be built.

13. One book which discusses the idea of centers in a fashion that has some kinship to my discussion here is Rudolf Arnheim, THE POWER OF THE CENTER: A STUDY OF COMPOSITION IN THE VISUAL ARTS (Berkeley: University of California Press, 1982). Another, much earlier work from the 18th century, which tries to establish point centers as the foundation of an all-embracing physics, was Roger Joseph Boscovich, A THEORY OF NATURAL PHILOSOPHY (London, 1763; reprinted Cambridge, Mass.: MIT Press, 1966).

14. The theory of fuzzy sets, put forward in topology by Christopher Zeeman "Tolerance Spaces and the Brain," in C. H. Waddington, TOWARDS A THEORETICAL BIOLOGY (Chicago: Aldine, 1968), 140-51, makes an attempt to solve this difficulty. However, in my opinion, it does not penetrate to the core of the matter.

15. Here we come back to Chuang-tzu again, and the difficult task of seeing the world as it really is, by seeing the entities in their proper order of saliency, not a distorted one. The same point has also been made forcefully by David Bohm, FRAGMENTATION AND WHOLENESS (Jerusalem: The Van Leer Jerusalem Foundation, 1976). See also appendix 3.

16. The structure is defined mathematically in appendix 1.

17. The idea of representing any given pattern as a system of selected coherent sets also appears in the foundations of topology. A particular topology is defined by the way in which the coherent sets are nested. But in this case, the definition of "coherent set" is much more restricted and less interesting. The fundamental idea expressed in this book is that the levels of coherence of different sets of centers may be continuously variable, and defined by much more subtle criteria. See appendix 1.

18. Concepts presently available to us in mathematics are not yet powerful enough to let us grasp this structure fully. For this reason many of the techniques, tests, and methods which I describe in this book are cognitive. The empirical methods which are described in this book (chapter 9) are the best I have been able to develop to get to grips with the structure.

19. Henri Matisse, "Exactitude Is Not Truth," first published in HENRI MATISSE: RETROSPECTIVE (Philadelphia: Philadelphia Museum of Art, 1948), reprinted in Jack D. Flam, MATISSE ON ART (New York: Dutton, 1978), 117-19.

20. My understanding of this point has been enlarged very greatly by conversations with my daughter Lily. It was not until she explained it to me, by drawing her own sketches of people and telling me how she saw, and was able to catch, this underlying character in a person, that I really understood this short essay of Matisse, even though I had been studying it for years.

21. A key formulation of this matter was given by Niels Bohr, the father of quantum mechanics, who said that we can only understand the behavior of the electron in this experiment if we understand that, somehow, the electron moves as a function of the entire experimental setup. Niels Bohr, "Discussion with Einstein on Epistemological Problems of Atomic Physics," first published 1924, reprinted in Wheeler and Zurek, eds., QUANTUM THEORY AND MEASUREMENT (Princeton, N.J.: Princeton University Press, 1983), 30.

22. One coherent account of this phenomenon, and one which directly approaches the structure I define as the wholeness, is David Bohm's WHOLENESS AND THE IMPLICATE ORDER (London: Routledge & Kegan Paul, 1980), where he also describes the underlying structure of space that determines the path of the electron. In a series of meetings between the two of us, held in Ojai, California, in 1988, Bohm told me that he believed what he defines as the implicate order, and what I define as the wholeness, are essentially one and the same thing. This is also discussed more fully in appendix 5.

CHAPTER FOUR: HOW LIFE COMES FROM WHOLENESS

1 / VITAL POINTS

From chapter 3 we have the idea of the wholeness as a neutral structure that exists in every part of space. Wherever we are in the world, there is a wholeness. Each wholeness, at whatever scale, is made of centers: the coherent entities which appear in that space, and the way they overlap. To form a wholeness the centers are rank-ordered by their degree of coherence. Mainly the wholeness is formed by the top centers, the most salient centers.

We do not yet have a clear idea of degrees of wholeness, degrees of life: how one thing comes to have more life than another. The key idea in this book is that life is structural. It is a quality which comes about because of the existence of a discernible structure in the wholeness—and therefore explains what we perceive as the quality of buildings and artifacts. The structure is something I shall later define as “living structure.”

This chapter will show, in detail, how life actually occurs because of wholeness. Somehow a kind of conjuring trick is done, almost as if spirit appears out of matter and space.¹ But it is not a trick. What I would like to demonstrate is the way that the creation of life is possible, and how it is done. There are four key ideas, all arising from the structure of centers described in chapter 3:

1. Centers themselves have life.
2. Centers help one another: the existence and life of one center can intensify the life of another.
3. Centers are made of centers (this is the only way of describing their composition).
4. A structure gets its life according to the density and intensity of centers which have been formed in it.

These four points, simple as they are, give us the secret of living structure, and of the way life comes from wholeness.

2 / THE HOTEL PALUMBO

To start the discussion, I am going to describe a particular place which I like very much. In this example, we shall see that the wholeness in a part of space gets more life, or less life, according to the way the centers help each other. When centers help each other the wholeness has more life: when the centers are not helping each other the wholeness has less life.

A few summers ago my family and I went to Ravello, a few miles south of Naples, high above the Mediterranean, looking down over the Bay of Salerno. We stayed in a small hotel, the Palumbo, first built as a palace in the 11th century. One of my favorite places in the hotel was the garden and terrace overlooking the gulf. The bay is soft blue, there is a perpetual haze, so that the blue of the sea and the blue of the sky are not divided and one looks out into a pale blue sphere of light. The hotel garden is quite small, filled with flowers, and has a lovely terrace right at the edge

of the cliff. If we asked for it, our breakfast was brought out to this garden, which we had quite to ourselves. Every morning we sat there for hours having our coffee, watching the gulf, while the children played among the flowers of the garden and tried to catch the lizards.

Following is a partial list of a few of the centers which formed the wholeness of this terrace. First are the architectural centers which are created in the geometry:

• The bays formed by four columns

• The individual spaces of these individual bays

• The big white columns

• The repetition of the bays

• The trellis of rounded branches

• The nine parts of the trellis

• The capital of the column

• The base of the column

• The chamfer on the corner of the column

• The balustrade wall between the columns

• The slight camber on the columns

• The cap of the balustrade

• The electric light on the columns

To complete the picture, we must add other equally essential, but non-architectural, centers:

• The individual tables and chairs
• The grass of the lawn in the bays
• The grapes growing on the trellis
• The stem of the grape vine
• The view of the gulf through the columns
• The visits of the waiter, bringing coffee
• The coffee cups on the tables
• The vines growing on the columns
• The blue shimmering sea beyond the cliff
• The filtered sunlight dappling the grass

This describes a few of the hundreds of centers which together form the wholeness of the terrace.

3 / HOW LIVING STRUCTURE IS CREATED FROM THE CENTERS IN THE WHOLENESS

It is hard to deny the life of the Palumbo Hotel terrace. The life of the place is tangible and immediate. But this wonderful life does not come about merely because of a vague beauty in the place. It comes about in a very definite way because of the centers in the wholeness and their relation to one another. In particular, it comes about because the different centers help each other.

It is this mutual helping among the centers which causes the life and is the crux of the whole thing. Here is one example of this "helping" between centers: The terrace is made of structural bays — each made by four columns — each roughly square, about 13 feet by 13 feet. Each of these bays is itself a center. At the corners of the bays there are columns. The columns are centers, too. And on each column, on each of its corners, there is a chamfer. The chamfer is once again a center in its own right.

Each of the four-column bays is helped to be alive by these tiny chamfers on the columns at the corners of the bay. What I mean by this is that each bay becomes more of a center, and is more alive, because of the chamfer. Suppose, for example, that the columns had been made square, without the little octagonal chamfer on the corners. Then, as you can see on the facing page, each column would slightly eat into the space of the bay, thus disturbing the wholeness of the bay. Instead, the four chamfers help, geometrically, to increase the unity and wholeness of the space in the bay. These chamfers, which are only two or three inches across, strengthen and intensify the structural bay which is created by the columns, and is some 13 feet across. At the same time, the chamfer also helps and intensifies the column itself. Thus we have the following helping relations between the space, the column, and the chamfer:

4 chamfers - column 4 columns - space of bay 16 chamfers - space of bay

Each bay has a system of twenty-one centers, in all, each getting life from the presence and cooperation of the others.

It must be emphasized that this helping relation between centers does not occur automatically. The columns could just as easily have been made in another way which would not have this beneficial effect on the space. The corner of the column could have been given a shape which does not help to intensify the column. Creating a smaller center (in this case the chamfer) which successfully intensifies the column and also intensifies the bay (space made by four columns) is quite a trick.

Let us look at another case. In the lower left-hand photograph, the children are playing in the small walled garden at the end of the terrace. The walled garden continues the space of the terrace, but encloses and "ends" it. The beauty of this closing is not only geometrical. As you can see, the children run the length of the terrace, then turn around in the end part, and come flying back. An old person strolling along would do a slower version of the same. The garden at the end, by forming a turning point, helps the terrace as a whole, makes it more of a living center than it would be without it. Again the result is not automatic. If the garden at the end

were smaller, or larger, or differently walled, this effect would not occur.

Another example. There is an electric light mounted on the column, a very ordinary light that was chosen and placed so that it helps the capital. The capital becomes a little more intense because the lamp is just there. Again, this is not automatic. If the light were lower down, or asymmetrically mounted, or a more obtrusive shape, this would not happen.

In each case, the helping relation between two centers, A and B, may be seen in the fact that the one center increases the life of the other (the life of A helps increase the life of B). For example, when I look at the flower box on the low wall, the life of the low wall is increased by the existence of the flower box. If I take the flower box away mentally (with my hand, by covering part of the photograph) I see the life of the low wall drop down, diminish.

Although, in one sense, the helping relation between centers is obvious, you may be puzzled as to how one might determine, operationally, when one center is helping another one. Wouldn't it be possible to say that any two centers near each other are helping each other? How do we know when it is really happening? This quite reasonable question has a practical answer. Suppose we have two centers A and B, and we want to know if B is helping A or not. We simply

look at A with B, and without B, and go back and forth between the two, using the criterion of life to decide which of the two, A with B or A without B, has more life. If, of the two, A with B has more life, then B is helping A.²

In this terrace at the Hotel Palumbo there are dozens—hundreds really—of these helping relations between the centers. Here are some other examples:

• The capital of the columns is shaped to make the columns more alive.

• The nine-fold division of the trellis helps the bay become calmer and more alive.

• The tables set in the bays help the bays come to life.

• The bays also intensify the tables.

• The low wall between the columns intensifies the column bay between the water and the garden.

• The low wall helps the view.

• The view of the bay and the blue sky helps the individual bays.

• The grapes help the view.

• The grapes help the tables.

• The round tables help the bays.

• The chairs help the round tables.

• The lights on the columns help the columns and the bays.

• The flowers in the garden help the bays.

• The low wall helps the flowers.

• The grass helps the terrace.

• The vines help the grass.

Some of the helping relations between centers are very large in scale. For example, one of the most important centers in the terrace is the view through the columns. Certainly at the Palumbo it is one of the most marvelous things: a vast entity extending out from the terrace towards the distant hazy blue of the sea. We

may imagine it as a cloud of space stretching from the terrace to the sea and over the sea. In a person's experience of that place, there is no doubt this center appears as a major entity, and no doubt that the existence of this large center brings life to the smaller center of the terrace itself.

What makes us so definite about recognizing the merging of the blue of the sea and the sky as a center in the place? It is something we are transfixed by, we stare at it, we are drunk in

it, and the far-off blue haze helps the green vines of the terrace come to life. And the bays of the terrace themselves, as individual centers, gain greater life from this larger center which is stretched between these bays and the world beyond towards the Gulf of Salerno.

The system of centers, the ways these centers help each other, and the continuity of the thing with the whole world—these together form the structure which establishes the life of the thing.³

4 / RECURSIVE DEFINITION OF A CENTER

We need to go back to the key question in the puzzle of wholeness: What exactly is a center? This question holds the key to the problem of order, and to the entire problem of living structure.

The crux of the matter is this: a center is a kind of entity which can only be defined in terms of other centers. The idea of a center cannot be defined in terms of any other primitive entities except centers.

We are used to a view where we try to explain one kind of entity by showing it to be constructed of other different kinds of entities. An organism is made of cells, an atom is made of electrons, and so on. All of these are centers. If we ask what the centers are made of, we come up against a brick wall. Here we have a question

so fundamental that it cannot be explained or understood, as a composite of any other more fundamental kind of entity. Instead, we shall see centers are only made of other centers. This is the most fundamental concept. The nature of these centers can therefore be understood only reflexively, or recursively. This is one reason wholeness looks so mysterious to those who are wedded to mechanistic thought.

Consider, for example, the apple tree shown on the next pages. I see the tree as a center, I see its branches as centers, the blossoms as centers, and the petals of the bloom as centers. The fact that I can see the tree as a center comes about because I see it as a whole: seeing it as a

whole, I see it made of other centers, branches, which I can pick out and identify, again, because I see them as centers, too.

The wholeness of the tree, as I see it, comes from the way that I understand the interpretation of these many centers: by recognizing that the tree is made of branches. My ability to perceive that a branch is a center is necessary part of my ability to see the tree as a center. I cannot find some way of explaining the centeredness of the

tree which does not rely on my ability to see the centeredness of the branches.

This interconnection of my perceptions goes all the way to the very bottom of the foundation that my perceptions stand upon. Consider, for instance, one of the apple leaves shown below. We feel it to be a center, of course. Now, suppose I ask what it is about the leaf which makes it seem like a center. To answer this question, I have to point to the tip of the leaf, the uniform double curvature which makes it a single thing, its spine, its minor ribs, all parallel to one another, the zone of flesh roughly a parallelogram between two ribs, the stem of the leaf, and the indentation where the leaf is joined by its stem, and the very tiny serrations, almost smooth, which form the outer boundary of the leaf. All these are centers.

It is the organization of these centers which makes the whole leaf a center. Yet all these things are themselves centers. That is why we notice them. It is their centeredness which we notice,

and which makes us pick them as the elements with which to see and explain the centeredness of the leaf as a whole. Thus it is the organization, the "centered" organization of these other centers, which makes the leaf a center in our experience. As soon as we try to describe, precisely, why this particular thing is a center, we find that we have to invoke some kind of description in terms of other centers.

In mathematics, such a concept is called recursive.4 Grasping this idea, and grasping the fact that this bit of understanding is a positive step forward, and not problematic, is the key to understanding wholeness. The apparent circularity here is — I believe — the crux of the prob-

lem of wholeness. The reason that deep wholeness (or life) is so mysterious, is that centers are built from centers, wholeness is built from wholeness.5

This is not a peculiarity of the leaf. It is typical of every single thing in the world that we can examine. In fact, it is precisely this which I believe to be unavoidable. What then is a center? A center is not a primitive element. Centers are already composite. Yet they are the most primitive elements available. They are bits of wholeness which appear as structures within the wholeness. But where do they come from, and what are they made of? The answer to this question is essential to all that follows.

Centers are always made of other centers. A center is not a point, not a perceived center of gravity. It is rather a field of organized force in an object or part of an object which makes that object or part exhibit centrality. This field-like centrality is fundamental to the idea of wholeness.6

The relative wholeness or centeredness of any given center can only be understood in terms of the relative centeredness of its component centers and their organization. There is no way of describing the centeredness of a leaf—or anything else—which does not invoke the centeredness of its various component parts, and of those around it. If I try to explain why a given thing feels like a center—why a center occurs at a particular point in the organization of the leaf—I cannot avoid talking about the other centers which occur at other levels. The centeredness or centrality in the leaf comes from the organization and interplay of its centers, and they are only centers because of their organization and their relatively greater centeredness.

So there is a fundamental circularity which we cannot escape. This circularity is not a mistake, or an indication of something logically vicious in the argument. On the contrary, it is the essential feature of the situation. Our understanding of both wholeness and life will come into focus just at that moment when we thoroughly grasp this circularity and what it means.

5 / THE DIAGRAM OF LIVING STRUCTURE: EACH CENTER AS A FIELD

To understand the idea of a center and its recursion deeply, it is necessary to learn to see each center as a field. What makes a center "centered" is that it somehow functions as an organized field of force in space. It has a structure of centrality, it communicates centrality, it creates a spatial feeling of centrality.

To see how this comes about, I should like to ask that you examine the ornament shown below. It is a fragment from a 15th-century Turkish carpet (shown on the next page) whose beautiful design is made of centers, perhaps more visibly than other examples I have asked you to consider. I have picked out just one of the centers in this carpet and show it, below, in black and white. Next to it, I have drawn a diagram of the field-like living structure which creates this center. This field-like structure may be visualized something like a vector field (see note 7). Each part of the field points in some direction, towards some other center (see the diagram). Here we see wholeness, not merely as a nested system of centers (as in chapter 3), but as an ordered system in which the way that different centers and subcenters help each other creates the field effect. What do the arrows in this drawing represent? They are orientations created by the contribution

which centers make to one another. These orientations are also centers. Thus the elements of the field are both centers of different strengths, and helping relationships among centers. Together they create a structure, not unlike a vector field, but with many layers hierarchically ordered.

The diagram shown is a map, if you like, of a typical center within a living structure. It shows how the whole ornament, as a field, creates a feeling of centrality. In the ornament there is an organized field of force which organizes space and creates an overall impression of something centered. As such a structure becomes more dense and more complex, it approaches the thing I call living structure.

Let us go back to the definition of wholeness. Let us imagine a space as filled with centers. As part of the definition of wholeness in chapter 3, I suggested that centers arise from certain sets in space — often bounded, connected, convex, often symmetric, differentiated from the space next to them — and radiating outward and creating coherence through a centered quality in space. But this is a convenient simplification.

To be more realistic, we need to imagine space as filled with such centers, all helping each other, all created by other centers, but all field-like, all radiating centeredness. How might we imagine this structure? We may imagine, in this space, an overall field in which, at each point there is an intensity — the life of that field at that

point—together with vectors describing the impact of these centers on one another.

How can we describe it? Well, each of the new structures we observe is "induced" within the field as a new center of some kind. There are the centers between other centers, centers along the arrows, the arrows themselves, which themselves exist as centers, and so on. The ornament creates a structure which is, in some fashion, a continuous distribution of centers.

We may summarize the action of this field by means of a definition which is explicitly recursive: Each center is a field of other centers. By this definition, each of these other centers must then also be a field of centers. Thus a center is a field of centers, and within that field each center

is a field of yet other centers. There are no ultimate elementary components of the field, except the centers themselves.⁸

This is the foundation of what I mean by living structure. It would be very helpful to have a general mathematical description of this kind of field. But in its hierarchical ordering and in its great complexity, it is so unlike the structures conventionally used in present-day physics and mathematics, that it is not easy to grasp the nature of such a structure, let alone to represent it formally as a well-defined field of a new kind.⁹

However, we may say this: in many of the examples shown, the key centers are symmetrical. Indeed, to a first approximation, one may identify the centers in a field as emanating from those entities which are convex, bounded, and roughly symmetrical, and differentiated from their surroundings.¹⁰ Some centers roughly follow these rules. But the rules are only approximate. A few of the centers and subcenters which appear in the carpet ornament are shown on the right. Some are imperfectly symmetrical. Some are not convex. Some are mainly defined by the degree to which they are differentiated from their surroundings, not by symmetry or boundedness at all. Nevertheless, as a rough rule of thumb, we may keep hold of the idea that centers are coherent entities, often marked by local symmetry, by differentiation, by the presence of a boundary, and by convexity, which cooperate to cause a field effect.¹¹

The mathematical definition of such a field awaits the work of other investigators. But no matter what the mathematical results, I believe it is true to say this much: there is no way of defining the field in terms of ultimate elements that are essentially different from centers. There are no elementary entities that every center can be made of except other centers. The apple leaf on the apple tree occurs as a field of centers. The terrace of the Palumbo Hotel occurs as a field of centers. Each is a recursive field effect in which centers are induced by other centers. This is the basis of the phenomenon I shall now go on to describe as living structure.

6 / EACH CENTER HAS ITS LIFE

Armed with the idea that each center is a multi-levelled field-like phenomenon made of other centers, let us now come back to the idea that each center has its degree of life.¹²

The idea of this life of an individual center is similar to the idea already expressed earlier, that any given part of space in the world has its degree of life. But I want now to extend this idea and apply it separately and individually to every distinct center in the wholeness of a thing.

I simply assert (without, for the time being, demonstrating it) that every center has a distinguishable degree of life. If we accept this assertion, we may see how the degree of life of each center in a given wholeness depends on the degree of life of all the other centers in the wholeness. To get this, I propose to use the following unusual way of thinking, even though it may seem different from our normal ways of thinking.

I make five assertions:

1. Centers arise in space.
2. Each center is created by a configuration of other centers.
3. Each center has a certain life or intensity. For the time being we do not know what this life "is." But we can see that the life of any one center depends on the life of other centers. This life or intensity is not inherent in the center by itself, but is a function of the whole configuration in which the center occurs.
4. The life or intensity of one center is increased or decreased according to the position and intensity of other nearby centers. Above all, centers become most intense when the centers which they are made of help each other. Exactly what "helping" means in this context remains to be defined.
5. The centers are the fundamental elements of the wholeness, and the degree of life of any given part of space depends entirely on the presence and structure of the centers there.

From these five assertions, it will follow that the life of a given part of the world depends on the structure of centers it contains — and that these centers are given their life, in turn, by the way that each one is made of still other centers. The interactive effect lies in the fact that each center has the power to intensify the life of other centers, and that the life of any one center comes about as the result of the placing and relative degrees of life of other nearby centers.¹³

7 / EACH CENTER GETS ITS LIFE FROM OTHER CENTERS

Consider the beautiful room from the Alhambra, illustrated here. In part, the beauty of the room depends on the life of the wall surface. Let us examine the life of the tilework forming wall surface. On the following page, there is a photograph of a tile fragment, which comes from one of these rooms in the Alhambra, where a whole wall was covered with this pattern.¹⁴

When we look at the pattern on the tile fragment, we see many different centers. A black star, a black star-octagon, a green hexagon, the white space between the green hexagons, the very small white diamond between adjacent pairs of the black hand-shaped figures — they are all centers. And they all help each other.

To understand exactly how these different centers help each other, it is necessary to pay careful attention to the life of all the centers, each one in its own right, and then as they begin to work together. In looking at these examples, one must pay acute attention to one's inner feeling in order to judge the degree of

life in each example, to see how it is changing.¹⁵ Let us begin with the black eight-pointed star. Look at the five diagrams in the first sequence. In each case we see a center. But the centers, as drawn, become progressively more intense in their life as we go down the sequence from top to bottom.

Step 1. Star shape, alone, without color. It has a certain life, but is limited.

Step 2. Star shape, colored black. When the star is colored black it is more intense than when it was white, because it is now more differentiated from its surroundings.

Step 3. Now we add tips at the points of the black star. This is more lively because it is supported by extra centers at the points of the star.

Step 4. Black star with partly formed white pentagons between the rays of the star. This figure is even more intense, because now the spaces between the arms of the star are working as centers, too; the whole thing takes on more life than before.

Step 5. Finally, a star which is still more intense, because the black hand-shaped figures have been added, together with the small white diamonds between them. The double system of more elaborate centers stretching out from the arms of the black star adds even more; the life of the figure is still further intensified.

In this progression, the star obtains progressively more and more life. Even if you are not sure why the stars in the five illustrations have progressively more and more life, I think you will agree that they do have it.

Let us look at the same thing on a more sophisticated level in the pattern of four green hexagons which form a cross that surrounds the black star-octagon. At the core of the pattern,

there is a black star-octagon. It is shown first by itself. This black star-octagon has some life as a center, even with nothing around it. This star-octagon receives additional life as a center from the other centers near it. For example, if I cover

Step 1: The black star-octagon, with nothing around it

Step 2: The black star-octagon, intensified by four green hexagons stretching out from it and forming a cross

Step 3: The four green hexagons around the star, together with the four white "shirt" shapes and the four little white diamond-like lobes

Step 4: The four white shirts and the green hexagons, together with the larger fishtail shapes that extend beyond the hexagons and intensify the black star-octagon still further.

everything in the pattern around the star-octagon, except the star-octagon itself, its life is much diminished. As I open my hand, and gradually reveal more and more of the surround-

ings, the center formed by the black star-octagon regains more and more life.

Step 1. The black star-octagon by itself.

Step 2. Next, we see the four green hexagons around it, but without the white space between them. The center formed by the black star-octagon gains life when it is supplemented by the arrangement of the four green hexagons.

Step 3. To the four green hexagons are added the four white "shirt" shapes between them, and, in addition, the four little white diamond-like lobes which extend out from the shirts. The center becomes stronger still, and its life increases again.

Step 4. Now we see the larger diamond which contains the black star-octagon plus the four green hexagons and four white shirts, with the four white fish-tail shapes and the large dark octagon edges beyond them. The center gains even more life.

Step 5. Finally I open my hand completely and let myself see all the structure which surrounds the star-octagon, and the complex structure which surrounds the more distant black eight-pointed star as well. The centers now acquire even more life.

We begin to realize how within the tile fragment the center which seems localized in the

Step 5: The complete pattern, as it appears on the original fragment. Here we see the additional impact of the neighboring pattern of the black eight-pointed star, and the centers surrounding it, and what all this does to increase the life of the star-octagon yet further.

black star-octagon actually extends outward several inches, and how it grasps the space, even as far out as the black star, and interacts with it. When we understand this, we see the whole fragment as more remarkable. Our respect for the builders of the Alhambra increases greatly, and our understanding of the center formed around the star-octagon grows.

8 / HOW LIFE OCCURS WITHIN A BUILDING

What we have in general, in any configuration, is a state of affairs where each figure has the character of "being a center" to a certain level of intensity. The more intensely it has the character of "being a center" the more life it has. But this intensity is not a local phenomenon. It is determined by the way this one center sits in the system of other centers, the density of these other centers, and the degree of life these other centers have.

Thus we have a complex reciprocal relationship. Various zones in the pattern become centers because of their position and character within the pattern. This in turn depends on the relative position and intensity of other centers that spring up all around. Yet that in turn may depend on the life of the original center, since it also helps to determine the life of these others, which support it. All in all we have a bootstrap relation, in which no one center is the origin of the structure or its life — but the various different centers all support each other mutually. Their life arises mutually as a result of the way the centers prop each other up. No one of them comes first; each helps to support the others. Together they all raise themselves to life.[16]

This conjuring trick is something akin to the trick of making Frankenstein. We take dead matter, rooted only in space endowed with the

rules governing the interaction of centers, and it can then raise itself to life.¹⁷

Let us apply this kind of thinking to a more ordinary part of a building. Compare the three doors on these facing pages. One is a typical hollow-core plywood motel door. The main center is the door itself. Its life is almost nonexistent. What little life it has comes, most of all, from its rectangular shape. Like any rectangle, it gets its centeredness from its edges and the corners. The edges also exist as centers—they are formed by the straight cut along the edge—and the centers that we recognize as edges are intensified by the centers which exist at the corners. The thin frame weakly helps the life of the door. It is made of centers (the trim pieces), and the placing of these trims make the main center a little stronger as a center. The handle also helps. But the overall effect is extremely weak.

Next, we see a more elaborate Georgian door in London. Here the two centers formed by the wide panels on either side strongly intensify the main center. So does the half-circle of the window over the door. The half-circle is itself intensified as a center by the rays of which it is made. The subdivision into rays strengthens it as a center and gives it more life, and as a result it then passes on more life to the door below. The panels of the door intensify the main center of the door; these panels are again subsidiary centers, placed there for this reason. Each of these panels is itself intensified by the trim and molding along its edge. And of course, the larger centers, outside the plane of the door, also make a big difference in bringing it to life. The steps are centers which bring the stoop to life; the center which the stoop forms brings the door to life. The path leading to the stoop brings more life to the stoop and

subsequently to the door. The balcony over the doorway completes the larger volumetric center of the door, and intensifies its life still more. It is clear that the Georgian door has more life than the motel door, and that this will be experienced as a more living environment by the people who live there. This is because the Georgian door receives more life from its component centers, partly because there are simply more of them, but mainly they are better arranged, and they also have more life as individual centers, and are placed to contribute more life to one another.

It must be stressed that a center does not get more life merely according to the number of its subsidiary centers. Such an idea would only lead to the fallacy of baroque architecture which piles on detail, but which never reaches a very intense kind of life. The Nubian door is an example of a very simple door which nevertheless gets enormous force as a center,

not from detail, but from very, very careful choice of shape, voids, and proportions, combined only with a tiny bit of detail. It is simple, not elaborate at all. Yet as a center it is more powerful than the Georgian door. This comes about because the centers are more carefully chosen for their intensity. Each center is in itself more intense, and the arrangement of the centers — few as there are of them — is calculated to make the larger centers as intense as possible. Though less worldly, it has more fire.

We see then, that the life of a center — even in a simple door — depends on the configuration of component centers, and to the wider system of centers which appears round about it. Life comes from the wholeness, from the system of centers. The degree of life attained comes from the degree of life of the component centers, and from their disposition.

9 / HOW RECURSION, AS A PROCESS, CREATE THE LIFE OF A CENTER STEP BY STEP

In six steps we will build up a center, step by step, recursively, gradually introducing other centers to intensify the field effect and create the center's life.

Step 1. The column as a center. Start, let's say, with a simple eight-foot column, 9 inches in diameter, supporting a porch roof. For simplicity's sake we start with a round column, unadorned, without either base or capital. The cylinder of this column forms a center in the crudest way. It has a compact shape, and is symmetrical, but that is all. There isn't much of a field there.

Step 2. The space next to the column as a center. We ask, now, how we can modify this center, by a system of centers which will intensify its field. First, let's try to create centers in the space next to the column. When the column is round, the space next to the column is shapeless, and doesn't work as a center. If we want to make a center in

the space next to the column, we must shape it better. One way of doing this is to make it more compact and more convex, by making the column square, instead of circular. Already it is slightly better.

Step 3. Centers at the top and bottom of the column. Now let's make the base of the column into a center. To do this we bring the foundation up out of the ground to form a base. And let us imagine that the beam which will sit on top of the column joins the column in something which is also a center, perhaps a little platform on top of the column. We now have introduced some smaller centers.

Step 4. Making top and bottom unequal. But now the whole has lost its quality as a center, so we must adjust what we have done to restore the feeling. If top and bottom are equal, the feeling of centeredness disappears. We make the top

smaller (lower) than the base. Then the feeling of centeredness comes back into the column we started with.

Step 5. Adding an ornament within the column, to intensify its life. Now we have created a complete system of centers that roughly corresponds to the kind of thing one can achieve within the confines of the recursive definition.

Let us try and extract, from the example of the column, the essentials of what is occurring in the field. Each center is created, and intensified, by the existence of other centers. So, we try to modify the column, by adding structure which will intensify the simple center which is the column. We do this by adding other centers. But we add the other centers very carefully to be sure that they work to intensify the center of the column.

Once we have done this, we have more centers than before. We have an emerging field of centers. The process is not additive: it is trans-

formative. At each step, we do not add things, but transform the previous version, as a whole, to give it more centeredness, as a whole, by inducing more centers to intensify those that exist already.

We apply the same thinking to each center in this field, recursively. We try to make each new center more definite, more truly centered, by adding yet other centers, which together increase centeredness. We do this without a very precise definition of wholeness or centers. There is nothing remarkably subtle about the capital, or the base, or the tiles we put on the ground. Yet each of these things intensifies the center which exists in the column, so that it becomes better and better.

During the recursion, it is not only the column which is getting better. Our understanding of what a center is, is also getting better. As we see the build-up of centers in the space, we gradually get a more developed idea of the kind of struc

ture needed in order for something to be a center. So the impact of the recursion is not only on the emerging column, but on our understanding.

At a certain stage, we recognize that the beauty and wholeness of the column itself is deeply affected by the wholeness and beauty of the space between the columns. We realize that the space between the columns can be understood as a center with its own shape, and its own substance—itself dependent upon all the subsidiary centers around it. And we find out that the nature of the column—its wholeness, its centeredness—actually changes qualitatively, as the space between the columns becomes more whole.

This is a great shift in understanding. An untutored person looking at a column will not understand that the column itself—its life—depends on the life of the space between the columns. These would be thought of as two separate things. It takes a big leap to realize that the

shape of the space between the columns not only helps the columns, but actually changes them, and that the wholeness of each column depends on the wholeness of the centers in the space between. They are not merely next to each other. They are interdependent. This leap of understanding is similar to the change I get, as a painter, when I realize that a certain beautiful green, with red spots on it, is an entirely different green from the same green paint without the red spots. At first, one is inclined to say that the green is the same green, and that the red spots on it interact nicely with it, or make a beautiful composition. But this is naive. As I grow up as a painter, I learn that the green itself—the actual substance of the green, is irrevocably altered when I

put the red spots on it — and that if I want to get that green I cannot get it without these red spots that become part of it.

This is the kind of change which happens in the column. As more and more centers are added to the column, the center which the column "is"

itself becomes intensified, and altered, and then intensified and altered again and again, as we develop the centers more and more. It is not the same column "with" some nice extra stuff around it. As a center, it is a different structure altogether.

10 / PROFOUND LIFE WHICH CAN ARISE IN THE DEEPEST CASES

A mature artist will use much more powerful and subtle ways of making centers and intensifying them in a building. Consider, for example, the great columns in the Temple of Hera at Paestum (below and next page). Here, in

making the space between the columns strong, a far more subtle approach is used, in which these centers (the spaces between the columns) become almost like solid bodies, they are so powerfully shaped.

Second, the swelling of the column itself (its entasis) creates a shape which intensifies the body of the column itself as a center, and also creates a powerful second center, within the body of the column, at the point where the column is most pregnant. The next detail which helps to make the column more powerful is the system of flutes, which cut into the surface of the column, creating a ring of new centers round the column. The column base is more solid, and because of its own hierarchy of centers, even a more powerful center, thus intensifying the column further. The metopes in the beams between the columns, because of their own center-forming power, intensify the beams, which again intensify the columns even more.

We could go on and on. The main point is that a mature artist can use the recursion of living centers in a very powerful way, thus creating centers which have still more life, which extract far tougher and more profound life from one another, and which create, overall, an even greater intensity.

The field of centers is not just a nice way of talking about ordinary structures. In its intense forms, an extraordinary structure, comes to life because of its dazzling and intense structural density. The more the centers are packed and overlapped to fill the space—the more an object is differentiated to produce center upon center, each one helping and intensifying the others, the more it comes to life.

11 / OBJECTIVE COMPARISON OF DEGREES OF LIFE

It is useful to bear in mind that the strong centers which occur in a living structure are not only "great," as at Paestum, but also down-to-earth and practical. Consider, for instance, a pair of houses. One is a traditional village house from Northumberland in England. Simple as it is, it is an inspired and profound center. The other is a postmodern house by the architect Charles Gwathmey from New York. It is rather weak in its life.

The Northumberland house is austere, perhaps not very warm inside when it was built. It even has corrugated iron on the roof. Yet every single part is a profound and living center in an ordinary and practical sense. The windows are profound centers. The chimneys are centers. The stones of the wall, individually, are centers. The door is a center. The roof is a center. The chimney pots are centers. The pieces of the wall between the windows, framed by the windows, are big centers. Even the rills in the corrugated iron function as centers. Even the wide piece of wood on the side of the window frame is a center. Each individual element, and every single part of the wall, is a strong center, with its own life. In this building we come close to an affair of the heart.

Compare the Gwathmey house—a postmodern building from the 1970s. Hardly one center is visible, and those few that do qualify

as centers would have to be called strained and very, very weak. The planks of the siding do not form centers. The arbitrarily shaped roof is hardly a center. The round thing coming towards you, though meant to be a center, is extremely weak because it is not sustained by any other centers. The column on the right is not a center. The entrance is not a center, just a big black hole. The space in front (driveway or lawn) is not a center, just empty space. The building is a series of abstract shapes, with almost no developed centers—and as a result, has little life.

This is not a matter of style—which it at first seems to be—but a matter of substance. In the space around the postmodern building, very little can happen because there are very few centers. The absence of centers guarantees a kind of deadness in the exterior space around this building. As far as one can see here, the absence of centers continues to the inside. The strange roofs and windows reveal an organization of space which is probably dead inside too. Indeed there are few centers inside, and there are few centers outside. The building will not have ordinary life.

The Northumberland house is not some quaint, romantic village antique. It is a more

robust structure, by far, than the postmodern house. It has living structure, solidly and deeply built throughout its fabric. However one may judge it, and however one may judge what we

architects should do today, this fact must be respected. Sneering at its depth of structure as a possible goal, as some contemporary architects have done, is a profound mistake.

12 / BREADTH OF THE CONCEPT OF LIVING STRUCTURE

The most basic aspect of the concept of living structure as I have described it is the great range it covers. (In chapter 7, I shall describe how functional problems in buildings are themselves solved, and supported by centers, so that the concept of life is deeply functional, not merely geometric.) However, it is useful to understand, from the beginning, that all systems in the world gain their life, in some fashion, from the cooperation and interaction of the living centers they contain, always in a bootstrap configuration, which allows one center to be propped up by another, so that each one ignites a spark in the one it helps, and that the mutual helping creates life in the whole.

Familiar examples abound in ecology: in the system of reeds, shallow water, insects, and water

at the edge of a lake, as shown below. Another example, rather famous from agriculture, is the fruit tree guild.¹⁸ Different species of trees mutually affect one another's health. Acacias help apple trees to be vigorous and healthy; mulberries also help apple trees. The presence of walnut trees, on the other hand, have a negative effect on the health and productivity of apple trees. Plants on the ground, including comfrey, clover, iris, and nasturtium, all have positive effects on apples trees. Thus when acacias and mulberries are planted together with apples, these centers have a positive effect on each other.

The concept of life or living structure — as something caused by the density of living centers in any given wholeness — explains life and function in a large variety of cases, cases so different

that, under other forms of analysis we currently know, they would appear unrelated.¹⁹

In the remainder of this book, in chapter after chapter, I have assembled a very wide variety of unrelated examples to remind the reader of the truly enormous scope the concept of living structure has, and how remarkable it is that this living structure, in this wide variety of cases, is created again and again, by the recursion of centers which produces unity.

As a dramatic and beautiful archetypal example we may look at the group of fishermen washing and mending their net. Of course, the life in this group of men, at this one instant, might be described in many ways, for instance in their thoughts and feelings, matters that are not visible in this photograph. But the life they share and experience is deeply correlated with, and cannot be separated from, the geometry of the system they are part of, with the existence of

smaller and larger centers, pervading their bodies, the scene, the sea, the net, their hands. Each of these smaller and larger pieces of the whole is itself a whole, a living center which helps to intensify the life of the other centers, and which is helped in its own life, too, by their intensity. It is this cooperation among the living centers which makes the group of men alive as a whole, and alive in its parts (in their hands, and eyes, and fingers, too.)

Some of this helping and mutually supporting life is visible in the centers which appear

within the system. In the diagram below the photo I have circled a handful of these centers: bits of space, corks on the nets, the distant palm trees in the sea, the space made by two men's arms in their adjacency. Altogether the life we feel in this photograph—and the life which was, undoubtedly, felt by them, at that moment of their existence—is caused by, in part created by, the interaction and mutual support among these many living centers, and by the fact that so many centers within the system are living ones.

13 / EXCITEMENT

I should like to complete my discussion of the way that centers help to create life from wholeness with a photograph of a single person in an acme of life: a girl throwing a ball, and her intense life. It is glowing, startling even, that this person, at that instant, had so much life in her, so much wonderful energy. I believe, even in this intense case, the life comes about because the centers have become vivid and intense at the moment captured. Her eyes, the position of her arm, the twist of her body—it is hard to show exactly how these are all centers; but as I have become used to looking at centers, judging their life, I see even this case as dependent on the way that individual centers, and the whole, in that person, at that moment, become intensely alive.

I have not given enough detailed information in this chapter to explain exactly how a human activity like throwing a ball could be seen as a cooperation of many living centers. But—hoping for the reader's indulgence—I do believe that this example, like the others, can be understood as a cooperation in which each center has its intense life, and in which the life of each center is helping to sustain, enliven, intensify, the intense life of some other center in the system. Her hands, eyes, the set of her arm, the center formed by the planting of her foot on the

ground—each of these centers, because of its intense life locally, cooperates with the whole, and creates the larger intense life which existed in her for that moment.

The wholeness—the structure of centers which exists—is animated or not according to the degree to which centers themselves have life, and this in turn depends on the degree to which

centers help each other, and on the density of centers. I believe that this conception of living structure can be extended even to cover the intensity of life in a single human being, where it accounts, to some degree, for the fire in the eyes of a young woman throwing a ball. In the diagram, we see how a handful of the living centers

in this girl are visible in the large and in the small.

The life of the component centers in a living structure is intimately connected with the fact that they are coherent, beautiful. What is surprising is that such a relatively simple scheme is capable of generating life.

APPENDIX

IMPORTANCE OF THE ACCURACY OF CENTERS IN A LIVING STRUCTURE

I should like to end with something that is by way of being a footnote — but a vitally important one. It concerns the minute subtlety and accuracy which is required, in order for centers to affect each other successfully.

Artists are aware, all too often, that a work can be made or broken by something that seems, to an outsider, a nearly trivial difference: a tiny spot of color, the shape of a curve. In buildings, too, the success of a room can depend on subtleties of placement where an inch this way or that makes all the difference, where a proportion changing by a few percent makes the difference between profound feeling and triviality. In natural living systems, too, a decimal point in a percentage of a chemical concentration can make the difference between life or death. In my experience this is not the exception, it is the rule.

Living structure is enormously susceptible to minor changes, and accuracy of detail is necessary for success. To strengthen the reader's understanding of this point, I should like to illustrate this effect, with an example I used earlier in the chapter (page 120): the ornament of a 15th century carpet border.²⁰

In 1988, I had an opportunity to study this carpet border, when working with students. I asked them, as accurately as possible, to draw the ornament. I wanted to show them how deeply the success of the ornament depended on the presence of all the centers it contains. This means, that in order to communicate the profound feeling of harmony which it has, it is necessary that more than a hundred centers and sub-centers are all shaped, within a hair's breadth, in order to have their own good shape, life, and positive quality. The students discovered, soon enough, that this was difficult to achieve, and that even when copying the ornament directly from a photograph, they were, more often than not, unable to recreate all the

living centers — and they found out that insofar as they failed to capture them, the ornament they reproduced had less feeling and less harmony.

As drawn by the weaver, the design has a beautiful, limpid, and almost deceptive simplicity. But if you start to draw it, you may become amazed: it is much harder to draw than it seems. The reason is, that its beautiful simplicity — in fact, its life — really does come from a highly subtle and complex structure of centers. You find that out when you try to draw it, because the structure of centers which contributes to this ornament is so subtle, and so complex, it is extremely hard to draw.

The centers which are present in the original design are shown in the diagram on page 121. If you look at that diagram, you can see that there are eighteen small drawings, each showing a center, with at least a hundred further and smaller centers appearing within these drawings. Some centers are small, some are almost as big as the whole pattern. To make the design work (i.e., to make it have the wonderful simple gracefulness of the original), all these centers must be present in the drawing and all must work as centers themselves.

When you try drawing it, a first attempt typically looks something like sketch 1, shown opposite. In this kind of sketch, which roughly catches the drawing of the quatrefoil, and not much else, there is very little feeling. You notice right away that your sketch does not have the same depth of feeling that the carpet ornament has, but you may not understand at once what has gone wrong.

In a second attempt, trying harder to get the details right, you may achieve something like sketch 2. This sketch contains more of the missing centers — but only about half of them. In this case, the sketch begins to have the subtlety and life of the original carpet, but the great

Sketch 1 is a highly inaccurate drawing of one part of the design. Most of the centers which should be there are missing from this drawing, or wrongly drawn: that is why it doesn't have much feeling. Sketch 2 is more accurate, but still wrong. In this drawing perhaps fifty percent of the centers are present, and the design is visible in something approaching its proper state: but the limpid and beautiful simplicity of the actual weaving is not present—because half the centers are still missing, or distorted, or too weak.

depth of life that is in the actual weaving is still missing. The reason is, the sketch is still missing half the centers which need to be there. For example, the rosette in sketch 2 does not have a nice diamond-shaped center in its middle, neither in the white nor in the black, as the real ornament does. There are no shaped centers in the white shape between the petals of the rosette, as there should be. At the top of the figure the fleurs-de-lys figure is distorted and almost invisible. The bottom lobe of the four petals does not form a nice center with its "stem" as it should do. And so on. Sketch 2 was made after the draftsman was aware of the centers, but he still did not see enough, or know how to make these centers properly.

This experiment shows how vital the centers are to the life of the whole. Perhaps for the first time, in trying to copy such a design, and in failing, we begin to see in real terms—terms that are actually experienced—how the life of the whole depends on the presence of the centers in a strong form, and on the way they help each other properly, and deeply.

That means it is not enough for the centers merely to be present in the drawing. To make the drawing work, each of these one hundred centers must be drawn in such a way that it is beautiful and has its own strength.

It is also instructive to find out how hard it is to draw all one hundred centers as strong, living centers even when you know what they are. The

reason is that when you draw you do not necessarily draw the centers as beautiful centers. Even at a late stage you may still not fully realize that the life of the pattern, the life of the rosette shape, the life of the fluers-de-lys, all come from the beauty of their subsidiary centers. You may find yourself trying to copy lines, curves, shapes—but do not concentrate sufficiently on copying centers because you do not understand that everything that is important and valuable about the pattern lies in the structure of its centers.

Also, drawing the centers so that all of them have life in them is geometrically and physically hard to do. Even after you have recognized how important the centers are, you will find that you cannot easily make all the centers work at the same time. You fix one, and another goes off. When you make that one, another becomes distorted. It takes enormous skill and concentration to draw the pattern so that all the centers at once have their full strength. To do it requires a mode of perception (unlike the one we are used to) in which every pencil stroke is creating centers, and more than one at a time. Suppose, for instance, that I make a dot to start my drawing. As I draw I have to be aware of half a dozen centers which this dot is part of; I must shape all six of them well, at the same time that I draw the dot. Then,

in the next instant, as I place the next dot, I may have to look at eight other centers, different ones, which are involved in that second dot, and which must be created by that dot.

To have the multiple parallel vision which is required to see and pay attention to all these centers at the same time while placing a single dot, requires blankness, flexibility of vision, and a relaxed and open state of mind. Above all, it requires the wide-open-eyes mode of perception which is described in appendix 3. It cannot be done without seeing the wholeness itself.

In conclusion then, we must be aware that a living structure comes to life only when the density of centers is present, and for it to be present, every center, at every scale (many of them large, but overlapping), must be shaped with the greatest care. It is this highly articulate and conscious structure, which must be—for an artist or an architect—the culmination of his art. Without this dense presence of living centers, life is unattainable.

Many of the centers that have to be protected, are centers in space; and it is often, above all, the positiveness of these centers in apparently unfocused space, which creates the life of a living structure. To accomplish this requires concentration at a level which is hardly ever taught in architecture schools today.[21]

THE KEY TO MAKING LIVING CENTERS

The reader may wonder how, exactly, one is to get a grip on the making of living centers. If they are as subtle as the last passage suggests, how, as a practical matter, can one hope to get them right—especially if making something new, in uncharted territory? The ways in which centers become living, and can be

built from other centers, in such a way to make them living, depends on a certain limited number of practical rules. These rules, described in the next chapter, control the ways that living centers can be made from other centers. As far as I have been able to determine, there are only fifteen of these rules.

NOTES

1. George Bernard Shaw's play, BACK TO METHUSELAH (London: Oxford University Press, 1947), contains a poetic evocation of this idea that I like very much, where Lilith says: "I am Lilith: I brought Life in to the whirlpool of force, and compelled my enemy, Matter, to obey a living soul. But in enslaving Life's enemy I made Life's master; for that is the end of all slavery; and now I shall see the slave set free and the enemy reconciled, the whirlpool become all life and no matter."

2. If any reader is not sure how this test can be performed, in chapters 8 and 9, I give various criteria which allow us to determine which of two centers has more life. In practice, this test is not hard to do, and by now I do it routinely in my work as an architect.

3. The use of centers as the fundamental building blocks of life or wholeness appears in an art-historical context in Rudolf Arnheim, THE POWER OF THE CENTER: A STUDY OF COMPOSITION IN THE VISUAL ARTS (Berkeley: University of California Press, 1982). It was also the foundation of Boscovich's theory of matter, presented approximately two hundred years ago. Boscovich had a conception of abstract point centers as the fundamental entities. Roger Joseph Boscovich, A THEORY OF NATURAL PHILOSOPHY (London, 1763; reprinted Cambridge, Mass.: MIT Press, 1966).

4. In mathematics it is common to have mathematical entities which are defined recursively, and such recursive definitions lead to well-defined and unproblematic mathematical theory. They arise most commonly when, for one reason or another, we have a system of functions, $f(n)$, and cannot define them in terms of other concepts, but do have a set of defining relations which exist among the $f(n)$ for different $n$. See, for instance, R. L. Goodstein, RECURSIVE NUMBER THEORY: A DEVELOPMENT OF RECURSIVE ARITHMETIC IN A LOGIC-FREE EQUATION CALCULUS (Amsterdam: North-Holland Publishing Company, 1957).

5. In the mechanistic world-view, a machine is built out of elements. We define the elements, and then assemble them to form some larger structure which gets its behavior from the interaction of the elements. However, wholeness does not come about in such a simple-minded way. It is my view that wholeness comes about precisely under those circumstances where centers are made, only, from other centers, and where more primitive elements do not exist.

We are used to a view where we try to explain one kind of entity by showing it to be constructed of other different kinds of entities. An organism is made of cells; an atom is made of electrons, and so on. But here we have a situation where we shall see that centers are so fundamental that they cannot be explained, or understood, as composites of any other more fundamental kinds of entities. Instead, centers are only made of other centers. This is the most fundamental concept. The nature of these centers can therefore be understood only reflexively, or recursively. This is the reason that wholeness looks so mysterious to those who are wedded to mechanistic thought.

6. In an interesting passage, Alan Watts seems to anticipate the idea of a field-like center: "Theoretically, many scientists know that the individual is not a skin-encapsulated ego but an organism-environment field. The organism itself is the point at which the field is focused, so that each individual is a unique expression of the behavior of the whole field, which is ultimately the universe itself. But to know this theoretically is not to feel it to be so." From Alan Watts, "The Individual as Man/World," reprinted in Paul Shepard and Daniel McKinley, THE SUBVERSIVE SCIENCE: ESSAYS TOWARDS AN ECOLOGY OF MAN (New York: Houghton Mifflin, 1969), 139-48.

7. In physics a field is a system of variables whose values vary in some systematic fashion throughout space. The simplest kind of field is a scalar field. This is a field in which there is a magnitude of a single one-dimensional variable associated with every point in space. An example of a scalar field is the distribution of some hormone (a specific chemical) in the human body. For this chemical, each geometric point in the body has a definite and different concentration. In this case the field is the overall spatial pattern of concentrations which allows the chemical to produce differential growth in different parts of the body, and thus to control the growth of beautiful and complex structures. A vector field is more complicated. A classical vector field is a spatial system which associates not only a magnitude, but a direction and magnitude, with every point in space. For example, the flow of water in a basin may be considered as a vector field. At every point the water is flowing in one particular direction, with some particular velocity. Both speed of flow and direction of flow vary from point to point. The pattern made by the varying velocities and directions constitutes the vector field.

Advanced physics contains many more complex fields. But none of them, unfortunately, have the character of the field I describe in this section.

8. This situation is mildly reminiscent of the bootstrap theory of particles, which was put forward in physics at one time by Geoffrey Chew. There, too, there were no ultimate entities, and every particle was to be defined in terms of other particles. Geoffrey Chew, LECTURES ON MODELLING THE BOOTSTRAP (Bombay: Tata Institute of Fundamental Research, 1970).

9. This topic, unresolved for the moment, is discussed more fully in appendix 4. In appendix 4, I have suggested some steps in the mathematical effort to define such a field. It is unlike other fields which have so far been defined in mathematics. Only my sense that it ought,

in principle, to be possible to define a new kind of field that embodies these characteristics, is what makes me call it a field, and a field effect. In the field of centers, what varies throughout space is the overall orientation produced by the other centers. The great difficulty of making this field concept precise is discussed in the appendix. At present, mathematical theories known to me do not include a model which has the necessary behavior. Precise treatment of the field of centers concept, or the idea of a center as a field, must await formulation of a new type of mathematical structure that fits the situation.

10. Further discussion of local symmetries as approximations to centers can be found in chapter 5, and in appendices 2 and 6.

11. I apologize for the roundabout presentation, here referring to something which appears in chapter 5, later in the book. In any case it seems the best way to present the argument. The fifteen properties are fully defined and discussed in chapter 5.

12. The idea that every center has its life makes the "life" of the centers the ultimate primitive of this theory. This is perhaps comparable to Robert Pirsig's idea that Quality, not Substance, is the ultimate primitive. As Pirsig puts it, "Quality is supposed to be just a vague fringe word that tells what we think about objects. . . . The idea that quality can create objects seems very wrong . . . but the idea that values create objects gets less and less weird as you get used to it." Robert M. Pirsig, LILA (New York: Morrow, 1991), 98, and 97-106, and ZEN AND THE ART OF MOTORCYCLE MAINTENANCE: AN INQUIRY INTO VALUES (New York: William Morrow, 1974). I am saying something similar about that which animates the living centers.

13. The idea that life might come about as a recursion among undefined entities is touched on by Douglas Hofstadter, GOEDEL, ESCHER, BACH: AN ETERNAL GOLDEN BRAID (New York: Random House, 1979). It was also discussed extensively through the idea of holons, by Arthur Koestler, in JANUS: A SUMMING UP (London: Hutchinson, 1978).

14. This fragment stood before me for years, in my study, while I was working. I bought it from an art-dealer in Chicago, who told me that it was stolen from the Alhambra a hundred years ago, long before people started taking preservation seriously.

15. If you have trouble doing this, please read chapters 8 and 9, and use the techniques described there.

16. The use of the word "bootstrap" here again refers to the phrase "lift yourself by your own bootstraps," commonly applied to those theories of particle physics in which there are no elementary particles, but each particle is "made" of all the others. See Chew, LECTURES ON MODELLING THE BOOTSTRAP.

17. However, to make this work, we do need a conception of a kind of space in which these things can happen. In the end we shall be able to penetrate this apparent circularity only by modifying our idea of space to a form of space which explicitly includes provision for this feature. See appendix 4, and the last pages of chapter 11. I believe this recursive and apparently cyclical set of relationships will then be seen as the key to the phenomenon of life.

18. Bill Mollison, PERMACULTURE (Washington, D.C.: Island Press, 1990).

19. Please see, for example, the discussion throughout chapters 10 and 11, where I discuss, in some detail, the unity of function and geometry.

20. This beautiful design was drawn at the end of the 14th or beginning of the 15th century, and now remains with us in only two carpet fragments and one painting. The ensuing discussion follows Christopher Alexander, A FORESHADOWING OF TWENTY-FIRST CENTURY ART (New York: Oxford University Press, 1993), 176-79.

21. Please bear in mind that my view is that all life — not only the life of abstract patterns or works of art — can be characterized in this way. This means that the same intense multiplicity of structure, the same densely-packed pattern of coherent, positive centers that I have illustrated here, is to be seen in living structures in biology, through nature, in natural ecological systems.

I remember being astonished, a few years ago, by seeing a Magnetic Resonance Imaging (MRI) cross section of a human neck. What amazed me was the compactness of the tissues, the way they all fitted together. I had always had (previously) a rather naive and totally inaccurate view of human body as a kind of bag, loosely filled with organs, tissues, nerves, and so on. Old-fashioned illustrator's drawings of the body tended to reinforce this view. But seeing the MRI cross-section of a human neck makes it clear that it is, internally, a wondrous structure of carefully constructed coherent form, interlocking, overlapping, and richly woven, so complex and beautiful geometrically that every space, every nook and cranny has not one, but multiple functions, and participates in the form of several, multiple, coherent, geometric structures.

In this regard the human body has the same overall character as the ornament I have discussed — and so must any living structure of any kind. That, at least, is my belief.

CHAPTER FIVE: FIFTEEN FUNDAMENTAL PROPERTIES

1 / INTRODUCTION

I have introduced the idea of life as something which may occur in any spatial system, and suggested that the degree of life which appears in a thing depends on the life of its component centers and their density. Thus, broadly, we have a theoretical scheme in which the life of a thing, or building, or system, depends on the extent to which the centers in this thing cohere and help each other. What follows in this chapter is an analysis of the different ways in which this can occur.

About twenty years ago, I began to notice that objects and buildings which have life all have certain identifiable structural characteristics. The same geometric features keep showing up in them, again and again. Initially I began writing these characteristics down informally, and I began to "keep watch" on them.

What I did was straightforward and empirical. I simply looked at thousands and thousands of examples, comparing those which had more life with those that had less life. Whenever I looked at two examples, I could determine which one had greater "life" or greater wholeness, by asking which of them generated a greater wholeness in me. Thus, I did not impose on myself the modesty of judgment typical in a pluralistic society. I did not worry about "my" values compared with someone else's values. I simply identified those examples which had the greater wholeness, judging this by the degree of wholeness they induced in me, and assuming, with as much confidence as I felt to be real and reliable, that what I measured here would also be shared with others.

I asked myself this question: Can we find any structural features which tend to be present in the examples which have more life, and tend to be missing in the ones which have less life? In other words, can we find any recurrent geometrical structural features whose presence in things correlates with their degree of life? To

find this out, it is necessary to make thousands and thousands of comparisons, to ask oneself constantly whether any features can be identified which correlate with the degree of wholeness which things have. This is what I did. For twenty years, I spent two or three hours a day looking at pairs of things — buildings, tiles, stones, windows, carpets, figures, carvings of flowers, paths, seats, furniture, streets, paintings, fountains, doorways, arches, friezes — comparing them, and asking myself: Which one has more life? And then asking: What are the common features of the examples that have most life?

I managed to identify fifteen structural features which appear again and again in things which do have life.¹ These are: I. LEVELS OF SCALE, 2. STRONG CENTERS, 3. BOUNDARIES, 4. ALTERNATING REPETITION, 5. POSITIVE SPACE, 6. GOOD SHAPE, 7. LOCAL SYMMETRIES, 8. DEEP INTERLOCK AND AMBIGUITY, 9. CONTRAST, 10. GRADIENTS, 11. ROUGHNESS, 12. ECHOES, 13. THE VOID, 14. SIMPLICITY AND INNER CALM, 15. NOT-SEPARATENESS.

At first, I observed these features without understanding what they were. I simply recorded them. And, indeed, up until about 1985, I did not really understand what these fifteen properties were. That is, I understood each of them by itself as something which was present, often or very often, in a living system—to such an extent that one might almost say that each one was a predictor of whether a thing would have life or not—but during that first decade of study I did not understand why these fifteen properties had this effect. I did not even understand the key role which centers play, the key role of the wholeness. In the list of these fifteen properties as it first appeared, in unpublished manuscripts from 1975 to 1985, one of the fifteen was CENTERS, but I did not know then that this particular item had any kind of logical priority over the others. I simply knew that the presence of strong centers,

I44

just like the presence of the other fourteen properties, made a system more likely to have life.

During those many years of observation, I often asked myself what these fifteen properties signified, what they are, what they do. And finally, I came to understand that all of them are, in effect, just the fifteen ways in which centers can help each other come to life. I came to understand that they work, they make things have life, because they are the ways in which centers can help each other in space.

As a writer I now have two options open to me. I could present these fifteen properties as they first appeared in my mind—as nearly raw observations about things which help buildings and objects have their own life, without reference to their dependency on centers. In this form of explanation, I would describe them as I first saw them, fifteen isolated, independent properties, with no special rhyme or reason to them, just as end-products of observation. I could then explain, at the end, how the fifteen of them are just those ways in which centers are able to help each other—indeed the only ways—thus explaining why they exist and have such a powerful effect.

Or, I could start with a different kind of explanation, showing from the very beginning that these are indeed the fifteen ways in which

centers help each other, emphasizing their relationship to centers, and showing how they do it. But if I did this, the raw force and empirical force of the observations I originally made would be lost to the reader. There might be something too polished, almost contrived, about my presentation, and you would miss the empirical excitement of the process of observation and perhaps, therefore, be less able to see for yourself, by making your own observations in the world, that these fifteen properties, as features of life, really are true, necessary, and empirically verifiable. This would be a great shame. What I shall try to do, therefore, is to go between these two methods of presentation. I should like the reader to feel the raw excitement I felt, when I first began to notice these fifteen properties, and tried to define them, to make them precise.

But I should also like the reader to understand how these fifteen properties fit together with the theory I have presented in chapters 3 and 4—how indeed they form one of the underpinnings of that theory—something that I did not understand originally, and something that was in fact not available to me as an idea during the first ten years of my observations. My task was a simple scientific one: to find out what I could about the structural correlates of life by making observations and distilling them.

2.1 / LEVELS OF SCALE

The first thing I noticed, when I began to study objects which have life, was that they all contain different scales. In my new language, I would now say that the centers these objects are made of tend to have a beautiful range of sizes, and that these sizes exist at a series of well-marked levels, with definite jumps between them. In short, there are big centers, middle-sized centers, small centers, and very small centers. In the language I used at that time, I would simply have said that I noticed a great variety of well-formed

wholes of many different sizes and that this was often the first thing one noticed about those things which have great life in them.

This observation may seem obvious—almost tautological. But it is not obvious at all. As we shall see, many things which have been made in our period of history do not have this feature. On pages 146-7 is a pair of examples, one with good levels of scale and one with poor levels of scale. The Albers painting has very poor levels of scale. There are subtle differences of size

among its elements, but there are no noticeable levels. As a result, the painting seems dead, lacks depth. The Matisse drawing, on the other hand, has a remarkable range of scales. There is the young woman's body as a center; the centers formed by the large open area on her back; the intermediate centers like her head, the hat, the brim; smaller centers like the flowers; and the very small centers like the petals in the flowers and the details of lace and buttons. The range of scales forms a continuum which ties the drawing together and makes it whole. This is what gives the drawing its life.

If you compare any two things, one with more life and one with less, it is very likely that the one with more life will have better levels of scale in it. The idea is far more subtle than it seems. To understand its subtlety, consider the following pair of doors. Both doors have parts of different sizes in them: panels, jamb, moldings, handle, and so on. But the old Irish door on the right has a variety of sizes which is more dramatically differentiated, more "extended"

along the range of scale than the door on the left. It has three sizes of panels; it has a gradation of scale from the bottom to the top. It has the jambs that are smaller than the panels, and the stiles are smaller than the jambs. It has a handle which has LEVELS OF SCALE within itself in the lock and in the finger plate.

Now let us consider the left-hand door, with eighteen equal panels. Why does this fail to have the levels of scale property as much as the right-hand door? In the right-hand door, we experience the levels more deeply for two reasons. First, there actually are more levels: because the panels are more finely differentiated, there are centers formed at intermediate scales, formed by the top panel and middle panel together, for example — something that doesn't happen in the other door. But what is really missing is the degree to which the centers help each other. In the right-hand door this helping is made to occur by the levels of scale. The actual life of each center comes about because it is enlivened by the size and position of the next larger center which lies near it, and by the size and position of the next smaller center which lies near it.

In the left-hand door the detail is there—but the detail isn't doing anything to create life in the larger centers, and is therefore almost meaningless. Superficially, the left-hand door has many panels, hence many levels of scale. But although there are indeed many panels forming an impression of scale in the door, these panels are cut in on a machine jig, automatically, as they often are in a door trying to be like an old-fashioned door. So, the centers in the panels have no real life. And this comes about because the centers are not really made to help each other. The door-maker, I can say quite confidently, was not trying to make this happen. Probably it was made in a factory, without much attention to the individual door. So, the levels of scale are rather superficial and empty.

Thus the property of having levels of scale is not a mechanical thing, which merely requires a wide range of different sizes. It arises properly only when each center gives life to the next one.

It is also extremely important that to have levels of scale within a structure, the jumps between different scales must not be too great. For example, if we look at the concrete wall in the picture below, we shall see the wall itself as a center, and we also see small individual centers (bolts or bolt holes) still visible from the formwork. Naively one might therefore say, "The concrete marked by the small bolts has levels of scale." But according to my definition of this property, it does not. These two systems of centers (the whole wall and the small bolts) are too far apart in scale to be coherent with each other. Each panel of the wall itself is perhaps 36 inches by 72 inches. The individual bolts are perhaps an inch across. The area of the whole wall segment is

thus about 2,000 square inches while the area of one bolt is less than 1 square inch. The jump in scale is 2000 to 1—far too great to form levels of scale—too great to form a nice chain of levels, or a nice step in levels.

When we introduce a single level at a jump of about 20:1 we get something like the modern—and undifferentiated—vase shown at the left. Here, still, the jump in scale of 20 to 1, between neck and body, is too great. It doesn't do anything to bring life to the structure.

Much better, and beautifully proportioned, are the levels of scale in the pottery horse. It has simple, strongly executed levels of scale. The body is about twice the size of the head; the head about twice the size of the legs; the legs about twice the size of the feet and hooves. These details, not quite real when compared with the levels in a living horse, are dramatically and beautifully judged, just so that each level really helps the level next to it. The pottery horse has its life as a result.

In the vase below, the scale-jumps are more beautiful still. They are magnificently gauged. The body of the vase is perhaps three times the size of the neck: the neck falls in two parts, one three times the size of the other; and the upper part of this "neck-band" is perhaps three times the size of the ornaments chiselled into the top neck band. For some reason, especially in the impact of the body of the vase, the levels of scale have a nearly chilling power to create real life.

If the jumps in scale are heavy, deliberate, and somewhat evenly spaced through the levels of scale, a thing will often have this powerful life. For instance, in the good vase the jumps are roughly 3:1 and 3:1 and 3:1 and 3:1 again, step by step as we go down in scale. In this case, the life which is attained in the object is very great indeed. See also, for instance, the exterior of the Meshed mosque shown on the facing page.

Throughout these examples we see that a center becomes most intense in its life when other centers near it have a definite size relation to it at a scale which is perhaps half its size, or twice its size—but not enormously bigger, or

enormously smaller. To intensify a given center, we need to make another center perhaps half or quarter the size of the first. If the smaller one is less than one-tenth of the larger one it is less likely to help it in its intensity.

Let us understand clearly, then, what this levels of scale is actually doing in an object. It provides a way in which one center can be helped in its intensity by other smaller centers. If I try to make a certain window a strong center, then I can intensify this center by making a second smaller center to support the first, at the sill, or at the jamb, or in the wall next to the window. This second center will tend to be most helpful in intensifying the first one (the window itself) if it is not too different in its size. For instance, a window can be intensified by a windowsill, but it is unlikely to be intensified by a nail. And, often, a big sill will do it better than a small sill. Thus, the centers need a rather well-ordered range of sizes and scales in order to help each other most practically.

In the tilework at Meshed, we see this principle carried from the giant tower-like structures through many intermediate levels, all the way down to the tiles themselves. There are distinct wholes, or centers, visible at every level in between the two.

The same is true of the sparse but magnificent high porch near Isfahan on the next page, where the rooms, members, and scales help our feelings by supporting practical life profoundly. In the more miserable structure of Le Corbusier's Marseilles apartments (shown at right), there are merely a few distinct sizes of things visible, as in any design, but no way in which each level has its centers, and in which one clearly feels how each enlarges and enlivens the smaller ones and larger ones. The different-sized members are merely different in size. But in the good examples, like the porch on the next page, the levels of scale create a field effect which creates centers: it is not only true that the small centers intensify the large ones, but the large centers also intensify the small ones. The property creates life by helping centers to intensify each other.

FUNCTIONAL NOTES

Throughout this chapter references to a PATTERN LANGUAGE (New York: Oxford University Press, 1977) will be given in shorthand as APL, followed by the name of the pattern and a page number.

Levels of scale are necessary to many practical examples from the sphere of building and a great many patterns in APL deal with this topic. Construction members, especially in their connection to one another, are helped and complemented by small pieces of trim which set a hierarchy of levels in the finish work, cover cracks, and make the finishing more practical (HALF INCH TRIM, p. 1112). A window works best, emotionally, when it is divided into smaller windows. The subdivision of panes helps the way the window creates a view. The glazing bars also add strength, and make it easier to replace broken glass without waste (SMALL PANES, p. 1108).

Larger examples of levels of scale are equally significant. Consider the structure of regions, communities, and neighborhoods. INDEPENDENT REGIONS, COMMUNITY OF 7000, IDENTIFIABLE NEIGHBORHOOD, and HIERARCHY OF OPEN SPACE (pp. 10, 70, 80, 557) all show that distinct and definite levels of scale in the large structure of the city will help maintenance of human community.

Or consider the variety of room sizes in a building. Several patterns in APL deal with this topic. The patterns to do with the necessary variety of different activities in a building, and the resulting variety of size of different rooms. Buildings whose rooms are all the same size are often rather stale. But in a house with a large room, and smaller rooms, the social atmosphere and the range of possibilities for life which the building provides are intensified. Even a tiny house in which there is one dramatically large room, two small rooms, and two tiny alcoves, will work very much better than one in which there are four equal-sized small rooms (ALCOVES, BED ALCOVE, CEILING HEIGHT VARIETY, pp. 828, 868, 876).

In all these examples the smaller spaces somehow bolster the life of the larger spaces; and the larger ones bolster the life of the smaller ones. There is more cooperation in the life of the different rooms when there are extremes of size variation, than when sizes are homogeneous. Thus, in these examples, levels of scale among functional centers affect the practical behavior of the building, and make it more capable of supporting life.

2.2 / STRONG CENTERS

The next property—the frequent appearance of STRONG CENTERS in living structures—appeared in my list of properties about 1975, long before I recognized the more fundamental and more general role of centers as the key elements of all wholeness. When I first noticed it, it was simply as one characteristic of those wholes I observed in living structures.

It may seem strange that I now choose to leave it on the list as one of fifteen properties, when I know that centers play a much more fundamental role as basic elements. Nevertheless, I leave it in the list, because it is one thing to emphasize the presence of centers as elements of the wholeness—as I have done in chapters 3 and 4—and quite another to concentrate on the strength of these centers as a feature all the centers have in living structures—which I do here. What follows is essential, and not covered in the earlier discussions.

I began to notice that, next to the property of LEVELS OF SCALE, possibly the most important feature of a thing which is alive is that we find that the various wholes which exist at different levels appear not merely as centers or “wholes” or “blobs,” but actually as strong centers.

Contrast two buildings: the mosque of Kairouan and the house by Bruce Goff above. As we look at the mosque, we see many mutually reinforcing centers. The great courtyard, the large dome, the smaller dome, the individual battlements, the steps, the entrance, the individual arches, even the segments on the roof. In contrast, there are virtually no strong centers at all to be seen in the Goff house. Some people might call the house organic. But it lacks the cumulative power of strong centers which I am talking about. Whether you think that the wholes it is made of are wholesome or not, you can hardly claim that they form strong centers. Its elements are amorphous in a definite and intentional fashion, which prevents them from being strong centers.

To some extent, the difference between the two buildings is caused by a difference in symmetries. In the mosque the various centers which exist are locally symmetrical. In the house almost none of the parts are locally symmetrical. But the fact that there are strong centers in the one building, and not in the other, depends on more than symmetry. In the mosque each center exists as a field-like effect, which extends beyond the local symmetry of the individual parts. For example, the power of the dome in Kairouan is caused by the progressive sequence of three domes, each one higher than the other, leading up to the main dome as a pinnacle. The entire structure builds up to the main dome. The fact that we perceive this dome as a center is caused not just by the shape of the dome, but by the location and geometric role which this dome has in the building complex as a whole.

By contrast, in the Goff house, there is none of this progressive quality. The individual parts are not intensified by their position in the whole, except perhaps for the one or two small leaf-like roofs over the central tower, the other elements stand in isolation, and do not create any feeling of centeredness in one another.

To understand this quality more dramatically, let us look at an Anatolian carpet fragment from the 18th century. It has the feature of centeredness to a striking and extraordinary degree. Almost every good carpet has some strong center, not necessarily a geometric center, but a center of attention, a center of focus. If the center is merely a something in the middle, which disappears when you cover it, it has very little power. In order to work as a strong center, there is usually the feeling that the entire carpet is orga-

nized in layers to support and surround this middle, so that one approaches this middle, the eye rests on it, one keeps coming back to it, going away from it, coming back to it. In short, the entire design sets up a vector field so that every point has the property that from that point the center is in a certain direction: one direction is going to the center, and another is going out away from it. As a result, the whole visual field is oriented towards the center, and the field feels centered. Even when you put your hand over the

middle, you can feel the center just by looking at the vectors set up by the layers all around it. In this great Anatolian carpet the red figures progressively take the eye to the middle; again and again, each part takes the eye to another part, which moves towards the middle. The cross shapes at the end seem to point out, yet oddly create a field effect towards the middle. The diagonals in the border seem unconnected, and yet powerfully send the eye again on a diagonal path, which ultimately moves towards the middle.

In a building, creation of this kind of centeredness can be considerably more subtle. The imperial inner city of Beijing has a centered quality. It is a layered system of nested domains which lead, one by one, to the inner city, and then to the inner sanctum of the inner city. The hierarchy of layers creates the deep feeling and intensity of the center: the deep center arises at the heart of the inner city, because of the field effect generated by the nesting. We pass through a series of zones of increasing intensity as we go into the

building: the gradient of increasing intensity creates a center in the middle.

The Potala courtyard shown opposite has a similar structure in three dimensions. Arcade, columns, capitals, detail—each one contributes to the overall field effect, which makes each of these centers, large and small, so powerful. Look at the way the column capital creates a field effect which makes the column bay more intense, at the way the bay, becoming intense as a center, then creates a field effect in the courtyard where the photographer stood, making this courtyard a stronger field-like center, too.

In contemporary buildings, it is often hard to create this hierarchy of centers, perhaps above all because—in practical terms—we don't know what to put at the center. A typical house of a modern family. What is the center? Above I show a typical house with a number of rooms and little clarity. It reflects a situation where people wander in and out, relationships change, little is stable. The plan itself lacks a center, even in the physical organization, which perhaps reflects a lack of center in the modern idea of the family. But if we want to know how to correct the problem, we find ourselves asking, "What function could there be at the center that is important enough to make the building have a series of levels in this fashion? The kitchen? the movies or CDs of the day? the living room?" These functions, though important, are too neutral emotionally to be able to carry a powerful geometrical center. What once were powerful centers—the fire, the marriage bed, the table—no longer have this power, because individually

and as families we are not centered in ourselves. The emotional confusion of the present-day family reveals itself in the lack of power in these centers of the house.

But when a house is organized with clearer centers—with a center that exists in the plan as a focusing field of energy, focusing the house towards a place—it becomes immediately more potent, even in its ability to harness unknown and undeveloped tendencies of centering in the life people live there together.

To clarify the idea of a strong center look at the example by Frank Lloyd Wright, above, which allows us to study the field effect which creates a center. The field effect and the power of "the" center are created by the sequence of other nearby centers leading up to it. For instance, a long religious building with a series of bays leading to one end will mean more if the bays become more and more intense, leading to a climax, than if they are all equal. In general, there is some kind of principal structure, and other structures are subsidiary to it. There is one largest structure guiding the whole.

Sometimes this weight, or centrality, can be created by apparently small details. For example, the lamp hanging in the prayer arch (mihrab) of a prayer carpet has a certain very definite function: to hold the eye, to make a center. But it is not enough for the lamp to be a dot. It needs to be a "structure" which forms centers in itself, perhaps, as a minimum, a large dot, with three smaller dots below it. It can even be an upside-down jug, any design with enough structure to establish a strong field effect.

In the complex and sophisticated carpet example with five niches, from the 15th century, the lamps play an enormous role in making the niches into strong centers. Although the niche-centers are effectively created by the lamps, it is not the lamp itself which is the center. The lamp merely serves to orient the space, and to set up a field effect in the larger space. The center which is then created is a centered, oriented zone, five or ten times bigger than the lamp alone: and it is this which creates the deep feeling in this carpet.

The lamp is just one of many structures which create a progressive sense of movement towards the core of each niche. It is the overall, combined effect of all these different centers working together which creates the strong center. The reason why a single dot would do less than a "lamp" is that the lamp itself is a progression of centers, not just a single center—and this

progression of centers, in this one place, will do more to organize the field than a single spot could do.

As in this example, every strong center is made of many other strong centers, a multiplicity of centers. Like levels of scale, the concept of a strong center is recursive; it does not refer to some one grand center, but to the fact that at a great variety of scales, in a thing which is alive, we can feel the presence of a center, and that it is this multiplicity of different centers, at different levels, which engages us.

In many cases there is nevertheless one principal center, the center of the whole composition — the resting place, the middle, the most important place. In other cases which are equally breathtaking, there is no one center, but an undulating series of minor centers, as in the deer on the plate shown on the facing page. But even in cases like these we see, at various points, things which we can identify as "centers," forming and making other centers powerful and strong.

The tip of each roof in the trulli at Alberobello is a strong center which is formed, not merely by the little knob, but by the way the whole roof form is focused towards the tip, the way the tip is painted white, and the way this then culminates as a core of a center that is formed. The forged iron handle gets its strength as a center from the two plates, forged top and bottom, which are then screwed to the door. The

deer on the Turkish plate becomes a strong center because of the way it stands out from the repeated roundel elements, and from the border, which all focus their attention on the deer. In the Piazza San Marco the front of St. Mark's, the irregular shape, all focus towards that one spot where the campanile stands: it is carefully focused to create this field effect.

FUNCTIONAL NOTES

Many cases discussed in APL show how spaces become more useful, or more deeply felt, when they are made strong centers (MAIN BUILDING, p. 485). For example, it is necessary to provide a fireplace, or something equivalent, as the nucleus of a main living room (THE FIRE, p. 838). It is necessary to organize the center of the house as a point to which all other paths are tangent (COMMON AREAS AT THE HEART, p. 618). One should see the sunshine as the kernel of a south-facing area just outside a house (SOUTH FACING OUTDOORS and SUNNY PLACE, pp. 513 and 757). It is necessary to see the seating area of a room as a protected kernel of activity, with its own hull, and its own edges protected from circulation (CORNER DOORS, p. 904).

Strong centers also play a key role by creating necessary focal points in the city, at the urban scale (see, for instance, MAGIC OF THE CITY, p. 58, SMALL PUBLIC SQUARES, p. 310, HIGH PLACES, p. 315, SOMETHING ROUGHLY IN THE MIDDLE, p. 606, TREE PLACES, p. 797).

And again, strong centers also play a fundamental role in the construction of graded sequences which protect privacy and deeper feeling in a building. Rooms which are public and easy to get to, gradually leading to rooms which are more remote, and then leading to others still more remote. The field-like quality of each center comes from the gradient as a whole (APL, INTIMACY GRADIENT, p. 610). Sometimes, even the most remote rooms are public, not necessarily private—but they have a beautiful stillness about them if they lie at the end of such a sequence.

Finally an example from construction: when we install a window, we locate the window as a center first (its rough frame), then set the finished sash in the rough frame. As we do it, the fine-tuning of the verticals, the sill, trims, and fine trims we place, all work together to make its edges become centers; and in so doing we make the window as a whole a center. The strong center arises from the practical problem of setting a precise square sash into a rough opening, and making it as neat as possible.

2.3 / BOUNDARIES

Early in my studies I noticed that living centers are often—nearly always—formed and strengthened by BOUNDARIES. You may see this strengthening in traditional architecture, and the lack of it in many contemporary buildings. Compare the following: The Norwegian storehouse is replete with boundaries at every scale. The other building on the opposite page—a condominium from around 1950—has virtually no boundaries at any scale.

The purpose of the boundary which surrounds a center is two-fold. First, it focuses attention on the center and thus helps to produce the center. It does this by forming the field of force which creates and intensifies the center which is bounded. Second, it unites the center

which is being bounded with the world beyond the boundary. For this to happen, the boundary must at the same time be distinct from the center being bounded, must keep this center distinct and separate from the world beyond it, and yet also have the capacity of uniting that center with the world beyond the boundary. Then the boundary both unites and separates. In both ways, the center that is bounded becomes more intense.

Boundaries do the complex work of surrounding, enclosing, separating, and connecting in various different geometric ways, but one vital feature is necessary in order to make the boundary work in any of these ways: the boundary needs to be of the same order of magnitude as the center which is being bounded. If the boundary is very much smaller than the thing being bounded, it can't do much to hold in or form the center. A two-inch border cannot hold a three-foot field. In a room, the boundary between floor and wall needs more than a six-inch molding—a wainscoting, 30 inches high, is more in scale

with both. An effective boundary for the river Seine consists of roads, walls, paths, quays, trees, something almost as massive as the river itself. In general it is necessary to think of boundaries as very large.

When taken seriously this rule has a very big effect on the way things are organized. For instance, the lips as the boundary of the mouth are similar in size to the mouth; an arcade as the boundary of a building is on the same order of size as the building; a truly generous window frame with deep reveals as the boundary of a window is of the size of the window itself; the marsh as boundary of the lake; the capital and base as boundary of the column. In all these cases the boundary is very large compared with the thing it is bounding—often surprisingly large.

On page 161 I show a simple center—a door—showing the effect of its boundary. The door as a center (Figure A) is intensified by placing a beautiful frame of centers around that door (Figure C). The smaller centers in the boundary

are also intensified, reciprocally, by the larger center which they surround. For example, suppose we look at the door frame without the door (Figure B). The centers of the frame are nice, already well formed and intense. Now, when we put in the door (Figure C), the centers in the outer boundary become more intense. The effect works both ways. The life of almost every center is caused by the fact that the center itself, and its subsidiary centers, too, all have strongly marked boundaries.

Having established the importance of size in a boundary, the next thing that is needed to establish the interlock and connection, coupled with separation, is that the boundary itself is also formed of centers. For instance, in the manuscript border on the next page, the boundary is formed of large centers, sometimes almost as large as the field, but made in such a way that they unite the thing bounded with the world beyond. They achieve this in various rather concrete geometric ways. Essentially they form centers, or systems of alternating centers, which look both ways: they face in and they face out; they create connections to the inside of the boundary, and connections to the outside, by establishing new centers that span the two. Some work by pure interlock (e.g., border of reversed arrows). Sometimes the border has a motif like a running vine, or alternation, which first relates to one side, then the other, creating ambiguity. At other times, the border is simply made of large square tiles, each one containing flowers: it has no special interlock but a feeling of similarity with what is on either side in terms of shape and color.

The boundary rule does not apply only to two-dimensional areas. Even a one-dimensional thing may be bounded by one-dimensional zones at its ends: for instance, the wooden ridge-beam of the Ise shrine is bounded by the brass cap that protects the end. A two-dimensional surface within a room may be bounded by other two-dimensional zones in space, for example, the wall of a room can be bounded at top and bottom perhaps by a wainscot or a baseboard at the bottom, and by a beam or zone of plaster at the top.

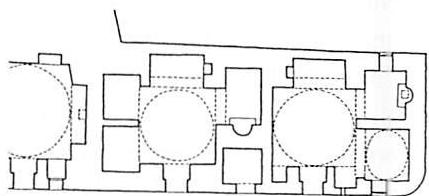
The rule also applies to volumes. A three-dimensional volume may be bounded by a smaller volume around its edge. For example, a building or a court can be bounded by an arcade, a room by a series of deep alcoves, the volume of the Seine in Paris by the waterfront quays along its edge and their magnificent trees.

There is a further point. Taken by itself, the boundary rule seems simple. But the rule does not merely refer to the outer boundary of the thing. If we apply the rule repeatedly, it says that every part, at every level, has a boundary which is a thing in its own right. This includes the boundaries themselves. They too have boundaries, each of which is a thing in its own right. What seems like one rule, then, is a pervasive structural feature of enormous depth, which is

in effect applied dozens or hundreds of times, at different scales throughout the thing.

And this makes it clear not only how immense a rule it is, but also how it is possible for a thing to follow this rule and still lack an outer boundary around the whole, because that outer boundary (present or not) is merely one of ninety-nine other boundaries which do exist within the whole, at different scales. So this rule by no means merely says that any center which has life, like a building or a town, must have a boundary. The limited idea of a main boundary by itself completely fails to convey the shimmering sense that is created when a thing has boundaries within boundaries, which are boundaries of boundaries, and that all together permeate its structure.

FUNCTIONAL NOTES

Here are some examples of the functional and practical needs for the effects of boundaries described in APL: a neighborhood needs a strong boundary around it (SUBCULTURE BOUNDARY, NEIGHBORHOOD BOUNDARY, pp. 75, 86). We need thickening of windows and doors around openings, to stiffen the membrane of the wall (FRAMES AS STIFFENED EDGES, p. 1059). At the scale of rooms, many rooms become most beautiful and useful when they are surrounded by window-seats, or alcoves, or thick walls, with cabinets and closets in them (ALCOVES, WINDOW PLACE, THICK WALLS, CLOSETS BETWEEN ROOMS, pp. 828, 833, 908, 913). A building itself is often made most comfortable in its relation to the outdoor spaces, if there are galleries, arcades, and terraces between the two (GALLERY SURROUND, ARCADES, OUTDOOR ROOM, pp. 777, 580, 764). NECKLACE OF COMMUNITY PROJECTS (p. 242) puts small public services around a major public building, to intensify the heart of a community.

All these patterns embody boundaries: but the boundaries work in different ways. Some, like alcoves, provide places where a small space intensifies the activities in a larger space by providing "thicker" boundaries. Some isolate sound: closets form acoustic boundaries between rooms. Sometimes the centers in the boundary focus life on the larger bounded center: this happens in arcades and galleries which form a boundary layer between inside and outside, and in the window-seats and thick walls around a room.

In all cases, the boundaries help one set of spaces to insulate and reinforce the functions of others by creating zones of separation and zones of mixing. The key point is that when the functions of the centers that form the boundaries are correctly chosen, this allows the smaller centers forming the boundary zones to intensify the functioning of the major centers being bounded.

2.4 / ALTERNATING REPETITION

One of the ways that centers help each other most effectively is by their repetition. Centers intensify other centers by repeating. The rhythm of the repeating center, slowly, like the beat of a drum, intensifies the field effect. But this drumbeat, when it intensifies the field effect, is not just simple repetition.

It is a fact about the world that things repeat. Most things are made from repetition at some level: repetition of atoms, crystals, molecules, waves, cells, volumes, roofs, trusses, windows, bricks, columns, tiles, entrances, and so on. But the repetition which occurs in things which have life is a very special kind of repetition.

tion. It is a kind where the rhythm of the centers that repeat is underlined, and intensified, by an alternating rhythm interlocked with the first and where a second system of centers also repeats, in parallel. The second system of centers then intensifies the first system, by providing a kind of counterpoint, or opposing beat.

To see it, let us start with some general examples of satisfying repetition. Consider the beautiful repetition of tiles on a roof, waves in the ocean, cells in the body, the scales of a fish, the blades of grass, the bricks in a wall, the hairs on a head.

In all these cases, the life itself seems to come largely from the repetition. We often see this in drawings in which we give life to the drawing by the simple repetition of a certain kind of pencil stroke. We often see it in buildings, where certain simple, distinguishable elements are repeated over and over again. The repetition, by itself, already begins to create a satisfying harmony. Somehow the sense of order in a thing comes from the fact that elements are repeated over and over and over again. And often the calmest life arises when a thing, like a basket, is made entirely out of one kind of smaller element, repeating.

Of course, in many cases where a structure gets intense life from repetition the repetition tends to be inexact; it is then the subtle variation which comes with the repetition that is satisfying and life-giving. This happens because the elements are not identical, but modified, each according to its position in the whole, creating a subtle variation in the repetition.

But there is a deeper aspect of the repetition, more vital than its variation. This concerns the fundamental character of the repetition and the way that elements are repeated: there is profound and satisfying repetition of living centers, and there is banal repetition of elements.

A crucial comparison which should make this idea clear is presented on the facing page. One example shows a subtle and delicate embroidery from a Greek island. The entire surface becomes whole, from the flickering alternation of the shapes and spaces, all repeating, all alternating. Both primary and secondary centers in the repetition are alive; that is what causes the alternation, and what engages the eye continuously. The glass jug on page 167, with its beautifully interlocking herringbone pattern etched in the glass, has a similar life, so vivid that one can almost see the greenish color of the vase in the black-and-white photograph.

The second example on the facing page shows the facade of a modern office building. Here the alternation is brutal, banal. The tired yet killing repetition comes from the fact that what repeats is one-dimensional: there is no alternation to speak of, no living centers which repeat. And there are no vital secondary centers repeating between the primary ones.

The difference between the kind of repetition which has life, and supports life, and the kind which is banal, always lies in this matter of the alternation.

In the upper building, Brunelleschi's Foundling Hospital, the round medallions (by Della Robbia) alternate with the columns and column bays. We see the columns repeating; we see the arches repeating; we see the space of the bays repeating; we see the triangular space between adjacent arches repeating; we see the ceramic roundels in these triangles repeating. Each of these things that is repeating is a profoundly formed and living center. The result is beautifully harmonious, and has life.

In the lower building—also a colonnade with columns and bays—there is repetition, but no significant living centers in the repetition. The repetition does not alternate because the centers have no life to make it alternate. The columns repeat, the space between the columns

repeats. But because neither the columns themselves nor the space between the columns form profound centers, there is no beat, no life of genuine alternation. The building is depressing, and dead.

Why is alternating repetition more satisfying, more profound, than simple repetition? One answer lies, once again, in the recursiveness of the rule. For what repeats within a whole is not merely the units. In a whole, the space between the units also repeats. And often even the repetition itself repeats. Thus the rule about the repetition applies to all the elements within the whole. When we apply it to all the elements, to the entities, to the spaces between the entities, and even to the sequences of repeating entities themselves, then there is wholeness in the result.

More exactly, it seems that what is really happening is not repetition, but oscillation. The thing repeats like a wave—one, then the other, then the one again, and so on. In the Ottoman velvet on page 165, the oscillation and alternating repetition has reached tremendous and profound subtlety. The waves with the "lips" oscillate. The triple circles oscillate. The space between circles and lips oscillates and repeats. The overall effect is a profound unity.

This partly explains the deep life of the Japanese raked sand garden. The teeth of the rake make waves in the sand. Then, the repetition of the sand ridges alternating with the repetition of the sand valleys work together with the larger alternating repetition of the design: the waves and whorls made by the moving rake leave, in the sand, the trace of the rake's own parallel and larger alternating movement.

On the next page, Matisse's simple, waving, brightly colored shapes, his trademark, cut out from colored paper, form the same waves and alternations in the space of his picture.

Whenever centers repeat within a structure, they will generally unite to intensify a larger center only when a second system of centers is inserted in between them, forming a second alternating system, sometimes even creating a third system of centers mutually caused by the first two, which once again ripple and alternate and oscillate.

How subtle the alternation has to be in order to work! In the bad examples the repetition does form some kind of alternation, but there is nothing beautiful or graceful about it: it is mechanical. In the good examples, we see a subtle beauty. The life comes about only when the alternating wholes are beautifully and subtly proportioned and differentiated.

FUNCTIONAL NOTES

Examples of patterns in APL which make use of alternating repetition as a source of life are: CITY COUNTRY FINGERS (p. 21), which calls for an alternation of city and countryside; PARALLEL ROADS (p. 126), which calls for an alternation of roads and buildings; PATHS AND GOALS (p. 585), which calls for a regular alternation of paths and stopping points; BULK STORAGE (p. 687), which calls for alternation of inhabited rooms and storage; TERRACED

SLOPE (p. 790), which calls for an alternation of walls and terraces; CLOSETS BETWEEN ROOMS (p. 913), again an alternation of rooms and closets; and NETWORK OF PATHS AND CARS (p. 270), which calls for a complex five-way syncopated alternation of pedestrian paths and the spaces between them, roads for cars at right angles to the paths, and the spaces between them, and a system of nodes where the two networks cross each other.

2.5 / POSITIVE SPACE

What I call POSITIVE SPACE occurs when every bit of space swells outward, is substantial in itself, is never the leftover from an adjacent shape. We may see it like ripening corn, each kernel swelling until it meets the others, each one having its own positive shape caused by its growth as a cell from the inside.

My observations have led me to believe that in almost anything, large or small, the extent to which every single part is positive is fundamental to its life and wholeness. A work of art has life more or less to the extent that every single one of its component parts and spaces is whole, well-shaped and positive. Of all the properties which

create life in space, this is probably the most simple and the most essential, since it is this one which guarantees to every part of space the status of being a relatively strong center.

An almost archetypal example of this positive and coherent state of space may be seen in the 17th-century Nolli plan of Rome. In this plan each bit of every street is positive; the building masses are positive; the public interiors are positive. There is virtually no part of the whole which does not have definite and positive shape. It is a packing of definite entities, each of which is definite and substantial in its own right. This has come about, I think, because each of these places—whether street, square, or block of buildings—has been shaped over time by people who cared about it, and it has therefore taken a definite, cared-for shape with meaning and purpose. Each of these entities has been formed by the slow deliberate strengthening of centers.

In the present Western view of space, we have forgotten the powerful force of space visible in the Nolli plan, even though it was commonplace in almost every ancient culture. We tend to see buildings floating in empty space, as if the space between them were an empty sea. This means that most often the buildings are placed and have their own definite physical shape—but the space which they are floating in is shapeless, making the buildings almost meaningless in their isolation. This has a devastating effect: it makes our social space itself—the glue and playground of our common public world—incoherent, almost non-existent. And the character of positive—that is to say "shaped"—space has been forgotten in private gardens, in rooms, in the space of objects and paintings and textiles—even in the typefaces we use.

Here, in the famous Kizaemon tea bowl, now preserved in Japan, we see the phenomenon in a very subtle case. Looking carefully at this bowl, we come to realize that its beauty lies in the fact that not only does the bowl have a beautiful shape in itself, but that also the space next to the bowl has a beautiful shape. One might even say that the beauty of the bowl is created by

the fact that the space next to it is beautiful. This is an excellent example of positive space at work. In a cruder work of art, the thing is shaped with careful intent, but the space next to the thing is not. The 1960s sculpture of three almost random cubes shown at the bottom, on the facing page, is a typical example of this kind of thing.

Consider two further examples of positive space from Anatolian carpet design. The border of a Seljuk carpet is especially good because both positive and negative shapes are extreme—rather original. And in the field of an Anatolian multiple-niche prayer carpet, every whole is shaped, essentially, by the shape of the wholes which lie next to it, making every part of space positive, composed of living centers. Signifying God, as the carpet does, hence perfect unity, the positive character, the centeredness of every particle of space, is an important practical and spiritual aspect of the carpet's life.

In poor design, in order to give an entity good shape, the background space where it lies sometimes has leftover shape, or no shape at all. In the case of living design there is never any leftover space. Every distinct piece of space is a whole. In Matisse's cut-out blue nude, every part of the space is positive — and hence it has life. In the ancient Mughal frieze below, every bit of space between the flowers and the leaves, even between the veins of the leaves, has its life.

It is especially hard to see positive space in the interior three-dimensional space of buildings. In a building which works well, the various parts are always spatially positive. This means that even closets, small leftover rooms, hallways, and places between rooms all have the quality of being positive, useful, and beautifully shaped. And of course, the same thing continues to the outdoors, so that the various exterior places around the building all have a positive character, each one of them. There is not a single place which is "leftover." We see positive examples in the arcade in Italy shown on the left, and in the great room of a Japanese castle, on the right. But the "modern" space in the other examples fails. The rooms by Louis Kahn, though meant to be interesting and composed in "new" ways to create a modernistic effect, fall apart spatially because there is no positive space in them: and hence no life.

The definition of positive space is straightforward: every single part of space has positive shape as a center. There are no amorphous meaningless leftovers. Every shape is a strong center, and every space is made up in such a way that it only has strong centers in its space, nothing else besides.

FUNCTIONAL NOTES

Detailed functional arguments explaining the functional effects of positive space are given in APL under the discussion of POSITIVE OUTDOOR SPACE (p. 517). Other versions are scattered throughout the text in, for instance, THE SHAPE OF INDOOR SPACE (p. 883); HOUSING IN BETWEEN (p. 256); SHIELDED PARKING (p. 477); SITE REPAIR (p. 508); SIX FOOT BALCONY (p. 781); WINDOW PLACE (p. 833); CEILING HEIGHT VARIETY (p. 876).

The practical issues for a building are straightforward. Rooms and passages which have "neutral" character reduce the life of a building. In a case where every space has positive space, this means that we invent an arrangement of spaces in which all the rooms fit together and yet take the size and shape and form and character they need: each swells to its "perfect" character forcefully, and dramatically, and well; they are not just laid side by side as in a "conventional" plan.

More generally, the main two practical results that happen from positive space in its various forms are (a) that every bit of space is very intensely useful, and (b) that there is no leftover waste space which is not useful. The combination of the two creates well-used, effective space, and therefore a very solid living character throughout the space.

In the built world, large or small, the extent to which every single part of the thing—solid or void—is positive is key to its practical life. Setting tiles, we try to make the grout between the tiles just thick enough to have its own "weight," and thus even in the grout lines we form positive space between the tiles. Making a chair, we use the members to form positive and geometrically simple shapes in the air between the members, because these shapes will be strongest and most effective in the structural frame of the chair.

2.6 / GOOD SHAPE

When I began looking for living structures, I was surprised to find out how often, mixed with other properties, there was an element that seemed to defy analysis: the works contained elements with the most gorgeous, beautiful, powerful shapes. Sometimes this beauty of shape seemed subtle, complex, beyond analysis. I became aware of a special quality that I began to think of as GOOD SHAPE, but could not very easily explain it, or define it.

The fan flowers shown on the brocaded velvet below. The carving of the massive wooden columns in Romania, and its lovely forceful shapes. The intense shape of the Japanese shrine (next page). The powerful shapes even of a simply repeating carved ornament like that on the Abbasid stone relief (next page). For a long time I simply collected these things, and noted that they had good shape. But what did it mean? What is good shape?

It took me a long time to see that good shape itself is also related to the centers; and that, indeed, a shape we see as good is a shape which is itself, as a shape, made up from multiple coherent centers. For example, the beauty of shape in the fan-shaped leaves in the Turkish velvet comes about because of the peculiar way that each individual shape is made from multiple centers.

To make the point quite clear, it may be helpful to pick out two objects, one which has very good shape in itself, the other which strongly lacks good shape. On page 181, the Japanese teapot stand we have studied before has beautiful "good shape" within itself. It has centers in every part of its shape, and it is this which makes the shape good. In contrast, the futuristic chair has quite appallingly bad shape: none of its components are centers, and it is this which makes the shape bad.

What is a "good shape"? What is it made of? It is easiest to understand good shape as a recursive rule. The recursive rule says that the elements of any good shape are always good shapes themselves. Or, we may say this once again in terms of centers. A good shape is a

Abbasid stone relief: what seems like a rather intricate "tracery" design is actually immensely solid, because the shapes—wheels and infill—are made of such simple and solid pieces. The good shape of the ornaments appears in the way that every part, every single part, has positive and definite shape, thus helping the overall organization, and making the large "wheels" magnificent in their resulting shape.

Japanese shrine. The shape is so magnificent, it needs no comment.

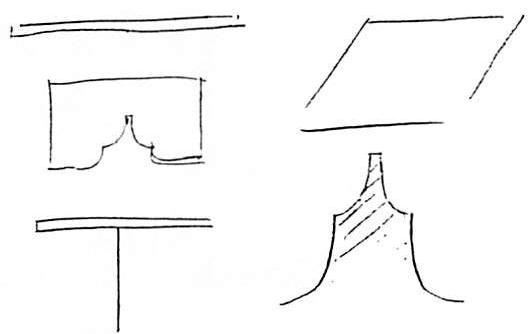
center which is made up of powerful intense centers, which have good shape themselves.

In addition, we note that the simplest and most elementary good shapes are made from elementary figures. Thus the first thing to realize is that in most cases the good shape, no matter how complex, is built up from the simplest elementary figures. The teapot stand can be seen to be built up from the illustrated simple shapes, each of which has good shape. Notice that I include the shape of the positive space under the lip of the teapot stand as one of its component centers.

On the other hand, the amorphous mass of the futuristic chair cannot be understood as being composed of simple elementary shapes at all. If one tries to take it apart, and identify its component shapes, then these shapes are themselves seen to have very bad shape again. In effect, it is not made of centers at all. When space is truly whole, the elements are always made up from shapes which are much more regular in some sense.

Let us start a more detailed understanding by looking at the Persian carpet on the next page. It seems superficially "floral." But on close inspection it turns out to be made up of simpler forms, including triangles, rhombuses, hexagons, arrowheads, pieces of circles, all rather regular—and it is their regularity which allows the formation of so many ambiguous cross-relationships within the form. The shapes of the flowers, leaves, buds, blossoms, stems, are all

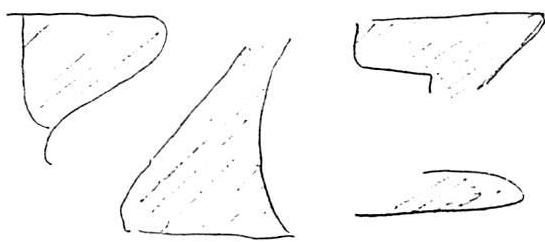
made of geometrically simple shapes, powerful as bits of local geometry. Here even the flower petals are made of elements that are essentially straight line figures, squares, and triangles, both the colored pieces and the triangles, hexagons, etc., put together in very complex ways to create the illusion of organic shapes. Why is this so important? I believe the regularity of the simple shapes creates a potential for much more complex systems of cross-relationships in space which can never be attained by the loose organic kinds of shape. And what seem like complex centers are made of simpler centers which are also alive—and it is these centers above all which give the complex ones their life.

For clarity, here is an extremely simple example, a border ornament from another carpet.

Again it is floral-looking. Yet on close inspection, it turns out to be made up entirely of diamonds, squares, and triangles, both the colored pieces and the space between. The resulting ornament, as a whole, has good shape. The good shape is an attribute of the whole configuration, not of

the parts; but it comes about when the whole is made of parts that are themselves whole in this rather simple geometric sense.

In one sense all this is obvious. We are going to apply the rule that every visible part of the design, at every level, must be a good figure or a strong "entity." This clearly rules out amorphous blobs, vague shapes, etc., and clearly includes squares, octagons, eight-blossomed flowers, 45-degree triangles, etc. But when we try to go more deeply into the matter, and to give a precise rule for distinguishing things which have goodness of shape, it turns out to be hard to define the idea exactly. The following is a partial list of properties required to make a good shape, and for the elements from which a good shape is made:

1. High degree of internal symmetries.
2. Bilateral symmetry (almost always).
3. A well-marked center (not necessarily at the geometric middle).
4. The spaces it creates next to it are also positive (positive space).
5. It is very strongly distinct from what surrounds it.
6. It is relatively compact (i.e., not very different in overall outline from something between 1:1 and 1:2—exceptions may go as high as 1:4, but almost never higher).
7. It has closure, a feeling of being closed and complete.

All in all, in my experience, in the build-up of a good shape the following elements are the most common: square, line segment, arrowhead, hook, triangle, row of dots, circle, rosette, diamond, S-shape, half circle, star, steps, cross, waves, spiral, tree, octagon. The things which we identify as "good" shape are just those complex shapes which are most strongly made up of centers.

All this is subtle when we try to apply it. Take the circle, for instance, a symmetrical compact figure, which would appear to be a "good shape"—or so one would assume. But the circle has great problems. The space next to it is not easily made positive, not easily made into centers—and the circle, when used in a design, can easily then not be good shape at all. We see such

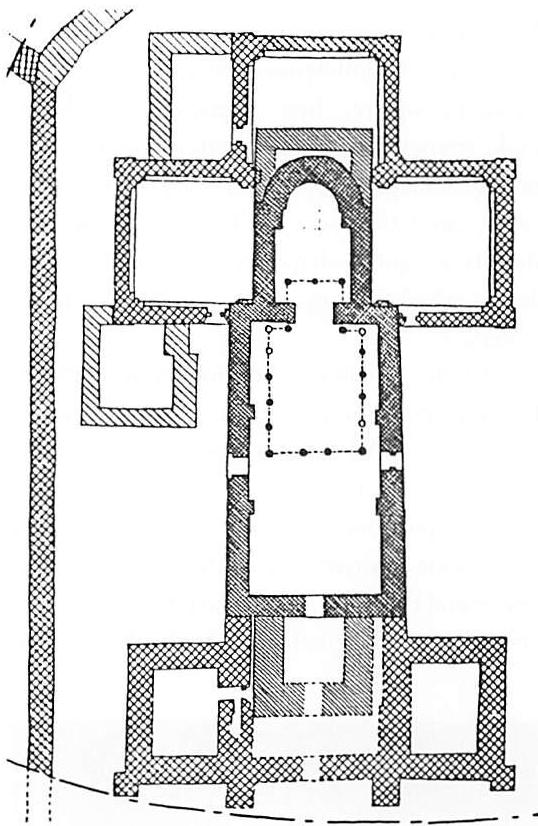
an example in the courtyard of the Copenhagen Police Headquarters building: a ridiculous plan, which is trivial because the space next to the circle is formless, and therefore meaningless. The high degree of sophistication needed to make a circle have good shape is seen in the fabulous Ottoman velvet on page 183, where the two systems of circles are drawn slightly distorted so that the moon shapes, the space between the circles, and the small circles and large circles all work as centers. The pattern is stunning in its power.

Above all, we must remember that the quality of good shape occurs only when the shape itself, as a whole, becomes powerful and extraordinary, when we have good shape by following the principles I have outlined. The ancient classical Greek horse's head, the early Christian church plan, the deeply hewn wooden members in the Romanian log house—these all show good shape in this large, wonderful sense, to the extreme.

The horse especially, with its bulbous eyes, creates an unforgettable shape, hewn as if from three-dimensional living centers. And the early Christian church, almost at the opposite extreme, simple, quiet . . . and yet composed in the same way so that its simple elements together also make an unforgettable shape. How the apse and many squares together, forming locally symmetric pieces in the composition, create all in all something which is matter-of-fact, simple — yet somehow unforgettable, like an ancient haunting melody.

And, perhaps most beautiful of all, this lovely sail from an Egyptian boat has the quality of good shape to an extraordinary degree. We see it and feel it immediately, and we feel the intense and lovely character it has. But — being analytical again — we also see that this complex shape is made up of the furls in the sail, and every one of these — modest, gently curving — is a center in itself. By having good shape, the life of dozens of centers is created. The sail has life because its shape, as a shape, is made up of dozens of good centers.

Although it may seem surprising to someone raised in the mechanist-functionalist tradition, good shape in buildings, rooms, gardens, streets, plays a vital role in the way they work. Essentially, what happens is that the thing which

works effectively has—must have—more centers in it and, by virtue of having more centers, has better shape. So the good shape is not only making things more beautiful; it also makes them work more profoundly, more effectively.

FUNCTIONAL NOTES

Some of the practical arguments which show why good shape makes things work better. We have seen in the last section, things which are alive have good positive space in them. So in a well-working thing, all the space between the parts has to have good shape.

This special rule is really just part of a more general rule, which says that in a thing which is alive almost every visible part, at every level, has good shape, and is therefore a living center. In the leaf we see the shape itself as made up from centers. In a bridge with good shape, the members play an effective and efficient structural role. In a window with good shape, the arch, header, casements, and jambs all play their roles efficiently and well.

In an amorphous blob-like shape, on the other hand, we cannot really see any centers. Thus the shape is not made of centers in any obvious way, does not induce a field of centers in any clear way, and the beauty of function, the clarity and subtlety of the way it works, will be lessened.

The essence of "good shape," then, is that each part of space is positive and definite. As a result we also tend to see simple good figures within a good shape, and good shapes tend to be made from simple figures. This is the basic rule.

Making a dovetail, we choose its shape in such a way that the pieces of wood on both sides are intense centers, in order to preserve the structural integrity of the members. The good shape that results always has a shape just right for structural strength. In a wall with openings, we choose the best shape for the openings, so that both the openings themselves, and the panels between openings, have simple structural integrity. In APL, PATH SHAPE (p. 589), BUILDING FRONTS (p. 593), COLUMN PLACE (p. 1064), and ROOF CAPS (p. 1084), all show examples. As for the actual space in rooms, several arguments are given in APL to show that the shape of rooms, spaces, and streets, in plan and in section, will always play a vital role in the way they work (E.G., THE SHAPE OF INDOOR SPACE, p. 883).

2.7 / LOCAL SYMMETRIES

We have seen that each strong center is a microcosm of the widespread wholeness which can occur in space. In many of the examples, it has been implicit that the presence of a strong center in the field depends, to a great degree, on various interlocking and overlapping LOCAL SYMMETRIES. This happens, most obviously, because the existence of a center and the existence of a local symmetry are closely related. Wherever there is a local symmetry, there tends to be a center. Where a living center forms, it is often necessary to have some local symmetry.

However, the exact relation between life and symmetry is muddy. Living things, though often symmetrical, rarely have perfect symmetry. Indeed, perfect symmetry is often a mark of death in things, rather than life. I believe the lack of clarity on the subject has arisen because of a failure to distinguish overall symmetry from local symmetries.

Observe, first, that overall symmetry in a system, by itself, is not a strong source of life or wholeness. This Rorschach ink-blot, for instance, is a rather weak whole; it has relatively little life as a structure; its centers are poorly developed. The one large symmetry it has, by itself gets you very little.

Observe further that over-simplified overall symmetry in buildings is most often naive and even brutal. The neoclassicist buildings of Mussolini's fascist era are often perfectly symmetrical but, like the ink-blot, have little life in them. Albert Speer's design for Zeppelinfeld, shown here, is another example. And the plan for the Renaissance Center, Detroit, shown opposite, and ac

tually proposed by a real architect, has a similarly rigid and exaggerated symmetry. Obviously this place would not have had much life, if it had been built as drawn. There is powerful overall symmetry in the large composition and in the parts. But we do not experience subtle wholeness. Instead, we experience almost insane rigidity—the very opposite of life.

In general, a large symmetry of the simplified neoclassicist type rarely contributes to the life of a thing, because in any complex whole in the world, there are nearly always complex, asymmetrical forces at work—matters of location, and context, and function—which require that symmetry be broken.

We see this clearly in the Alhambra, shown on this page and the next—a marvel of living wholeness. It has no overall symmetry at all, but an amazing number of minor symmetries, which hold within limited pieces of the design, leaving the whole to be organic, flexible, adapted to the site.

To understand to what a deep extent the beauty of the Alhambra plan lies in the loose

and subtle interweaving of local symmetries, we may compare it with the plan of the Detroit Renaissance Center I have referred to. In the Alhambra, we sense that each room, court, garden, hall, works in its own right—because its local symmetry helps locally to make better space. In the Renaissance Center plan we feel

something quite different: the various aspects of symmetry that appear seem not to be governed by the local needs of each space, but are, rather, extensions of some huge symmetrical scheme which is irrelevant to the character of any particular room or garden, and instead merely reflects automatic and totalitarian reach of a larger scale order which is ultimately irrelevant to life as it arises locally. Thus the real binding force which symmetry contributes to the formation of life is not in the overall symmetry of a

building, but in the binding together and local symmetry of smaller centers within the whole.

The fact that local symmetries work to create coherence, while overall symmetry rarely does, was dramatically illustrated by an experiment I did many years ago while working at the Harvard Center for Cognitive Studies. In this experiment, I compared a number of black and white paper strips, and measured their coherence as felt, experienced, perceived, remembered, by different experimental subjects. The black and white strips I used are shown on page 189, in order of their coherence (as measured by my experiments).

I was able to show that the coherence of a strip depends on the number of local symmetries which appear in its pattern (a local symmetry being defined as a shorter segment of black and white squares within the strip as a whole, which is itself locally symmetrical). Apparently, the perceived coherence of the different patterns depends entirely on the number of symmetrical segments which they contain. Since each of the segments, when symmetrical, is a "local symmetry," I summarized this experimental result, by saying that the most coherent patterns are the ones which contain the largest number of local symmetries.

In another series of experiments my colleagues and I very strongly established the vital role of local symmetries.² (In fact the experiments go rather deeper, and provide confirmation for the existence of the wholeness as an overlapped structure of centers, as I have defined it in chapter 3. But above all, they focus on the key role which local symmetries play in the creation of wholeness.)

The experiments were performed with 35 black-and-white strips seen on a neutral gray background (this page). Each strip was 7 squares long, and was composed of 3 black squares and 4 white squares, arranged in different arrangements. There are 35 possible strips of this kind.

First, we established that the relative coherence of the different patterns—oprationally defined as ease of perception—was an objective quality that varied little from person to person. That is to say, the coherence is not an idiosyncratic subjective feature of the patterns seen differently by different people. It is an objective measure of cognitive processing, roughly the same for everyone.

Second, we were then able to identify the structural feature of these patterns which caused this perceived "coherence." It turned out that the perceived coherence depends, simply, on the number of local symmetries present in the pattern. However, since most of the symmetries are hidden, this feature is far from obvious, and is a deeply buried structure in the patterns.

We first devised various different experimental tasks which were designed to find out which of the patterns people saw as most orderly, most coherent, or most simple, or "as having the most structure." The experimental tasks varied. They ranged from simply asking people which patterns they found most orderly to ways of establishing which ones could be seen, and recognized, most quickly, at very high speeds; from ways of testing which ones could be most easily described in words to ways of testing which ones were objectively easiest to remember, under difficult memory conditions.

We found that, whether we used ease of description, ease of memorization, subjectively

9 local symmetries 9 local symmetries 7 local symmetries 9 local symmetries 7 local symmetries 7 local symmetries 7 local symmetries 8 local symmetries 7 local symmetries 8 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 6 local symmetries 5 local symmetries 6 local symmetries 5 local symmetries 6 local symmetries 5 local symmetries 6 local symmetries 5 local symmetries 5 local symmetries 5 local symmetries 5 local symmetries 5 local symmetries 5

judged "simplicity," or ease of recognition in a tachistoscope, the relative coherences as measured by these different experiments were very strongly correlated. It was therefore possible to combine the rank orders in the different experiments to create an overall rank order of perceived cognitive coherence for the 35 strips.

From this first series of experiments, two important results emerged. First, in any one experiment, the relative degree of coherence seen in different patterns was rather constant from person to person. This means that the coherence is not a subjective thing seen differently by different people. People agree about it. Second, the relative coherence of the different patterns, as measured by the different experiments — even though these experiments were based on widely different kinds of cognitive processing — remained roughly the same.

Taken together, these two results indicated that the relative coherence of the patterns is an objective matter of cognitive processing, independent of the person who is judging, and independent of the particular kind of experimental judgment which is used to measure it. It is therefore possible to construct a single overall order of coherence for the 35 patterns. The photograph on page 189 shows the strips in order of perceived coherence, the most coherent at the top, the least coherent at the bottom.

For three or four years after completing this experiment, I worked almost continuously to find some structural feature of the 35 black and white patterns which would explain the rank order of coherence of the different patterns. What do the more coherent ones have in common? What do the less coherent ones have in common? To solve this problem, I would try some measure of orderliness, then calculate this measure for the 35 different patterns, and then see if the rank order which this measure generated was the same as the one we had obtained earlier, experimentally.

It was an extremely difficult thing to do. The crux of the problem lay in the fact that, among the 35 strips, the "good" ones are of very different

types. One, for instance, is completely symmetrical, and has the black and white squares alternating. Another is completely asymmetrical, and has all the black squares together in a lump, and all the white ones together in a lump. Others have both lumpiness and overall symmetry. Others have neither.

Since lumpiness and symmetry were two of the main explanations for cognitive simplicity in common currency around 1960, it was hard to get beyond these features. I tried various combinations of the two, but always concentrated on lumpiness and on overall symmetry in some combination.

It took me three or four years to find the right answer. The reason is that local symmetries (as opposed to overall symmetry) were not under discussion at all in the literature. Further, the local symmetries are nearly invisible in the pattern — they do not jump out at you, but are lost, rather as children's tiger-in-the-trees pictures confuse the eye and make you lose the tiger.

Further, it was quite unclear how to unite the idea of symmetry with the idea of large lumps. It was this that finally gave me the key, when I realized that both overall symmetries and large lumps actually contain more local symmetries inside them. For instance, a lump of white that is four squares long is symmetrical, overall. But it also contains three symmetrical segments that are two squares long and two that are three squares long, making—with the four-square long lump itself—a total of six local symmetries. Five of them are hidden. But, even though hidden, the local symmetries are capable of being counted and measured to show both the presence of overall symmetry, and the presence of large lumps. Two other examples are shown on the opposite page.

So, after four years of work, and hundreds of tries, I found a very simple measure which correlated very strongly (in fact almost perfectly) with the ranked coherence of the different patterns.

This measure is the number of local symmetries which the pattern contains. To count the local symmetries in one of these strips, I considered the strip as made of seven adjacent squares. There

are, within a strip, twenty-one connected segments made of two, three, four, five, six, or seven adjacent squares (just one segment that is seven squares long, two segments that are six squares long, three that are five squares long, four that are four squares long, five that are three squares long, and six that are two squares long—twenty-one connected segments in all). In any particular strip, with a particular pattern of 3 black and 4 white squares, we can examine each of these twenty-one segments, one by one, and ask if it is symmetrical or not within itself. I called each symmetrical segment a subsymmetry of the pattern. Among the 35 strips made of 3 black and 4 white squares, the strip with the highest number of internal symmetries has nine subsymmetries among its twenty-one segments. The strip with the lowest number has five subsymmetries.

I have displayed the number of subsymmetries that are in each strip opposite the picture of the strip, in the photograph on page 189. The 35 strips are arranged in the overall combined order of perceptual coherence. To the right of the photo is the number of subsymmetries the strip contains.

As we see, the strips which are most coherent experimentally also have the highest numbers of subsymmetries to within a high degree of correlation. Those strips which are least coherent experimentally have the lowest number of subsymmetries. The number of local symmetries the pattern contains essentially predicts how "good" it is.

The measure is subtle and refined. Even in the most coherent patterns only 9 of the 21 segments are symmetrical. And in the least coherent patterns 5 of the 21 segments are symmetrical; so the number of subsymmetries varies only modestly from pattern to pattern. Nevertheless, the way it varies mirrors, almost perfectly, the actual cognitive coherence as measured by experiment.

It is important that I stress once again that this result has little or nothing to do with the overall symmetry of the design. At the time I analyzed the original experimental data and first discovered the relation between local symmetries

and perceived coherence, I also tested another criterion, in which the symmetrical segments are weighted by their length. In this second criterion, the longer a symmetrical segment is, the more points I gave it, and the strips with large overall symmetries thus got extra points in this measure. I found out that this second criterion correlates less well with the experimentally measured coherence. Apparently large symmetries do little to contribute extra coherence to a pattern: what matters more is the number of smaller—i.e., local—symmetries.

Why does the presence of many local symmetries in the design make it coherent and memorable? It is as if the symmetrical segments act as a kind of glue—the glue which holds the space together. The more glue there is, the more the space is one, solid, unified, coherent. And notice one more detail: for the glue to be effective, it seems that many of the symmetrical segments must overlap. They are by no means discrete or disjoint. One symmetrical segment

overlaps another — and it is not only the number of symmetrical segments, but also their continuous overlapping which makes the glue that makes the design “whole.”

These experiments played a very big role in my own effort to find a theory of wholeness, since it strongly confirmed my growing suspicion that the wholeness in the world is in some fashion a structure of overlapping wholes. Note that the subsymmetries are not distinct, but overlap within any one pattern. It is this overlapping

structure of perceived entities, in this case defined by their local symmetry, that forms the salient wholeness which is perceived and felt. In later years the entities (seen in the experiments only as local symmetries) were extended to be wholes, and later centers, to provide the underpinning of the theory in its entirety. What is essential is that the local symmetries in these patterns play a decisive and quite unexpected role. Though hidden from view, they essentially control the way the pattern is seen and the way it works.

Look again at the plan of Alhambra. It illustrates the point magnificently. The Alhambra's plan, overall, is wildly asymmetrical, it has nothing in common with the excesses of neoclassicism—it is free, free as a bird. Yet in its detail, it is simply full of symmetries at many levels. There are courtyards which are internally symmetrical, rooms which are symmetrical, pieces of wall, windows, columns, which are symmetrical—the plan is a maze of intricate and subtle smaller symmetries, symmetries of segments or subsymmetries, yet none of this ever creates that dead and lifeless overall neoclassicist symmetry of which we should rightly be afraid.

On a smaller scale we see the very same thing in a row of Amsterdam canal houses. The row of houses as a whole is not symmetrical. Nor is any one house, taken by itself, perfectly symmetrical, neither in its plan, nor in its front facade. Yet both in plan and in elevation, each house, and the row of houses as a whole, contains vast numbers of powerfully symmetrical elements put together, so that the feeling of symmetry and order pervades the structure. It is the local symmetries which cause its beautiful order.

What is the relation between symmetries and centers? How do symmetries allow centers to intensify each other? In many cases, a symme

try is used to establish an elementary center. Indeed, an overwhelming majority of centers are locally symmetrical. Each local symmetry establishes a symmetry between two smaller centers to create a larger center. Indeed, one might almost say, "When in doubt, make it symmetrical." Most centers become stronger when symmetrical, except, of course, that symmetries must not be used to smooth out real asymmetries in external conditions, and must always be true to the local conditions.³

However, provided that the irregularity of the local context is not violated, local symmetries provide a glue which binds the field of centers, thus making centers more coherent. We see this in the primitive and beautiful pattern of the 9th-century illustration from the Book of Kells, where an apparently irregular field is disciplined by the powerful presence of many symmetries and symmetrical structures—yet the whole thing is strongly asymmetrical, bent by its own laws, formed by the process of growth in the draftsman's hands.

If we want to create or intensify a center, we can always most easily do it by making a local symmetry between other centers. And, in practice, the easiest way to make a complex thing is often to make it up out of regularly shaped pieces, and then patch in any irregularities.⁴ This method of composition is illustrated by the incredible Persian tilework on the left, where very simple symmetries are chained together in this wild and powerful composition, replete with new centers which the symmetries have formed.

FUNCTIONAL NOTES

Among functional examples, a rough fence on a rough terrain is most easily made from pieces of wood that are square and vertical, patched with connectors to make up for the unevenness of the terrain. The same thing is true with built-in furniture, where we often build regular symmetrical cabinets, and then cover the irregularities where the cabinet is fit to the room (which is usually not perfectly square) with trim.

On a more significant level, the same is true in very much larger environmental issues. For example, in APL, LACE OF COUNTRY STREETS (p. 29) relies on the symmetry of roads, and squares of countryside between the roads, to provide its regular structure. CIRCULATION REALMS (p. 480) uses symmetrical centers as the core centers for circulation to provide clarity of movement in a complex urban space. Streets, obviously, are made symmetrical, with departures from the symmetry as needed by unusual junctions, buildings, gardens, or terrain (PROMENADE, p. 168, ROW HOUSES, p. 204.) And rooms, too, should most often be symmetrical, to start with, with minor modifications then patched in, to correct for odd situations (THE SHAPE OF INDOOR SPACE, p. 883).

2.8 / DEEP INTERLOCK AND AMBIGUITY

In a surprisingly large number of cases, living structures contain some form of interlock: situations where centers are "hooked" into their surroundings. This has the effect of making it difficult to disentangle the center from its surroundings. It becomes more deeply unified with the world and with other centers near it.

The hooking effect is sometimes done literally, as in the giant star ornament from the tilework of the Tabriz Mosque (page 198). At other times, a similar unification is accomplished through the creation of spatial ambiguity, an ambiguous zone which belongs both to the center and to its surroundings, again making it

difficult to disentangle the two. A common example of this situation in building is the house with a gallery or arcade round it (photograph on next page). In both cases, a center is enmeshed with its surroundings, and therefore achieves more life. I think of the relation between the center and its surroundings, in both cases, as DEEP INTERLOCK AND AMBIGUITY. The center and its surroundings interpenetrate each other, using intermediate centers which belong to both of two adjacent larger centers.

As in the photographs below, the different elements in a work seem to reach out and grip each other. In buildings, the space outside the building

reaches in and grips the building anywhere where it is surrounded by a gallery or an arcade. The space in the gallery belongs to the outside world, and yet simultaneously belongs to the building — thus causing a fusion of the two. The center which is the building is linked to the center which is the volume of the arcade. The space of the outside, and its center, is linked to the center which is the volume of the arcade. Thus the space of the arcade and its center form a bridge which links the two centers on either side in an indissoluble knot. The interlock, or ambiguity, strengthens the centers on either side, and they get their strength from the strength of the center in the middle.

It is fascinating to see the interlock of the tilework on the great ornament of the 16th-century Tabriz Mosque side by side with the interlock in the yellow brush strokes in the famous painting by Pierre Bonnard, L'Atelier au Mimosa (painted 1939-46), and following the magical interlock on the surface carving of the Shang bronze (2,500 B.C.). The use of interlock goes on and on. It has no time and no place.

FUNCTIONAL NOTES

A great many practical examples of deep interlock and ambiguity are given for many scales in APL. The principle creates fusion and connection at an enormous number of scales in the physical world, from the largest regional scale to the tiniest physical detail.

A practical example of the way deep interlock works on a very large scale indeed, the regional scale, is given in the discussion of city and country in CITY COUNTRY FINGERS (p. 21), or of city and industry, INDUSTRIAL RIBBON (p. 227). On the scale of buildings we have a similar phenomenon in the way that indoor and outdoor space must interlock deeply, to provide the building with the proper light for all its rooms. Rooms with light on two or three sides are the most likely to be alive (WINGS OF LIGHT,

LIGHT ON TWO SIDES OF EVERY ROOM, pp. 524, 746). This requires a structural relation between the centers inside (the space itself), centers in the walls (the windows), and the centers on the outside (centers in exterior space).

The ambiguity between indoors and outdoors in a building is also crucial for social reasons, thus leading to yet another typical kind of interlock between indoors and outdoors which we know as arcades and terraces. This

is described explicitly under the functional arguments for arcades and terraces (ARCADES, p. 580; PRIVATE TERRACE ON THE STREET, p. 664). Other examples include WINDOWS WHICH OPEN WIDE (p. 1100), where the interlock is physical between the casements and the air outside, or TRELLISED WALK (p. 809), where it exists between the lattice-work of the trellis and the space around it with which it interlocks.

2.9 / CONTRAST

Another feature I have found repeatedly in works of art which have great life is a surprisingly intense CONTRAST—far more contrast than one imagines would be helpful or even possible to sustain. The following examples show contrast at its extreme.

Life cannot occur without differentiation. Unity can only be created from distinctness. This means, that every center is made from discernible opposites, and intensified when the not-center, against which it is opposed, is clarified, and itself becomes a center. The "opposites" take many forms. But in all of them, contrast of some kind is visible. And in order for the thing to be truly whole, the contrast has to be pronounced. Black-white and dark-light contrast are the most common kinds. Empty-full, solid-void, busy-silent, red-green, and blue-yellow are all possible forms of contrast, too. However, the most im

important contrasts do not merely show variety of form (high-low, soft-hard, rough-smooth, and so on) but represent true opposites, which essentially annihilate each other when they are superimposed. In some sense, it is the contrast—awareness of silence created by a hand-clap—which is going on here. The difference between opposites gives birth to something. This is the origin of yin-yang, active-passive, light-dark.

The three examples shown opposite exemplify the beauty which can be created by contrast, in silhouette (the gate), in spacing (the arabic calligraphy), and in the intensity of color (especially the blue) which is achieved by the forcefulness of the neighboring black and white contrast.

On page 202 the example of a Shaker schoolroom shows how contrast actually works to create life. In the schoolroom the contrast be

tween the dark wood and the light plaster is used throughout the room to bring it peacefulness and unity. Next to it is a very different case of a recently built lobby where the contrast destroys life instead of creating it. The lobby example shows how violent contrast exists between the light of the sky and the dark of the stair against the windows, but the contrast fails completely to make life. If anything, it does the opposite.

In the case of the Shaker schoolroom, the contrast is used, again and again, to make the various centers unified. For instance, the two bands of wood above shoulder level, because of the contrast, form a definite center which would not be there or felt so strongly—if the wood were pale, or painted. The center which is so formed helps the room to become one, unified. You can see how much less unified it would be, if this center were not there, by placing your finger over it. The contrast, instead of separating things, brings them together. In the same way, the contrast between the plaster of the wall and the darker wood of the platform and wainscot creates centers whose opposition (only apparent) actually relates them, unites the wall and the floor, and unites the school benches with the space of the room. Again and again in this example, the contrast helps the centers become unified with one another.

In the glaring lobby staircase, on the other hand, something quite different is going on. Here the contrast—between dark stair and

bright window—does not unify, but separates. This is because it is a kind of contrast which is merely accidental, perhaps even foolish. It is not contrast created in order to help centers become alive. It is either a mistake, or an eye-catching device. And for this reason it fails.

I use this rule to help people understand the fifteen properties: "Draw diagrams, make experiments, in which you try to make something, sketch something, which has the property in it. But it is not enough to catch the property as you believe it is defined. To succeed, you must make a thing which has the property, and which gains deeper feeling because of the presence of the property. Only when you have managed that, can you be sure that the meaning of the property has not eluded you." In this case, for instance, if you thought that making a dark stair against the light was an example of contrast, you could check yourself, and realize your mistake, when you see that the property used in this way fails to make something with deep feeling. Only when you reach an example like the Shaker schoolroom, or the Tuscan church on the next page, by using the property, can you make the thing have a deeper feeling, can you say you have grasped the property.

There can be many other kinds of contrast which have an effect. In functional situations, two materials will often work best together when they are entirely different, so that each one can

take care of its own function. For instance, take the leather top and lacquered surface on a desk. The lacquer is clean and beautiful on the woodwork; the leather is soft and rich. Each one does most effectively what it needs to do. In the plan of Rheims cathedral (next page) we even see a contrast between the massive outer piers and the slender inner piers, which plays a great role in the created unity and life of the church as a whole.

For functional and cognitive clarity, contrast is also practically necessary: the shop in the neighborhood is different from the houses next to it. The front door is different from the back door. The roof is different from the wall. The kitchen is different from the living room. The light in the bedroom is different from the light in the passage. In case after case evidence suggests that the sharp extended and visible differences between things which are different allows each center to take its proper nature. It permits more intensive attention to individual functions. And it creates a feeling of distinction which relaxes people, because it acknowledges and permits different dimensions of experience.

Contrast is the thing which creates differentiation, and allows differentiation. It is the differentiation of the void which gives birth to matter. All differentiation requires that contrast is created in space, in order to give birth to anything at all.

FUNCTIONAL NOTES

In APL the importance of contrast between different human groups is emphasized in MOSAIC OF SUBCULTURES (p. 42); the contrast between work and housing, and the need for the two to feed each other, is discussed in SCATTERED WORK (p. 31); the complementary contrast between space and structure, and the way each defines the other, is described in STRUCTURE FOLLOWS SOCIAL SPACES (p. 940). More detailed necessary contrast, in light and dark for instance, is defined in TAPESTRY OF LIGHT AND DARK (p. 644), and POOLS OF LIGHT (p. 1160). More subtle kinds of contrast, and their effects, are described in WINDOWS OVERLOOKING LIFE (p. 889) and THE FIRE (p. 838).

2.10 / GRADIENTS

You have noticed, I am sure, that almost anything which has real life has a certain softness. Qualities vary, slowly, subtly, gradually, across the extent of each thing. GRADIENTS occur. One quality changes slowly across space, and becomes another.

Gradients must arise in the world when the world is in harmony with itself simply because conditions vary. Qualities vary, so centers which are adapted to them respond by varying in size, spacing, intensity, and character. Daylight varies from the top floor of an urban building to the bottom floor: both windows and ceiling heights will probably have to adapt to these conditions by varying ceiling height, by varying window size — perhaps, too, by varying window character.

Gradients will follow as the natural response to any changing circumstance in space, as centers become adapted correctly to the changes which move across space: in doing so, they will vary systematically, thus forming gradients. These gradients will also form centers because the field-like character which is needed to make every

strong center is precisely that oriented, changing condition which "points" towards the center of the center, forms the center, establishes it, and makes the center real as a field. So, in adapting to the changing circumstances, and therefore making a series of graded centers, still further and larger centers are created.

Look at the examples illustrated here. Window sizes vary from the top to the bottom of a building. There is a gradient in the lengths of fingers on a hand. The spacing and pattern of the ironwork in the gate varies from the bottom to the top. The depth of the rills in the ancient Persian glass bottle vary from the neck, where they are small in proportion to the size of the bottle, to the lower part where the bottle diameter is greater and the rills therefore become larger, too. Shape, line, size, spacing, all vary gradually, not suddenly, in the progression across the thing. All these have life in them.

Buildings and artifacts without gradients are more mechanical. They have less life to them, because there is no slow variation which reveals the inner wholeness.

In something which has life, there are graded fields of variation throughout the whole, often moving from the center to the boundary, or from the boundary to the center. Indeed, gradients are essentially and necessarily connected to the existence of a living center. Almost always the strengthened field-like character of the center is caused, in part, by the fact

that an organization of smaller centers creates gradients which "point to" some new and larger virtual center. Sometimes the arrows and gradients set up in the field give the center its primary strength.

For example, in the subtly drawn cornice on page 205, the few lines of varying thickness which form the bands that generate the cornice set up a gradient in the building. This gradient, or progression, orients the eye towards the top. Thus we see and feel the top of the building coming. The gradient which is created both signals and produces the beginning of the boundary. And by creating this gradient, the building itself—the mass of the building below this cornice—is made more of a center, is a more powerful center. It is the gradient, in this case, which gives that center its life. We see similar phenomena in the gradient of roofs from the Norwegian stave church; in the progression of windows as we move upwards through the German half-timbered house; in the railings of the Greek ironwork; in the variation from finger to finger in Leonardo's drawing of hands.

It is also worth saying that, although gradients are commonplace in nature (see also chapter

6. and in much traditional folk art, they are nearly non-existent in much of the modern environment. That is, I think, because the naive forms of standardization, mass-production (room height determined by 8-foot sheets of plywood) and regulation of sizes (zoning, bank rules, and so on) all work against the formation of gradients, and almost do not allow them to

occur in buildings or in neighborhoods. As a result, one of the most powerful, and necessary, forms of life has been almost removed from the environment.

The beautiful gradients in the openings of the Golden Gate Bridge towers occurred because the high cost of the bridge and the importance of structural efficiency made specialized steelwork

necessary. But this beautiful example is a rarity in our time.

A true gradient requires that the morphology of elements—walls, columns, roofs, windows, eaves, openings, doors, stairs—are able

to exhibit sustained and gradual change of size and character, as one moves through the environment, or through a building. This requires new forms of making, production, manufacture, which are at present only in their infancy.

FUNCTIONAL NOTES

A geometric gradient must occur in the environment almost any time that a true "field" exists with respect to any functionally important variable. As a result, it is one of the most noticeable features of any building complex or building which has life, that we find these examples of steady variation within them. For instance, variation in window size, from the bottom to the top of the building; variation in size or type of tile, or height, or slope, according to the position of a roof (CASCADE OF ROOFS, p. 565); variation in column size and beam size according to the spans (FINAL COLUMN DISTRIBUTION, p. 995); variation in door handle size, even, according to the importance of a door; or variation in door size, cabinet size, shelf size, with height; door size, with importance and distance from the center; plank size, with location in the building; tile size, with roughness of usage of an outdoor area. In each case, the gradient in the smaller centers helps to intensify the life of the larger center which the gradient points towards.

In large-scale engineering we use different-sized members in a frame, to use steel in the most economical way. In the towers of the Golden Gate Bridge there

is a fine gradation of cell size, member size, and plate thickness, from the top of the tower to the bottom, to economize on steel, and place the most material where it is needed most by stresses. A similar thing is described in APL under FINAL COLUMN DISTRIBUTION (p. 995).

At the city scale a gradient occurs, for instance, in the density which falls off systematically from an urban center (DENSITY RINGS, p. 156), and in the relative position of the local center with regard to its catch basin and the line towards the center of the region (ECCENTRIC NUCLEUS, p. 150).

It must occur, also, when we have a sequence of objects that change in size—or in their spacing—as may occur, for instance, in a sequence of rooms, which goes from a small one to a larger one, and from more public to more intimate (INTIMACY GRADIENT, p. 610; ENTRANCE TRANSITION, p. 548; and DEGREES OF PUBLICNESS, p. 192). And it occurs in a molding when a sequence of large and small pieces, next to each other, forms a more fitting edge. It does so by setting up a gradient which points toward the middle.

2.11 / ROUGHNESS

Things which have real life always have a certain ease, a morphological ROUGHNESS. This is not an accidental property. It is not a residue of technically inferior culture, or the result of hand-craft or inaccuracy. It is an essential structural feature without which a thing cannot be whole.²

The Persian bowl below gives us an example. The interior of the bowl is covered by small designs (sinekli), made of two blobs and two strokes, each one a very rapid brush-stroke. When we look at the bowl, we are struck by the beauty of the placing of these brush-strokes, which are of course not perfectly identical. They are rough, in the sense that the size of the individual brush-strokes, their exact spacing, and the exact shape and length of stroke all vary from one to the next, continuously, throughout the fabric of the design.

It is intuitively clear that this subtle variation is partly responsible for the charm and harmony of this bowl—but once again, we are apt to misunderstand it, misinterpret it, because we probably attribute this charm to the fact that the bowl is handmade and that we can see, in the roughness, the trace of a human hand, and know therefore that it is personal, full of human error.

This interpretation is fallacious, and has entirely the wrong emphasis. The reason that this

Persian bowl showing roughness in the beautiful drawing of the ornaments; they vary in size, position, orientation, and according to the space formed by neighboring ornaments, and so make the space perfectly harmonious.

roughness in the design contributes so greatly to the wholeness of the bowl is that a perfect triangular grid of the kind used here, cannot be made to fill a spherical surface properly. If the design were composed of identical units, identically placed, it would break down, and there would be really difficult problems where the grid became tighter toward the center of the bowl. Thus, for instance, near the center of the bowl, there are rows where an extra brush-stroke is squeezed in to overcome the mathematical impossibility of bringing the triangular grid near the center of the bowl. And at these places where the strokes are close together, they are also made smaller, to compensate for the way that they are crowded. If the design was perfectly "regular," this would be impossible.

Indeed, throughout the design the subtle variation of the brush-strokes and their spacing, are done in such a way that each brush-stroke has a size perfectly suited to its place, and each one is placed, by eye, just exactly where it needs to be to create the most beautiful and positive white space between the strokes. When the painter painted the strokes, he could do this almost without thinking, because his hand and eye were so well coordinated—it does not require very intense intellectual effort—but still, it is this which makes the bowl so perfect, and this simply could not be obtained if the brush-strokes were all exactly the same size, or placed at exactly equal intervals.

To continue the same point, compare, on the next page, the beautiful hand-drawn tiles from the mosque of Kairouan with the banal repetition of the postmodern painting of brickwork. The repetition of the tiles (shown in color in chapter 1) is lovely, subtle, heartwarming, and pleasant. The repetition of the brickwork is unpleasant, nearly frightening. Above all the tiles are wholesome. There is a profound feeling of unity in them. On the other hand, the brickwork feels unwholesome, dead; there is only the slightest feeling of unity there. The difference in feeling between the two arises in large measure from the roughness of the one and the sterility of

the other. But this roughness is not merely an accidental feature of the tiles and of other living things. It is an essential feature of living things, and has deep structural causes.

Consider the example on page 213: the wavy border of a carpet, and the way the border design is handled at the corner. Often the border of an ancient carpet is "irregular" where it goes round the corner; that is, the design breaks, and the corner seems "patched together." This does not happen through carelessness or inaccuracy. On the contrary, it happens because the weaver is paying close attention to the positive and negative, to the alternating repetition of the border, to the good shape of each compartment of the wave and each bit of open space — and makes an effort all along the border to be sure these are "just right." To keep all of them just right along the length of the border, some loose and makeshift composition must be done at the corner.

If the weaver wanted instead to calculate or plot out a so-called "perfect" solution to the corner, she would then have to abandon her constant attention to the right size, right shape, and right positive-negative of the border elements, because these would all be determined mechanically by outside considerations, i.e., by the grid of the border. The corner solution would then dominate the design in a way which would destroy the weaver's ability to do what is just right at each point. The life of the design would be destroyed.

All the examples show how the seemingly rough solution—which seems superficially inaccurate—is in fact more precise, not less so, because it comes about as a result of paying attention to what matters most, and letting go of what matters less. As the power of this completed carpet clearly shows, a perfect corner does not matter nearly as much as the correct balance and positive space in the border. The seemingly rough arrangement is more precise because it comes from a much more careful guarding of the essential centers in the design.

In a man-made thing, another essential aspect of the property of roughness is its abandon. Roughness can never be consciously or deliberately created. Then it is merely contrived. To

make a thing live, its roughness must be the product of egolessness, the product of no will. The green tile array from the mosque of Kairouan has this quality. One feels that the different tiles were picked from a pile of slightly different kinds of tiles, or that they were made specially, but once again in a spirit of childish abandon — certainly not with a careful, contrived desire to make it “interesting.” In this sense, roughness is

always the product of abandon—it is created whenever a person is truly free, and doing only whatever is essential, whereas the artificial, excessively formal, careful, calculated quality in a thing always comes about when the person is not sufficiently abandoned, and not free.

This quality of abandon, which exists in roughness, is embodied beautifully in a story which Soetsu Yanagi tells, of his visit when he was young to the workshop of an elderly Korean maker of wooden bowls. The old man was a great master, and Yanagi describes his awe at being allowed to meet the master. As he describes it, he went to visit, and was horrified to see that the old man, so much revered, was using green wood to turn his bowls. At first he does not dare even to mention it—since any question about it would imply a criticism—but finally he plucks up his courage, and says to the master: “You are using green unseasoned wood—and the sap is still flying out of the bowls as they are turned. Will it not cause the wood to split, and check, and crack?” he asks. The old man, without turning a hair, simply says, “Yes, some

times." And the young man, again, hardly dares to say what is on his mind, but finally plucks up his courage, and stammers, "But, but what happens then, what happens if one of the bowls is checked or cracked?"

"I patch it," says the old man, calmly, and goes on with what he is doing.

That is all. It does not mean that the old man doesn't care about the bowls he makes. But he is deeply relaxed about it, not panicked. And in this state where nothing is quite so important, nothing is so terribly, heart-twistingly vital, he knows that he can let the greatest beauty show itself—

and this is the only state of mind in which the property of roughness and the breath that lies in a thing which has the "it" in it can ever come to life.

Going back to the more fundamental meaning of the property of "roughness," a person can only allow the regularity or order of a situation to be let loose, according to the wholeness which is required, when he or she is in this very special state of mind, this egolessness, which allows each part to be made exactly as it needs to be. Roughness does not seek to superimpose an arbitrary order over a design, but instead lets the larger order be relaxed, modified according to

the demands and constraints which happen locally in different parts of the design.

It is certainly noticeable that all great buildings do have various small irregularities in them, even though they often conform to approximate overall symmetries and configurations. By contrast, buildings which are perfectly regular seem dead. This arises because real things have to adapt to irregularities in the exterior environment correctly. They become partially irregular in response. If I have a paintbrush loaded with

paint and want to make a line of dots, I will splash them down, and indeed create a rhythmic line. But of course, the spacing is imperfect, the line is not perfectly straight, because I don't need those things. By paying attention to the global structure only to the extent that is needed, a much more fresh and vital line comes into being.

In the illustrated examples of traditional buildings and town plans shown here this roughness, as a form of perfection, is profoundly visible.

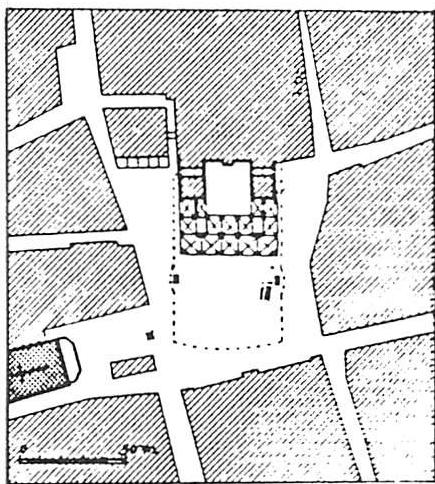
The house shown on page 214 summarizes the whole situation. To build this house correctly, it naturally takes on an apparent roughness. Our current tendency is to dismiss this house as an archaic building, rough only because the techniques of fabrication forced it to be rough because the techniques could not be precise. A future view may reverse this instinct, and recognize that a still more modern house will have this appearance again, because the size, spacing, orientation, and even modified right angles which are visible in the structure all come about as part of a more encompassing exactness of adaptation. More modern construction techniques that will be available in the future, will, like nature, once again be more capable of making such an organic structure and we shall, by then, no longer be ashamed of it.

FUNCTIONAL NOTES

Practical examples of the need for roughness abound. If I am trying to place windows in a building wall with real care for the light in the different rooms, for different views, sunlight and privacy, then the simple row of repeated windows is likely to need modifying, somewhere along its length, to cope with these practical necessities (APL, NATURAL DOORS AND WINDOWS, p. 1046.)

And the beautiful thing is this: the kind of

roughness which comes from this sort of attention is always the beautiful, unselfconscious kind, which is almost perfect — but not quite — and is therefore so harmonious. When framing a house in two-by-fours it is easiest to place them at equal intervals, and set the last one to a different dimension. It would be crazy to try and space them all at equal intervals, 14 3/4 inches apart.

On another scale, Camillo Sitte's famous empirical study of urban space showed clearly how the life of a public square depends on its geometry. As he found: "Public space is often irregular. The irregularity helps to create an informal atmosphere, which links the square to the town and buildings." Camillo Sitte, THE ART OF BUILDING CITIES. But, even in spite of the irregularity, the feeling of centeredness also needs to be emphasized and bolstered by local symmetries in the overall formation of axes, by the placing of things near the middle of squares, and by the use of obviously potent symmetrical building fronts to mark important positions and directions.

There are many indications that too careful a plan, too rigid an order in which each thing is supposed to take its proper place, actually works against function and inhibits proper adaptation. For example, in a building where each room must be the same size and must open off a certain main corridor, rooms may get squeezed, and lose their optimal relationship to sun and light. If they are allowed more roughly to go wherever they can, a more

happy-go-lucky condition, then each one can be placed exactly where the best sun and light are. But the result of this dramatic and careful attention to functional detail is a certain roughness or freedom in the plan. It cannot tolerate the extra constraints of formal concepts in the plan. Here is an example of the way that roughness allows one center to intensify another. The roughness of dimension allows the space between the buildings to sustain the centers which are formed by sun and light.

In APL there are a number of patterns determining necessary functional relationships which have their origin in the idea of roughness. For example SOMETHING ROUGHLY IN THE MIDDLE (p. 606) requires a focus in the middle of a square, but only in an approximate middle, since the position needs to meet other important criteria such as visibility from different streets coming into the square. GARDEN GROWING WILD (p. 801) allows an organic harmony in a garden to be intensified by roughness. SOFT TILE AND BRICK (p. 1141), ZEN VIEW (p. 641), HALF-HIDDEN GARDEN (p. 545), and LAPPED OUTSIDE WALLS (p. 1093) all introduce a subtle roughness into different situations of material, view, position, and surface, to get the best functional effect. FLOOR-CEILING VAULTS (p. 1027) shows how the most perfect vault for a given room, though not rigidly perfect in geometrical shape, arises from an adaptation between the room configuration and the vaulting process.

2.12 / ECHOES

In the course of examining things which have profound life, I have found that there is almost always one vital characteristic, very hard to describe accurately, and yet crucial. In general terms, there is a deep underlying similarity—a family resemblance—among the elements, so deep that everything seems to be related, and yet one doesn't quite know why, or what causes it. That is what I mean by “ECHOES.” Echoes, as far as I can tell, depend on the angles, and families of angles, which are prevalent in the design.

When echoes are present, the various smaller elements and centers, from which the larger centers are made, are all members of the same family; they contain echoes of one another; there are deep internal similarities between them which tie them together to form a single unity.

This family resemblance can be illustrated most easily by a negative example: the building by Michelangelo shown below is, of all the build-

ings I know, the most hopeless hodgepodge. It is a salad of motifs and elements. Squares, circles, broken circles, triangles, are pasted together in a riot of disharmony. The angles are all different. The shapes made by the angles are all different.

Compare Michelangelo's building with the Turkish prayer carpet, where all the motifs—no matter what their differences and powerful differentiations—have a single guiding feeling. They all seem cut from the same cloth, poured from the same mold. The forms in the carpet are dominated by the basic cartouche shape, with elements derived from the lines that form a star-octagon (a combination of alternating right angles and 45-degree angles), in the flower trellis, in the field shape. The same feeling, caused by this combination of angles, also exists even in the fleurs-de-lys of the main border, which are superficially quite different in shape and character, but which are once again made of the same combinations of right angles and 45-degree angles that appear in the cartouche.

Both the carpet and Michelangelo's building were made around 1500. But the first is a

nearly dead chaos virtually without real life; the other is harmonious and living.

In the simpler cases of ECHOES, we see the family resemblance in the different parts because they are simply similar in shape, again deriving from the angles. For example, in the Himalayan monastery all the parts—stones, caps, doors, and steps—are heavily square with a line and a shallow angle. In the houses from Alberobello, all the motifs are cone-like. In the Nolli plan of

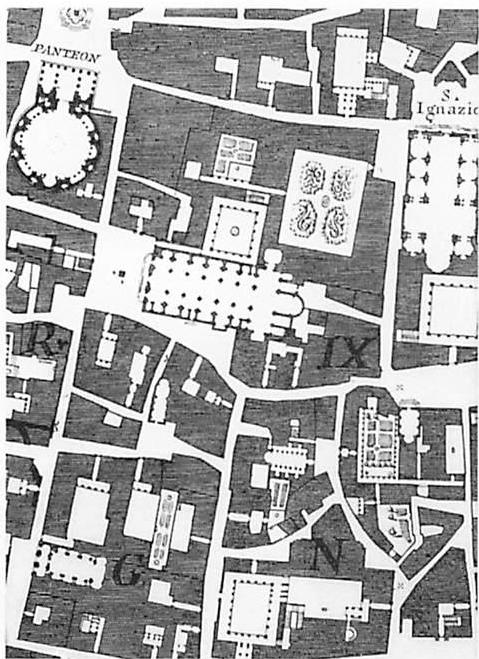
Rome, all the shapes are rectangles, or modified rectangles. However, these are only simple cases.

The more interesting cases arise when we can feel or sense a general family resemblance among a group of motifs—but the family resemblance caused by angles are deeper, and we cannot really say so easily quite why they all feel similar. In Thyangboche, the monastery in the foothills of Everest, we feel in some profound and subtle way that this building is part of the mountains: part of the Himalayas themselves. The angles of the roofs, the way the small roof sits on the larger roof, the "peak" on the largest roof, the band below the roof edge—all reflect or echo one another, and echo the structural feeling of the mountains themselves.

Even in this complicated case, it is the angles which do most of the work we feel as echoes. But it is the process which generates the building, the way stone is used, perhaps the fact that the stone is cut from those very hills and behaves the same, or perhaps because of a deep intuitive relation to the mountains that the builders had, allowing them to make something that comes from the same womb as the mountains themselves.

The essence of the echoes property lies in the very deepest level of structure. For example, in this Norwegian door, we feel the sense of echoes between all the different rectangles. The doors, the windows in the door, the panes, the panels below the windows—all have the same morphological feeling, a combination of rectangles and diamonds, and the resulting harmony between these different elements is very great. At first, we may try to identify some particular shaped rectangle as the source of these echoes—they all have a similar proportion, long and thin—and certainly there is something in this. But again there is present another deeper structural fact: that the rectangles are all bound in twos, side by side. The two panels making the door (below), the two doors, the two windows, the pairs of panes within each window—in all these cases there are two rectangles, like the leaves of an open book, and it is this two-ness in the arrangement of the rectangles which is also responsible for the sense of order. And it is this structural theme which is being echoed.

In the Norwegian barn door design made up of diamonds and circles and brackets, where

the sense of echo is very strong indeed, we may at first wonder what there is in common between diamonds and circles. But the significant fact is that the circles are arranged in diamonds, and that each circle is also at the center of a diamond-shaped space between four diamonds—the brackets embody the shape of the circle and the hint of the diamond in the space at the end, and

these four brackets are again arranged to form a diamond—this is where the echo lies, where the deepest structural relationships exist. They do not exist merely in superficial similarities among the shapes. Often this becomes most pronounced in functional or practical cases where the similar structural geometry derives from deep similarities of process that have created it.7

FUNCTIONAL NOTES

A practical example: In a well-made old barn, all the different parts are somehow made in the same way—adzed beams and columns, pegged and mortised, so that they come from a single family. This arises from practical functional consideration. Often, when all the different details are members of a family, the task of making the building becomes simpler, the rhythm of making it faster, more economical. It can produce the necessary variety without trouble. If, on the other hand, the details are disparate, it is such an effort, mentally, to make the building at all, that there is less room for variation and invention. The result: in a building without echoes, the final adaptation of the building to its needs is often weaker.

When functions are taken seriously, there are usually various geometric rules which follow, as a result of functional conditions. These rules, applied over and over again,

will create a feeling of familiar angles, lines, shapes, not for formal reasons, but simply as a result of careful adherence to functional requirements. For instance, the buildings on a hill all tend to have a similar relation to the slope, and sun and drainage, and avalanches. As a result, the hillside full of buildings, all of them obeying these laws, will tend to have echoes in their physical forms.

If something has been made without some echoes of this type, the chances are that certain deep requirements have been ignored, and the variety of non-echoing forms will cause various functional failures.

In APL similar cases are described for entrances (FAMILY OF ENTRANCES, p. 499), columns and beams (GRADUAL STIFFENING, p. 962), windows and light (LIGHT ON TWO SIDES OF EVERY ROOM, p. 746) and owned furnishings (THINGS FROM YOUR LIFE, p. 1164).

2.13 / THE VOID

In the most profound centers which have perfect wholeness, there is at the heart a void which is like water, infinite in depth, surrounded by and contrasted with the clutter of the stuff and fabric all around it.

In the Ghiordes prayer rug shown below, this takes the form of the deep blue emptiness at the center. It connects with the infinite void, and also with the center of oneself.

We see it also in certain religious buildings — there, too, one finally comes to this center, to this central void. The altar in a church, the great empty space at the crossing of a church or mosque — it is the silence, at the heart.

To understand the quality of THE VOID clearly, a contrast between two examples is helpful once again: the plan of the mosque of Baybars in Cairo, contrasted with the plan of a

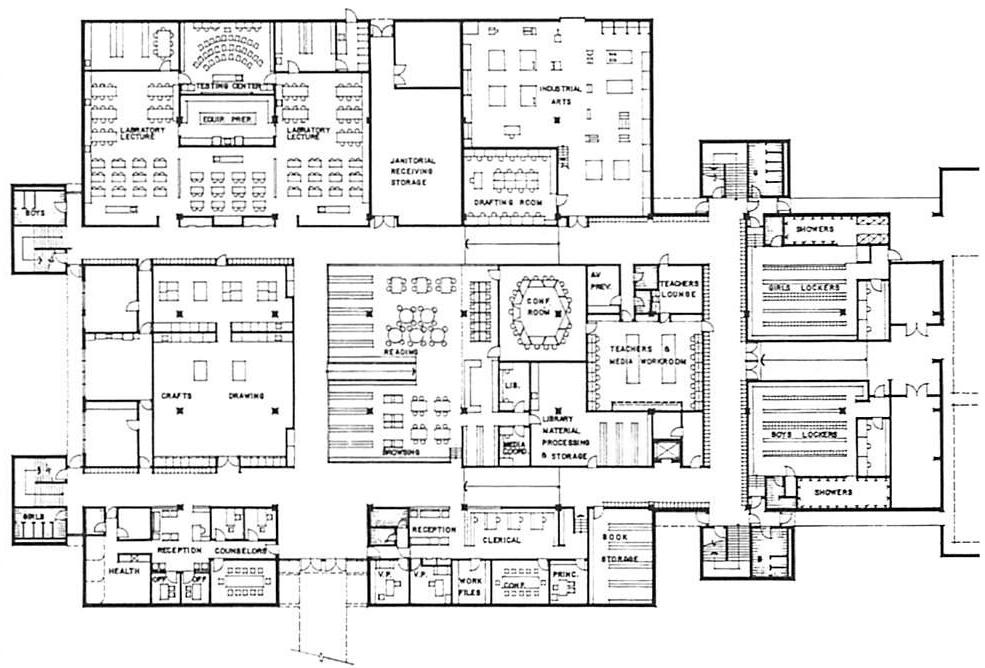
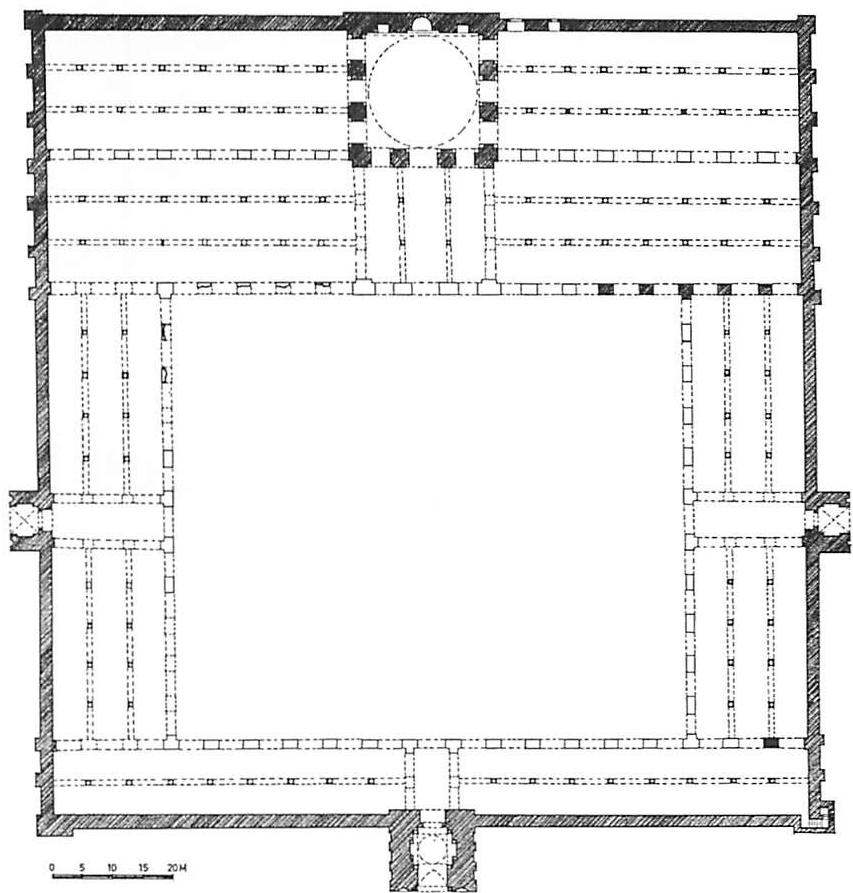
typical American office building of the 1970s. In the center of the mosque we experience the void. In the office building, there is merely an endless clutter and buzz. Nothing is still.

The difference between the two cannot be fobbed off as a difference between a religious building and an office building. When wholeness pervades, the void will be found just as clearly in the forms of workplaces. Consider, for example, a field of corn, a barn, even a duckpond in a farmyard. These are all workplaces in farm society. Each of them has the void. The cornfield is silent, concentrated in its simplicity, uncluttered because what happens there is clear. The duckpond, smaller, with weeds around the edge, has the stillness of water in the middle. Even a barn, the most practical of buildings, has a great emptiness, experienced and used, surrounded by

the structure, the braces of the building, the clutter of stored hay and farm equipment in the aisles, the stanchions and troughs along the edge.

This emptiness is needed, in some form, by every center, large or small. It is the quiet that draws the center's energy to itself, gives it the basis of its strength. The fact that the void does not exist so often now, in the buildings and objects we have in our environment, is the result of a general disturbance in our capacity to make wholeness, which is not a necessary functional property of office buildings. Most buildings today have too many small spaces in them, mixed up, scrambled — often because of a tendency to make many funky, small, "human" spaces. But there is a great lack of simple, silent, empty, large, calm space.

The need for the void arises in all centers. A cup or a bowl rests, as a living center, on the quiet of the space in the bowl itself, its stillness. A painting that is a mass of color rests on some quiet unbroken field of color, less differentiated, and concentrating the quiet to itself. In buildings, a large living room, not cramped — a large hall, not cramped — in ornaments the same. They cannot be all fuss; there must be a balance of calm and emptiness with the delirious detail. It is the way a large empty center brings life to a mass of smaller centers.

Can this be formulated as a principle of symmetry or differentiation? Is there a way that

the presence of the void arises mathematically, as part of a stable unified structure, or is it merely a psychological requirement? It is the latter. A living structure can't be all detail. The buzz finally diffuses itself, and destroys its own structure. The calm is needed to alleviate the buzz.

FUNCTIONAL NOTES

Functional examples. A large area of one material, surrounded by small amounts of another, is economical and efficient. It is much rarer to find that equal amounts of two materials will do the job.

The same rule applies in building plans. Within the buzz of smaller functions, it is always essential to have some larger spaces where a larger, slower and more calm atmosphere pervades. The failure to do this, is one of the main mistakes of modern house and building plans. One of the main things I have learned about houses — no matter how small — is that there must be a contrast of the small spaces with at least one larger space, where entirely different kinds of social and emotional things can happen.

In APL we find SACRED SITES (p. 131) which shows a great void, in the case of a mountain, or lake, as the

essence of a sacred site; ACCESS TO WATER (p. 135) which shows it for great bodies of water, and the importance of human settlement in relation to the edge of these bodies, just as the small textured centers surround the void; STILL WATER (p. 358), which requests that the water itself be made still, handled as a void. On an intimate human scale we find the same in SITTING CIRCLE (p. 857), where the circle itself, and the empty space at the heart of the circle, are small-scale manifestations of the void at work. At a similar small scale we have the tranquility of BATHING ROOM (p. 681), an example of a necessary void in the space and bustle of a household; and even SECRET PLACE (p. 930), a tiny place, hidden, somewhere in the house, yet nevertheless function in our hearts as a void, as a small zone of perfect, hidden stillness.

2.14 / SIMPLICITY AND INNER CALM

Wholeness, life, has a way of being always simple. In most cases, this simplicity shows itself in a geometrical simplicity and purity, which has a tangible geometrical form.

It is a quality—rather rare in carpets, but more common in other great works of art—which is essential to the completion of the whole. It has to do with a certain slowness, majesty, quietness, which I think of as inner calm. It is present in this Shaker cabinet, below, but is almost totally missing from the peculiar stylized Italian chairs from the 1920s.

The quality comes about when everything unnecessary is removed. All centers that are not actively supporting other centers are stripped out, cut out, excised. What is left, when boiled away, is the structure in a state of inner calm. It is essential that the great beauty and intricacy of ornament go only just far enough to bring this calm into being, and not so far that it destroys it.

As a perfect example of inner calm, I would choose Shaker furniture. What do we have in the pieces of Shaker furniture? At first sight it looks like other early American furniture. But

when we compare it with other early American furniture, we find a number of striking, and crucial, differences.

• It uses very simple shapes (the actual pieces of wood have simple shapes, and are usually close to the form in which they were first milled).
• The ornament is very sparse, but does occasionally exist to offset the classical line, with an off-curve here or there, but less than in other American pieces.
• The proportions are unusual. Pieces are unusually long, unusually high, elongated, tall, broad, etc. They are marked by their proportions as slightly unusual, or remarkable — even startling. Often this has practical good reason behind it (e.g. use all the space available).
• Many of the pieces are strange in some specific way which marks them as indeed unusual. For instance, a chest with drawers opening from different sides; two beds sliding under a bigger bed; a table with drawers hanging on either side of the pedestal; peg boards. Always these "strange" configurations have good reasons, and come from an uncompromising steadfastness to function, following the thing to its logical conclusion, refusing to be deterred by convention. An extreme freedom.
• Pieces were colored — beautiful colors, often worked into the wood (not paint), and coded, yellow, blue, red, green, etc., each type of furniture was color-coded to its function. Yet they were always severe. This severity was the very essence of the inner calm, yet so hard to pin down.
• Finally everything is still, silent.

SIMPLICITY AND INNER CALM is not only to be produced by simplicity. The Italian chairs are complex in the wrong way, and they therefore lack inner calm. The stuff which had to be cut out has not been cut away. But, for instance, the wild Norwegian dragon (on the next page) has inner calm even though it is so complex. Everything essential has been left; nothing extraneous remains. The result is simple in a profound

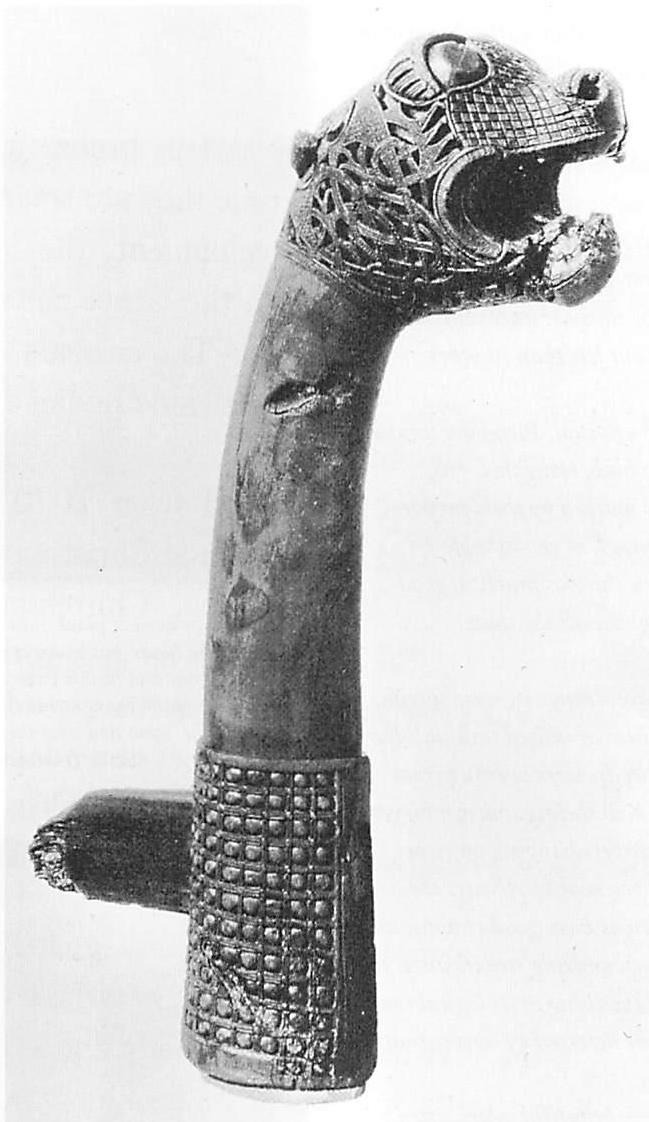
sense, but not in the superficial geometric sense. So it is not true that outward simplicity creates inner calm; it is only inner simplicity, true simplicity of heart, which creates it.

In a living whole which is correctly made, there is a special simplicity. For example, the thick low wall with a broad top is the most solid,

easiest to make, and will last the longest. When the main lines of the building are drawn simply, they will tend to give big reference to a few big things: the sun, the view, the slope. The simplicity of this response allows a deeper relationship between the person and the landscape to form; and thus creates more nourishing conditions.

FUNCTIONAL NOTES

In APL quite a number of patterns deal with this kind of ultimate simplicity of heart. They create the eye at the center of the storm, the simple core at the heart of some

part of life. Examples include GREEN STREETS (p. 266), POOLS AND STREAMS (p. 322), LOW SILL (p. 1050), SOFT INSIDE WALLS (p. 1096), and CANVAS ROOFS (p. 1128).

2.15 / NOT-SEPARATENESS

The last of these properties—ultimately perhaps the most significant—is NOT-SEPARATENESS, connectedness. What not-separateness means, quite simply, is that we experience a living whole as being at one with the world, and not separate from it—according to its degree of wholeness.

One of the most beautiful cases of not-separateness that I can point to is the 7th century Tower of the Wild Goose (shown in color on

page 11). It is so simple, so harmonious, it melts into its surroundings humbly, connects with its surroundings, is indistinguishable from its surroundings. But it does this altogether without giving up its character or personality.

At the opposite extreme, when a thing lacks life, is not whole, we experience it as being separate from the world and from itself. It stands out. An extreme of separateness—the most disastrous failure of this property—is shown in the house on this page. This house is utterly isolated. It is intended to stand out. And it does stand out as an awkward triumph of egocentricity. It fails, thoroughly, to be not-separate.

Let me summarize in structural terms what this property is all about. It states that any center which has deep life is connected, in feeling, to what surrounds it, and is not cut off, isolated, or separated. In a center which is deeply coherent there is a lack of separation—instead a profound connection—between that center and the other centers which surround it, so that the

various centers melt into one another and become inseparable. It is that quality which comes about from each center, to the degree it is connected to the whole world.

This is, finally, perhaps the most important property of all. In my experiments with shapes and buildings, I have discovered that the other fourteen ways in which centers come to life will make a center which is compact, beautiful, determined, subtle—but which, without this fifteenth property, can still often somehow be strangely separate, cut off from what lies around it, lonely, awkward in its loneliness, too brittle, too sharp, perhaps too well delineated—above all, too egocentric, because it shouts, "Look at me, look at me, look how beautiful I am."

Those unusual things which have the power to heal, the depth and inner light of real wholeness, are never like this. They are never separate, always connected. With them, usually, you cannot really tell where one thing breaks off and the next begins, because the thing is smokily drawn

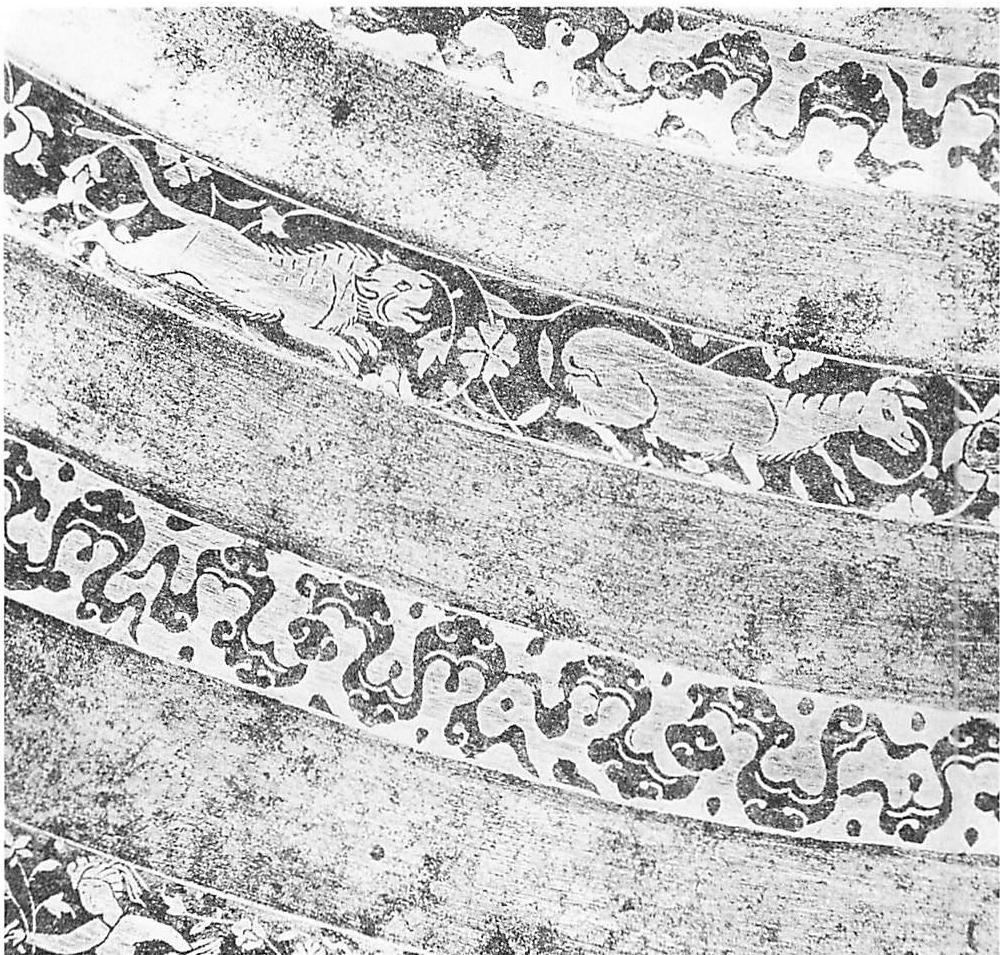
into the world around it, and softly draws this world into itself. It connects. It asserts the continuity of space, the continuity of all of us, the wisps of morning fog which hang dreaming, over the fields of flowers, like the dreaming spires of Oxford over the valley of the Thames.

This property comes about, above all, from an attitude. If you believe that the thing you are making is self-sufficient, if you are trying to show how clever you are, to make something that asserts its beauty, you will fall into the error of losing, failing, not-separateness. The correct connection to the world will only be made if you are

conscious, willing, that the thing you make be indistinguishable from its surroundings; that, truly, you cannot tell where one ends and the next begins, and you do not even want to be able to do so.

The sophisticated version of this rule, which comes about when we apply the rule recursively to its own products, produces an atmosphere like gentle evening smoke, which ties the whole together inside itself, which never allows one part to be too proud, to stand out too sharp against the next, but assures that each part melts into its neighbors, just as the whole melts into its neighbors, too. This is where the golden colors

help, where joining lines and echoes help preserve the wholeness of the thing, prevent it from disintegrating under its own inner tensions.

The structural feature which is perhaps most responsible for the easy, healed feeling of not-separateness is lack of abruptness, of sharpness. A thing which has this quality feels completely at peace because it is so deeply connected to the world around it. This quality, geometrically, depends especially on the state of the boundary. In things which have not-separateness, there is often a fragmented boundary, an incomplete edge, which destroys the hard line. Many of the most beautiful old carpets also have an infinite pattern which is randomly interrupted, as if by a window, which

also destroys the sense of self-containment of the design. Often, too, there is a gradient at the boundary, a soft edge caused by a gradient in which scale decreases (hare-and-tortoise-like) so that at the edge it seems to melt indiscernibly into the next thing—this is why things get smaller at the edge—it destroys the hard edge. Finally, the actual boundary is sometimes rather careless, deliberately placed to avoid any simple complete sharp cutting off of the thing from its surroundings—a randomness in the actual boundary line which allows the thing to be connected to the world.

The painting of the lake by Gauguin, and the paving stones in the Japanese garden, are high examples of this quality attained.

FUNCTIONAL NOTES

For a variety of functional reasons environmental systems are made more whole, and have more life, when there is a pervasive connectivity connecting the inside of the systems with other systems beyond them or outside them, making an unbroken fabric in the world. This subject is treated troughout APL, with examples from many different scales.

At the regional and urban and social scale this connectivity as a vital social matter is dealt with, for instance, in SCATTERED WORK (p. 51), OLD PEOPLE EVERYWHERE (p. 215), and SELF-GOVERNING WORKSHOPS AND OFFICES (p. 398).

It is dealt with as a physical theme in the construction of buildings, next to each other, touching each other (CONNECTED BUILDINGS, p. 531), interlocking with indoor and outdoor space (BUILDING THOROUGHFARE, p. 492, OUTDOOR ROOM, p. 163). and with the car (CAR CONNECTION, p. 553).

It is equally dealt with as a social theme in the small scale structure of buildings and neighborhoods as for instance in CONNECTED PLAY (p. 341), and SLEEPING IN PUBLIC (p. 457).

It appears as a subtle psychological matter in FILTERED LIGHT (p. 1105) and WINDOWS WHICH OPEN WIDE (p. 1100) where the subtle connection between inside and outside is specified.

Practical and ecological reasons also suggest we must try to make transitions of materials around the edge of a building, so that each material is next to something else that it can live with: for example, wood to concrete; concrete to earth. The series of transitions avoids any abrupt juxtapositions that would not hold up over time. Another example occurs in the way that terraces and paths are connected to the earth. They work best, and are most wholesome, when the connection between the stones, the paving, and the soft earth itself is so gradual, so definite, that you can hardly feel it. By comparison, a terrace which is built on stilts, up in the air, gives you access to sun and air but denies a connection to the earth. These topics are discussed extensively in CONNECTION TO THE EARTH (p. 785), RAISED FLOWERS (p. 1132), and PAVING WITH CRACKS BETWEEN THE STONES (p. 1138). The not-separateness allows the garden, and the path, and the edge of the building, and the building wall, to support each other functionally, by allowing mutual access in the right amounts to encourage necessary practical interactions.

3 / THE NATURE AND MEANING OF THE FIFTEEN PROPERTIES

Together, the fifteen properties identify the character of living systems. The regions of space which can have this living character vary enormously. If we have a bowl, a picture, a building, a forest, a pathway in a temple, a bay window in a London house — and we see all fifteen properties repeating throughout again and again and again, there is a good chance we have a thing or place whose life is profound. Systems in space which have these fifteen properties to a strong degree will be alive, and the more these properties are present, the more the systems which contain them will tend to be alive.

These include most examples of natural living systems: a clump of grasses in a swamp. They may include a medieval illuminated miniature; the window in the wonderful room at the Topkapi palace in Istanbul. They will also include, at a lower level, places or things which have more ordinary life. This may include the terrace outside your favorite gas station, a beer garden outside the Oetztal station in Austria. It may include the seaweed in a tidal flat, even with a few cans and bottles lying there.

If we look at things which have a few of the fifteen properties, less densely packed, and not all of them, we often still get some sort of living character, for instance, the stadium at Wrigley Field, a pair of roller skates, a toothbrush.

The things and systems in the world which are most dead—the most image-laden buildings and artifacts, the most sterile housing projects, the most damaged ecological systems, the most poisoned streams—will have these properties to the least degree.

Thus, although these properties define a vast family of possible places and objects and systems, all the members of this family have life in some degree. The properties, taken together, define a rough but graspable family of all those systems and things which have a great deal of life. Systems and things which lack the properties tend to be things with very little life. Thus, roughly (and I must emphasize that this is only true to a first approximation), the fifteen properties define the enormous family of systems, among all possible systems, which have life in them.

The fact that it is possible to characterize this family at all is surprising. The family which is so defined is very complex morphologically. Superficially, the many examples in this chapter look dissimilar. Each belongs to its own time and place. They vary in culture, climate, and technology. But more deeply, there is a sense in which these different cases all look the same. They all have the same deep quality; one sees the same structure, again and again, throughout the examples.

Thus we have a grip, perhaps for the first time, on the actual physical and geometrical character which living systems have. It is not too much to say that any building which has life in it, must be a recognizable member of this family. Any doorknob which has life, any window, any garden, any garden path, which has life in it, must be a recognizable member of this family.

It should be observed that this fact is not neutral with regard to theories of architecture. One cannot help noticing that the buildings of recent decades (1940–90) are noticeably missing in these properties. I believe that this is intentional, and that various unusual 20th-century theories of architecture have led architects and designers consciously to move away from these properties in the effort to promulgate some particular style or intention. For people who have been brainwashed by these recent theories of design, it may be uncomfortable to confront the factual nature of the fifteen properties. I believe this cannot be helped.

It is useful, I think, to make some mention of the dates of manufacture of the artifacts shown as examples. Readers and students have observed that many of these properties belong to ancient artifacts. They ask me, Why don't you give more examples of recently built buildings to illustrate these properties? The sad truth is that the works of the last fifty years have consciously abandoned understanding, or use, of these properties. Such works obviously do not serve well as illustrations except in a bad sense. This does not mean that

the fifteen properties have anything to do with ancient things as opposed to modern ones. Many of the examples (positive and negative) are made in the 20th century. Overall, the dates of objects range from about 1500 B.C. to A.D. 1997—a span of some 3,500 years. There is a more or less homogeneous distribution of examples over that very long period. The fact that there are relatively fewer examples to be shown from the last seventy years is not polemical, but merely factual and proportioned.

4 / THE INTERPLAY OF THE PROPERTIES

I first identified these fifteen properties during the years 1966–73. By 1976 they were well defined, and it was clear to me that they occurred repeatedly in those artifacts which have life. Somewhat later it became clear, too, that these properties also occur repeatedly throughout nearly all of nature (see chapter 6).

However, in 1976, it was not yet clear to me how to interpret these properties. They were, at that time, only raw products of observation. I knew that these features appeared repeatedly both in great buildings and works of art, and in nature, but I had no clear idea what they meant, or where they came from.

In addition, there was a puzzle caused by the relationship of the properties to one another. The fifteen properties are not independent. They overlap. In many cases we need one of them to understand the definition of another one. For example, if we try to define ALTERNATING REPETITION exactly, we need to get clear that there is an alternation between certain things or STRONG CENTERS which repeat. These "things" are discernible wholes only because they have a definite shape. Thus the definition of alternating repetition relies heavily on the GOOD SHAPE of the things that are repeating—and on the good shape of the things between the things that are repeating. Similarly the definition also relies on

the POSITIVE SPACE between the things which repeat, and on the CONTRAST between the two systems of things which are repeating.

The same thing happens when we try to define LEVELS OF SCALE. The different levels are not discernible at all, until we identify the things at different levels as wholes: that is, unless we assume we know what it means for the centers at every level to be STRONG CENTERS and have GOOD SHAPE. The levels of scale property also doesn't work unless some of the elements are big and open, as required by THE VOID. And the hierarchy of levels relies strongly on the fact that the things at lower levels repeat, and sometimes alternate, in their repetition.

GOOD SHAPE is a shape which contains powerful centers within the BOUNDARIES of the shape. ALTERNATING REPETITION succeeds when the space between the alternating entities is POSITIVE SPACE. Centers often become more powerful when they are bounded by BOUNDARIES themselves made of STRONG CENTERS.

The same thing happens for every one of the fifteen properties. The more carefully we think about each property, and try to define it exactly, the more we find out that each property is partly defined in terms of the other fifteen properties. Although the fifteen properties seem distinct at first, they are in fact intertwined and interwoven.

The matrix below gives a rough overview of the way the properties are interdependent. When I first identified the fifteen properties this pattern of interdependence seemed very puzzling and troublesome. It meant that the properties are not "atomic" or fully independent features of systems. However, I soon began to think this was significant and important rather than troublesome. The interdependence of the properties seemed to contain a hint of something else, something richer and more complex than the properties themselves—and also more unitary—which somehow lay behind the properties. I began to realize that these fifteen properties were indicators, rough approximations of some deeper structure which looked and felt like "all of them together."

This "deeper" structure had to be an extended thing in space, a "something" which ex

isted across space, and which allowed the fifteen properties to emerge from it. During the late seventies, I began thinking that this "something" must be some kind of field in which centers create wholeness and wholeness intensifies centers.

I finally recognized that it is the field of centers which is primary, not these fifteen properties, and that the properties are simply aspects of the field which help us to understand concretely how the field works.

At that stage I began to formulate the basis for a new view of space based on wholeness, in which these fifteen properties appear naturally and inevitably from the nature of wholeness, and in which it becomes clear how and why life occurs in space, not as an attribute of living organisms, but as an attribute of space itself.

THE INTERACTIONS OF THE FIFTEEN PROPERTIES
If property A depends on property B or we need property B for a complete understanding of property A then an asterisk appears in cell AB
		PROPERTY B
		LEVELS OF SCALE	STRONG CENTERS	BOUNDARIES	ALTERNATING REPETITION	POSITIVE SPACE	GOOD SHAPE	LOCAL SYMMETRIES	DEEP INTERLOCK AND AMBIGUITY	CONTRAST	GRADIENTS	ROUGHNESS	ECHOES	THE VOID
PROPERTY A	LEVELS OF SCALE
	STRONG CENTERS
	BOUNDARIES
	ALTERNATING REPETITION
	POSITIVE SPACE
	GOOD SHAPE
	LOCAL SYMMETRIES
	DEEP INTERLOCK AND AMBIGUITY
	CONTRAST
	GRADIENTS
	ROUGHNESS
	ECHOES
	THE VOID
	SIMPLICITY AND INNER CALM
	NOT SEPARATENESS

5 / HOW THE FIFTEEN PROPERTIES HELP CENTERS COME TO LIFE

Let me therefore now go over, once again, the specific individual roles of the fifteen properties. Having observed the properties, having noticed them, it is important to ask exactly what they are, and to understand them more deeply, in relation to the structure of wholeness, and the structure of centers. Simply put, I believe that these properties arise because they are the principal ways in which centers can be strengthened by other centers. They are, if you like, fifteen ways of talking about centers, and the way that the existence and life of centers dominates the existence of life in the world.

1. LEVELS OF SCALE is the way that a strong center is made stronger partly by smaller strong centers contained in it, and partly by its larger strong centers which contain it.

2. STRONG CENTERS defines the way that a strong center requires a special field-like effect, created by other centers, as the primary source of its strength.

3. BOUNDARIES is the way in which the field-like effect of a center is strengthened by the creation of a ring-like center, made of smaller centers which surround and intensify the first. The boundary also unites the center with the centers beyond it, thus strengthening it further.

4. ALTERNATING REPETITION is the way in which centers are strengthened when they repeat, by the insertion of other centers between the repeating ones.

5. POSITIVE SPACE is the way that a given center must draw its strength, in part, from the strength of other centers immediately adjacent to it in space.

6. GOOD SHAPE is the way that the strength of a given center depends on its actual shape, and the way this effect requires that even the shape, its boundary, and the space around it are made up of strong centers.

7. LOCAL SYMMETRIES is the way that the intensity of a given center is increased by the extent to which other smaller centers which it contains are themselves arranged in locally symmetrical groups.

8. DEEP INTERLOCK AND AMBIGUITY is the way in which the intensity of a given center can be increased when it is attached to nearby strong centers, through a third set of strong centers that ambiguously belong to both.

9. CONTRAST is the way that a center is strengthened by the sharpness of the distinction between its character and the character of surrounding centers.

10. GRADIENTS is the way in which a center is strengthened by a graded series of different-sized centers which then "point" to the new center and intensify its field effect.

11. ROUGHNESS is the way that the field effect of a given center draws its strength, necessarily, from irregularities in the sizes, shapes and arrangements of other nearby centers.

12. ECHOES is the way that the strength of a given center depends on similarities of angle and orientation and systems of centers forming characteristic angles thus forming larger centers, among the centers it contains.

13. THE VOID is the way that the intensity of every center depends on the existence of a still place—an empty center—somewhere in its field.

14. SIMPLICITY AND INNER CALM is the way the strength of a center depends on its simplicity—on the process of reducing the number of different centers which exist in it, while increasing the strength of these centers to make them weigh more.

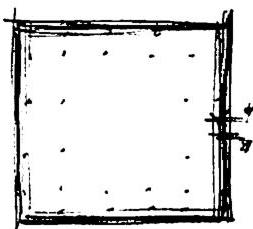
15. NOT-SEPARATENESS is the way the life and strength of a center depends on the extent to which that center is merged smoothly—sometimes even indistinguishably—with the centers that form its surroundings.

The fifteen properties are not independent. They overlap. In many cases we need one of them to understand the definition of another one. This is because it is the field of centers itself which is primary, not these fifteen properties. The properties are simply aspects of the field which help us to understand concretely how the field works.

However, even though the properties do not have primary significance and it is the field of centers, or the wholeness itself, which is primary, still there is an important sense in which the fifteen ways may represent an exhaustive description of all possible ways in which the field of centers works. Each of the properties describes one of the possible ways in which centers can intensify each other. Each one defines one type of spatial relationship between two or more centers, and then shows how the mutual intensification works in the framework of this relationship.

In effect, the fifteen properties are the glue, through which space is able to be unified. The fifteen properties provide the ways that centers can intensify each other. Through the intensity of centers, space becomes coherent. As it becomes coherent, it becomes alive. The fifteen properties are the "ways" it comes to life.9

Are there any other ways? Is this catalogue of fifteen merely a random sample of the possible ways in which centers can produce a field? Or is this an exhaustive and complete list?

The number fifteen is only rough. At various stages in the evolution of this theory, I have

had a catalog of twelve, fourteen, thirteen, fifteen, sixteen. The precise number fifteen is not significant. But I do believe that the order of magnitude of the number is significant. Throughout my efforts to define these properties, it was always clear that there were not five, and not a hundred, but about fifteen of these properties. It wasn't possible to go on listing new ones indefinitely.

There is no certainty that this list is exhaustive. On the other hand, if you try to think up other effects which are combinatorially different from these, you will find it is not very easy. When we focus on the mathematical ways in which centers can be built out of other centers, or the ways in which one center helps to make other centers stronger, there is a limit to the number of ways in which this can be done.

NOTES

1. These properties may be thought of as an elaboration of the observations, recorded more informally in THE TIMELESS WAY OF BUILDING (New York: Oxford University Press, 1979), chapter 23. It was the content of that chapter, written in 1975, which stirred in me the need to start the observations that are recorded here.

2. Christopher Alexander and Susan Carey, "Sub-symmetries," PERCEPTION AND PSYCHOPHYSICS 4 (1968): 2, 73–77; Christopher Alexander and Bill Huggins, "On Changing the Way People See," PERCEPTUAL AND MOTOR SKILLS 19 (1964): 235–53. The experiments are also discussed further in appendix 2.

3. Toward the end of Book 2 (chapter 14), we shall see that almost everything about life in buildings can, in the end, be understood through symmetries, and that, indeed, there may be a way in which the concept of wholeness, and the field of centers, when understood dynamically, can be understood completely in terms of a sequential unfolding of symmetries.

4. Evidently there is a deep connection between the presence of local symmetries in a field and the occurrence of a center. In empirical studies of wholeness symmetry has always played a role. Symmetry is one of the powerful ways that space is made whole. When a part of space is symmetrical it is internally coherent.

5. For the case of a crystal, Humphries argues that there is more structure in the grid with slight irregularities, because it still has the grid structure, but some additional differentiations and other structures as well. Humphries in ASPECTS OF FORM, ed. L. L. Whyte 1951 (Bloomington, Indiana University Press, 1961).

6. Soetsu Yanagi, THE UNKNOWN CRAFTSMAN (Tokyo: Kodansha International Ltd, 1972).

7. In physics and biology, "homology."

8. See chapter 4.

9. It is vital for the reader to understand that, even though they are so important, the fifteen properties are not essential in themselves. What matters in the end is the life of the centers. The importance of the properties is simply that they help you to understand the way that centers come to life. I often give students the task of making small drawings in which they illustrate the fifteen properties one by one. When a student does this, there are two kinds of things that can happen. In one case, A, the property is present in the drawing so that, formally, one may say that the property exists there. But in the case A, nothing really happens. Life does not enter the drawing because the student has not really understood the meaning of the property. Life and feeling are not increased: so the essential inner meaning of the property has not been understood.

In another case, B, the student uses the property in such a way that because of it the drawing gets more life. Thus the property is useful, active, powerful, in helping to bring life and feeling into that drawing. In this case, B, I say that the student has understood the property.

What is the real difference between these two cases, A and B? It hinges on the fact that a drawing gets life when the centers in the drawing have life; when there are many living centers, instead of a few only; and when the centers have a deep intensity of life in them. So, in a drawing which has life and feeling, it has it because the centers in it are alive. What all this means is that the property itself is not important. What is important is only the fact that centers must be created, densely, and that they must be given life.

That is what I mean by saying that, really, the properties are not so important, and can be "thrown away"—and that what really matters is the person's ability to see the centers, to make more and more centers, and to make them come to life. But I do not want to undervalue the properties. It takes years—perhaps three, five, ten years—to learn the process of making centers, and to know what it means to make a center come to life. In the meantime, the properties are a very useful tool; they are a way of focusing our attention on the centers. By following the properties, even if blindly, like a mechanical tool, we gradually come to know more and more and more about the life of centers—we appreciate the way that centers interact, we learn to make the life of one center more intense, by adding, or providing other centers—and the property thus teaches us, concretely, more and more about how we can make centers come to life. That is the whole ball game in the end.

CHAPTER SIX: THE FIFTEEN PROPERTIES IN NATURE

1 / INTRODUCTION

The fifteen properties are not merely visual features which appear in works of art. According to the theory put forward in chapters 3 and 4, these properties must be viewed as fundamental to the existence of the wholeness in the world, wherever it exists. They must, therefore, be fundamental to the appearance of life in all centers that are generated or created in any system.

If this is true, the properties would be fundamental to all physical structures of any kind at all and must be expected to appear not only in successful artifacts but in nature, too.

In this chapter, I shall show that the fifteen properties do indeed appear at many scales throughout the natural world. It is important for the reader to understand that this is a significant and rather surprising result, not merely a casual observation. Although it is easy enough to see that the properties do appear in many natural systems, none of the present-day theories of natural systems explains why these properties appear so widely. The explanation of their appearance in nature will require powerful new dynamic methods of analysis that are defined in Book 2.

2 / BEYOND COGNITION

If we are to use the theory of centers — and the concept of life — as the basis of all architecture, it would be reassuring to know that wholeness, together with the properties which bring centers to life, is a necessary feature of material reality, not merely a psychological aspect of things which arises during perception of works of art.

In the previous chapters, we have seen how wholeness and its field of centers illuminate our understanding of buildings, paintings, bowls, columns, seats, and carvings. We have seen abundant physical evidence that this wholeness exists in the world of buildings and artifacts, and that their quality depends on the system of centers, and especially on the degree of life the individual centers give each other. The more pronounced this field of centers is — the more intense the centers, the more connected, and the more dense they are — the more life there is in the thing.

A skeptical reader could, however, make relatively light of these claims. According to a "cognitive" interpretation, the centers could merely exist in the mind's eye (as products of cognition), and the fifteen properties, which apparently make the

centers work, could also exist merely as artifacts of cognition. According to such an interpretation, it might be said that buildings and works of art look good when they are made of centers in the way I have described, simply because they correspond somehow to deep cognitive structures — that is, to the way human perception and cognition work. In this interpretation, these explanations would be a powerful way of understanding the psychology of buildings and works of art — and would tell us something important and significant about visual phenomena in the world. But they would not have implications beyond the psychological — certainly not for the way the material world actually works. By themselves, they would certainly not support my claim that this new view of architecture is necessarily linked to a new view of space and matter and to the fundamentals of the way the world is made.

Now, to suggest the unity in which atoms, rivers, buildings, statues, trees, paintings, mountains, windows, and lakes are all part of one unbroken system, I shall argue that nature too is understandable in terms of wholeness, and must

be understood this way. I shall try to show that the structure of centers I call the wholeness goes deeper than mere cognition, is linked to the functional and practical behavior of the natural world, not only the architectural world, and is as much at the foundation of physics and biology as it is of architecture. This will, later, give new insights into the character of nature, how the unfolding of the wholeness which occurs in nature is responsible for the character of natural structures — and how, finally, the unfolding of wholeness might one day be understood as a single law which underlies the entirety of everything we know as nature.

3 / APPEARANCE OF THE FIFTEEN PROPERTIES IN NATURE

Centers, wholes, and boundaries occur repeatedly throughout the natural world. For example, the water in the river is never perfectly homogeneous. There are variations of temperature, depth, velocity, concentration of chemical ions, and so on. If these variations did not exist, then we would not be able to distinguish any special zones in the river. But in practice, we distinguish definite kinds of places in the river: the fast-flowing stream, the slow-moving edges, the warmer upper layer, the relatively colder depths, the sunny areas, the muddy shallow parts, and so on. We recognize these distinct parts not merely because they are relatively more homogeneous but because the differentiation and homogeneity have structural and ecological consequences. The fast-moving stream in the middle is the place where fish, animals, boats move quickly. The slow-moving edge nourishes plant life and encourages animal habitats. The cold water at the bottom is better for various kinds of fish. The mud at the bottom is the right place for worms, larvae, fish debris.¹ Each of these zones attracts different secondary and tertiary conditions and finally becomes established as a “system.” Thus the differentiated, non-homogeneous zones gradually develop with their own properties, and their own unique kinds of action, events, organisms, and behavior.

This is entirely typical. Similar differentiations occur in the sun, in a fire, in a desert, in a chemical “soup,” in a growing crystal, in a developing embryo, even in interstellar space. It is simply part of the way the world is made that the non-homogeneity of space leads to progressive differentiations, which then allow different kinds of systems and boundaries to develop. The zones where conditions are relatively more constant tend to be identified as zones of a single “type.” Then, by contrast with these zones, the transition areas between them tend to become boundary zones.

This kind of differentiation, which occurs continually throughout the physical world, is not a matter of our perception. It is real physical organization, which manifests itself in the world and has functional consequences in the behavior of the systems. For example, if we look at a leaf, we see the harder parts of the leaf where ribs occur and the fleshier parts between. This is not merely a perceptual distinction, but a real distinction between two types of components in the nature and behavior of the leaf. The harder spinier ribs deal with structural forces, and the softer fleshier parts allow photosynthesis to occur. If we break a leaf in such a way as to maintain the integrity of these wholes, the leaf is more likely to survive than if we rupture the leaf across these systems, thus destroying the integrity of the wholes.

Further, the wholeness or integrity of each subsystem creates a center. When a cell, which has a nucleus and an outer boundary zone, acts as a center within the organism, it becomes stronger than either the boundary zone or the cell nucleus by itself. It becomes mechanically

more coherent as a result of its role in the larger system. Here we see a "mechanical" counterpart of the strength of centers which we have seen cognitively in chapter 5.

In general, the "strength" of any center — its degree of life — is a measure of its organization. One might measure this by its lifetime as a structure, or by its ability to resist disruption, or by its influence on the wholes around it. By almost any of these measures, the stronger a center is, the more powerful its impact on other nearby centers, and the more it will influence the behavior, motion, coagulation, organization, and reorganization of the other centers which come under its influence. Thus the system of powerful centers in the world has a practical and immediate physical influence on the behavior of other nearby centers.

The relationships of different nearby centers follow the same scheme we have already seen. Again and again, the fifteen properties appear as geometric features of the way that space is organized in nature, and of the way the centers that appear in space are distributed.

4.1 / LEVELS OF SCALE

Why does the electrical discharge in the photograph opposite have levels of scale in it? The massive build-up of charge dissipates in a rush, leaving zones which have a remaining charge that are by definition much smaller than the original charge. These small zones discharge, once again leaving still smaller ones, which then discharge in a kind of mopping-up operation. The levels of scale follow naturally from the way this system brings itself to order.²

In related fashion, the appearance of levels of scale is widespread throughout natural systems. The tree: trunk, limbs, branches, twigs. The cell: cell wall, organelles, nucleus, chromosomes. A river: bends in the river, tributaries, eddies, pools at the edge. A mountain range: highest mountains, individual peaks, surrounding foothills, still smaller sub-hills. Limestone: large particles, smaller particles, smallest particles each in the interstices of larger ones. The sun and solar system: planets and their orbits, satellites and their orbits. A molecule: component complexes, individual atoms and ions, neutrons, protons, electrons. A flower: individual flower heads, center and petals, sepals, stamens, pistils.

In general terms, it is not hard to see that in any system where there is good functional order it is necessary that there be functional coherence at different levels, hence necessary that there are recognizable hierarchies in the organization of these functional systems. The presence of a continuous range of structures, at different scales, with one level never too far from the next level above or below, is common both in organic and inorganic nature. For instance, a tree has a trunk, limbs, branches, and twigs to carry the load of the leaves and to distribute sap. There is a hierarchy because a limb of any one size can serve only a comparable volume and cannot therefore reach each part of this volume, except by breaking down into smaller elements, which can, more economically, reach smaller volumes of the tree. In the case of formation of galaxies, stars, solar systems, planets, and satellites, it seems that, in the overall process of gravitational condensation, there is always a residue, a level of structure not accounted for by the forces at one level, which then condenses, usually under the impact of a slightly different pattern of forces, to produce yet another level of structure in the hierarchy. In the same way, a molecule is made up of component complexes, which contain individual atoms and ions, which themselves contain neutrons, protons, and electrons. These fundamental particles are themselves

made up in some way from the combination and recombination of the underlying quarks. In this case, the explanation goes the other way: each small element, of whatever size, is

sufficiently complex, so that by the time there are two or three, or ten of them, the geometry of the combination is complex enough to produce entirely new kinds of forces, which therefore exhibit new kinds of behavior, and so gain existence as coherent semistable entities at a higher level. The phenomenon of levels is so pervasive in nature that it even occurs within the physics of the human cognitive system itself, as a feature of information processing and memory.[2]

Few natural systems lack the structure of levels because, in nature, scale plays such an important role. When we double or triple the size of a given thing, there are already different forces at work, a different interplay of phenomena, and therefore new kinds of wholes are born, for purely physical reasons. Thus, at the next scale larger than cells, in a plant, there are aggregations of cells which obey different laws and start to form new wholes—the aggregations themselves form larger aggregations, again with new laws—and each new level comes into being as soon as the order of magnitude of the phenomenon is changed.

However, it is extremely difficult to formulate a theory which explains the general phenomenon, and the general existence of levels of scale in almost all naturally occurring systems. Attempts have been made, for instance by L. L. Whyte, Albert Wilson, and Donna Wilson, by Cyril Smith, and by Michael Woldenberg. But, to my knowledge, no general mathematical explanation has been given which predicts the formation of these levels or the size of jumps between levels. Particular theories deal only with particular cases of level-formation, not with the formation of levels in general. And indeed, there is no easily defined form of mathematics within which the emergence of such a phenomenon might be predicted. Bifurcation theory might give a possible clue by identifying natural breakpoints in development of a system. But, to my knowledge, it has not yet been attempted. Explained or not, the property itself is pervasive throughout nature.

4.2 / STRONG CENTERS

Why does the splashing milk drop form such a perfect center as it splashes, almost like a medieval crown? I shall not be able to give the full answer to this question until Book 2.⁶ But we can see, in part, what happens. First, the falling drop has radial symmetry: as it hits, the milk splashes out almost equally in all directions. But why does a little drop form at the end of each ray, almost as if the structure were a crown, and so that these small

drops then intensify the center of the main ring that has been formed?

We certainly see strong centers throughout the physical world. Many natural processes have centers of action. The action, or development, or force-field radiates outward from some system of centers. This is implicit in much of physics and biology. In physics, we have the fact that electric, magnetic, gravitational, and nuclear

forces are carried by spatially symmetrical fields, thus most often creating centrally and bilaterally symmetrical structures. In biology, the most familiar case of centrally driven order is the development of an embryo, where nodes known as "organizers" serve as sources of chemical fields, the fields formed by concentrations of different endocrine substances which control growth.7 The centers formed by these nodes play the major role in the organization of the embryo's growth. We see the residue of these growth centers in the actual hierarchy of centers in the adult organism. Field-like systems of centers appear also in fluid flow, hydrodynamics, pressure systems, and electrostatics, and have been proposed for particle dynamics also.8 Among the best-known, very large-scale cases are the thread-like centers that appear in the interaction of plasma with magnetic fields to create galaxies, galactic systems, stars, and planets.9 Similar but less complex processes occur in many other non-organic systems and, of course, in the pervasive system of centers which occurs in a molecule, formed by nuclei and electron orbits.10

However, as in the case of levels of scale, it is very hard to give a general explanation of the widespread occurrence of centers and center-based phenomena. We observe the fact of their existence in a wide range of phenomena, but have no general mathematical theory which fully explains it.

4.3 / BOUNDARIES

In nature, we see many systems with powerful, thick boundaries. The thick boundaries evolve as a result of the need for functional separations and transitions between different systems. They occur essentially because wherever two very different phenomena interact, there is also a “zone of interaction” which is a thing in itself, as important as the things which it separates.

Consider the surface of the sun: there is a zone there, many thousands of miles deep, where the flames of the sun’s inner fire shoot out into space. This is where the near vacuum of space interacts with the inner nuclear reactions of the sun’s interior, an interaction so peculiar, in its own right, that it occupies a massive volume.

Or, at a very different scale indeed, consider the wall of an organic cell, a massively thick structure where all the flow in and out of the cell is controlled. The cell wall is as thick, almost, as the interior of the cell itself.[11] Or consider the banks of a river: the zone between the actual dynamics of the flowing river itself and the fields or countryside which surround it. Here again, there is a massive boundary, an area of shallow water, a muddy edge, with its own specific animals and plants, its own quite definite ecology, formed once again by the fact that this zone has its own laws, its own necessary structure. In the case of the Mississippi River, the high-velocity stream flow carries mud and silt out into the Gulf of Mexico, depositing the boundary material of

the "banks" so far out into the gulf that the river's boundaries are visible from the air, almost one hundred miles out to sea. The photograph shows a similar phenomenon where the Rio Negro flows into the Amazon.

As in these examples, it is widespread in many other natural systems that the boundary between two phenomena, instead of being merely a dimensionless interface, is itself a solid zone with its own distinct coherent properties and shape. Thus, for instance, the wall of a cell is as thick as its entire diameter because a great deal of chemical structure is needed to control exchanges between its interior and exterior. The

wall of a lung is an imbricated boundary structure where all the actual "work" of the lung occurs, where oxygen is absorbed by the hemoglobin and placed into the bloodstream, and later carboxyhemoglobin is broken down so that its carbon dioxide can be released. The outer layer of an atom—its electron shells—is far larger than the nucleus, and it is precisely in this outer layer that connection and interaction occur as the atoms combine to form molecules.

Although each of these cases is understandable in its own terms, the difficulty of providing a general explanation of the appearance of boundaries is considerable.

4.4 / ALTERNATING REPETITION

Recall the distinction, made in chapter 5, between simple repetition and alternating repetition. In nature most of the repetitions which occur are alternating rather than simple. Repetition itself of course occurs simply because there are only a limited number of archetypal forms available, and the same ones repeat over and over again, whenever the same conditions occur. Atoms repeat in a crystal lattice; waves on the surface of water repeat; cloud forms repeat in cirrus; mountains in a mountain range repeat; so do

the trees in a forest, leaves on a tree, atoms in a crystal, cracks in a piece of dried-up mud, petals on a flower, flowers on a bush.

In most of these cases of natural repetition, the repeating units do alternate with a second structure, which also repeats. When atoms repeat, so do the spaces which contain the electron orbits; when waves repeat, so do the troughs between the waves; as mountains repeat, so do the valleys; when the trees in a forest repeat, so do the open patches of undergrowth where more

light falls; when leaves repeat, so do the spaces between the leaves that allow the sun to reach the leaves; when cracks in mud repeat, so do the coherent and harder units of the uncracked mud between them; when petals in a flower repeat, so do the sepals which lie behind the petals and overlap them; when the flowers on a bush repeat, so does the space between the flowers; when the tiger's stripes repeat, so do the lighter stripes between them.

Some of these cases (like waves and troughs) are so obvious that they almost seem tautologous—as if the second repeating structure cannot help being there—not for physical but for logical reasons. But that is not so. In all these cases, the significant issue is the coherence of the secondary centers. The defining feature

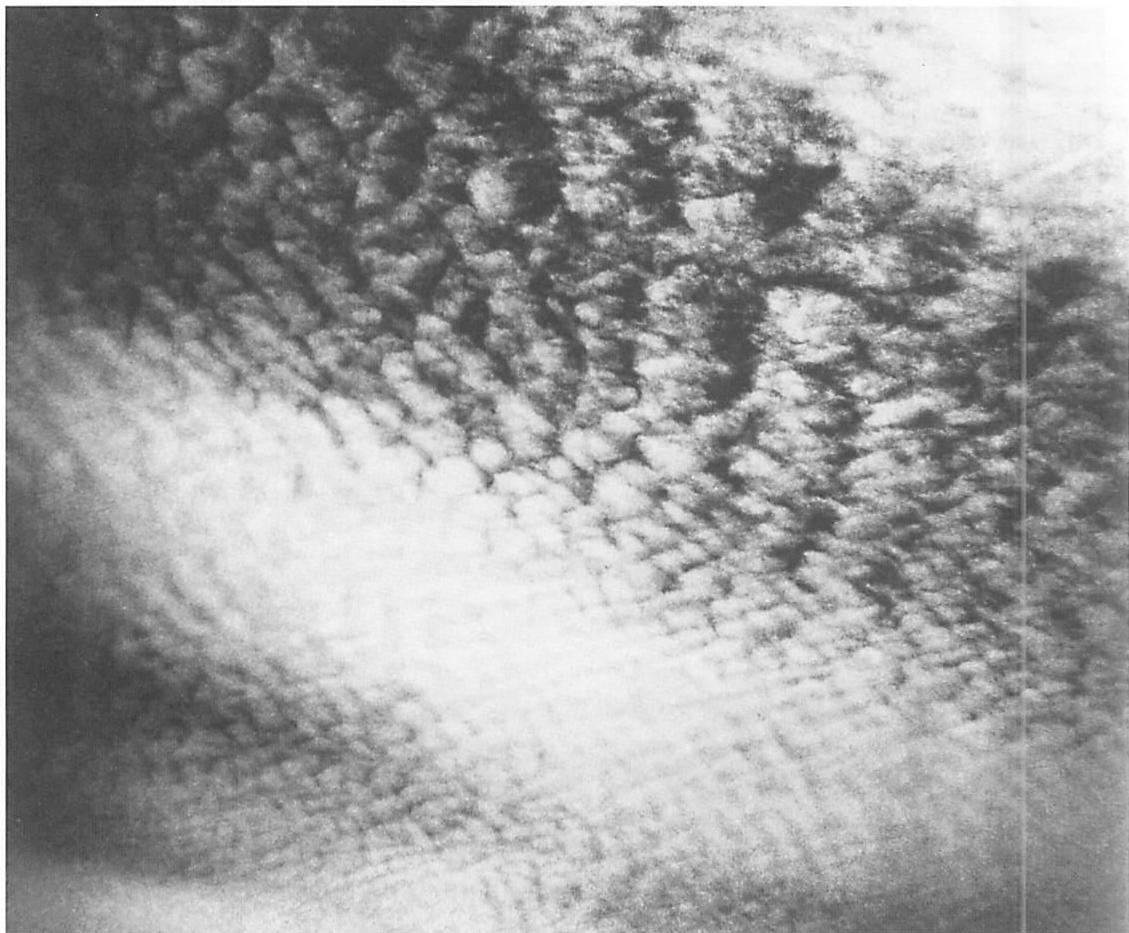
for ALTERNATING REPETITION lies in the fact that the secondary centers are coherent in their own right, are not left over. This happens in most natural systems because the secondary centers occur as coherent systems in themselves, with their own laws, their own defining processes and stability.

It is also significant that the physical size of the secondary alternating units is very often at the same order of magnitude as the size of the primary repeating units. In the mackerel cloud formation seen above, why is it that the size of the space between the white parts is about the same as the white parts themselves? The dynam-

ics of vapor formation create clouds of a certain size. The nucleation of the vapor in this clump "sweeps" another volume clean of vapor. The space loses its vapor as the denser droplets form in the adjacent zone. As the cloud forms, the space full of vapor and the spaces emptied of vapor alternate and form the striated pattern we see in the sky.

As the examples make clear, we see the appearance of this phenomenon in a plethora of forms throughout nature. In particular cases, its occurrence is certainly not a mystery. Yet no simple theory that I know of explains or predicts its pervasiveness.

4.5 / POSITIVE SPACE

In a great variety of natural systems, we find something very much akin to the positive space I have described in chapter 5. In the majority of naturally developed wholes, the wholes and spaces between wholes form an unbroken continuum. This arises because the wholes form "from the inside" according to their specific functional organization, thus making each whole positive in its own terms. The positive nature of the space is necessary to preserve the wholeness of the system.

For example (next page), each bubble in a cluster of soap bubbles presses outward; as a result of this equilibrium the bubble walls flatten out, and the space inside the bubbles becomes

positive. In the second example illustrated on the next page, of ink flowing in gelatin, the river of ink has its own laws and its own pressure, as does the gelatin. The same thing happens with the crystals which take on coherent polyhedral shapes as they butt into each other while they grow. Unlike a single crystal, which may form non-positive space next to it, each bit of space is occupied by an outward thrusting crystal, making all the space positive.

In the crazing of porcelain (below), we see a similar effect. As the surface cools, the glaze shrinks, forming cracks. The areas bounded by cracks are coherent in shape because

the cracks follow maximum stress lines and form in such a way as to relieve maximum stress. As a result, the areas bounded by the cracks all turn out to have good shape, more or less compact, and all about the same size. The energy of the crazing equalizes out, and ensures that they are all positive.

In all these cases, the positiveness of the space—what we might also call the convexity

and compactness of the centers which form—is the outward manifestation of internal coherence in the physical system. Thus we have an intuitive idea of why it keeps happening. It is difficult, however, to formulate in terms which can be established as a general rule, because, without the language of living centers, it is not clear how the idea of positive space could be formulated accurately.

4.6 / GOOD SHAPE

A great many natural systems have a tendency to form closed, beautifully shaped figures: leaves, the curl of a breaking wave, a cowrie shell or a nautilus, a harebell, a bone or a skull, a whirlpool, a volcano, the arch of a waterfall, the hooves of a horse, the outline of a moth or a butterfly, the Chladni figures produced by a violin bow vibrating a steel plate with sand on it — all have natural and beautiful shape.

In order to understand the widespread occurrence of beauty of these shapes in nature, we must remember that a GOOD SHAPE is a geometric figure — often curved — which has in it some major center that is intensified by various minor centers. If we look carefully at the

Chladni figure, we notice that the curves of which it is made have a definite and noticeable peculiarity. This comes from the fact that each curve surrounds one center, then surrounds another center on its opposite side, then back again. The particular character of the curve comes from the double system of centers which exists inside the curve formed by the stationary nodes of the vibration. In each case, the fact that an intense major center is surrounded by various intense minor centers is directly connected with the physical behavior of the system. The special shape of the sycamore leaf, with its full curves and reverse-curves at the tips, comes from the relative rates of growth of different parts of the

perimeter. Again, the good shape arises because each part—the inside of the full curve, and the sharp point of the tip—exists as a center, which is developed very fully in the growth process.[12] In the electron orbitals inside a molecule, for similar reasons, we see similar curved surfaces, with their own three-dimensional version of good shape caused by the interaction of the curves in space.

The appearance of good shape in nature has been noted informally by many writers, notably by D'Arcy Wentworth Thompson.[13] I believe however, that a general explanation of this widespread appearance of good shape in nature has not yet been formulated, chiefly because the concept of good shape has not yet been expressed in precise language. Once again, without the concept of a living center, it is hard to see how this could be formulated precisely.

4.7 / LOCAL SYMMETRIES

Local symmetries are pervasive throughout nature. The sun is symmetrical (roughly), a volcano is symmetrical around its center, trees are symmetrical around their trunks, crystals are symmetrical, the human body is symmetrical in its major bilateral symmetry and in many of its individual parts (a finger around its length, an eye, a fingernail, a woman's breast, a knee).¹⁴ Rivers are roughly symmetrical about their line of flow; so, approximately, is a spider's web, and so are the leaves on the tree—even the veins which lie within the surface of the leaf are more

or less symmetrical. Plants are often roughly symmetrical, both in their totality and, more finely, in details like their leaves. And, of course, local symmetry also occurs in simpler phenomena. For instance, when a star forms, it creates a rotating sphere which is symmetrical around its axis. A drop of water is approximately symmetrical about the vertical axis; a free-floating soap bubble is symmetrical. A ray of light, being a straight line, is symmetrical about its own axis and from end to end. Molecules often have one or more axes of symmetry.¹⁵

In general these symmetries occur in nature because there is no reason for asymmetry; an asymmetry only occurs when it is forced. Thus, for instance, a water drop, falling through the air, is asymmetrical along its length, because the flow-field is differentiated in the direction of fall, but symmetrical around its vertical axis, because there is no differentiation between any one horizontal direction and any other. In short, things tend to be "equal" unless there are particular forces making them unequal.

In addition, the existence of local symmetries in nature corresponds to the existence of minimum energy and least-action principles. A soap bubble is symmetrical because the symmetrical sphere is the shape which minimizes the

Surface structure of aluminum: here we see many local symmetries, not only on the fully formed crystals, but in the partially formed crystals which have started to grow. Each zone of growth establishes its own local symmetry.

potential energy due to surface tension. The crystal is symmetrical because the continuous aggregation of equal particles usually leads to an array which, for geometric reasons, has global symmetry.[16]

In the majority of these cases, it is also the presence of layer upon layer of subsymmetry at smaller scales which is important. A Rorschach blot is symmetrical as a whole, but possesses no significant symmetries at lower scales. This kind of form, random at lower levels but symmetrical in the large, is relatively uncommon in nature. Contrast it with snow crystals which display symmetries at many levels. They are symmetrical in the large, but the smaller symmetries, nested within the whole, give them their structure. Each branch is repeated six times, on the six arms of the hexagon. Each one of the six arms is bilaterally symmetrical along its length. And

the smaller shoots, which branch off from the main arms at 60 degrees, are again symmetrical within themselves. It is this multiple, multilayered symmetry that convinces us of the "structure" in the snow crystal.

The appearance of symmetry in nature is possibly the most widely noticed of the fifteen properties. It has been written about by a multitude of writers. And local symmetries, particularly, were discussed by Alan Turing, in his essay on morphogenesis.[17] Later work on symmetry breaking has also begun to explain in general how local symmetries form, and propagate, in a wide variety of general physical systems.[18] So in the case of this property, we do have the beginnings of a general theory which predicts that locally symmetric structures and nested symmetries will arise, in general, throughout the range of natural systems.

4.8 / DEEP INTERLOCK AND AMBIGUITY

Deep interlock comes about in many natural systems because neighboring systems interact most easily along extended or enlarged surfaces, where the surface area is large compared with the volume.

A well-known example exists at the surface of the cerebellum. In order to increase the surface area, and thus permit the maximum number of connections with surrounding tissue, the cerebellum is crinkled deeply. The magnetic domain in a ferrous crystal has a similar structure: two domains, deeply interpenetrated, allow two materials to be in contact for an enormous surface area within a constant volume.

Ambiguity, a similar phenomenon, comes about when a subsystem belongs simultaneously to two different overlapping larger systems. One of the most important and dramatic examples of

this kind of overlap exists in the case of molecules. Simply put, the molecule is given its structure by the overlap of the electrons in the outer electron shells of the component atoms. What is important for our purposes is the following: the stability of the molecule (or the binding energy of the bond) is determined by the depth of overlap or interpenetration of the electron shells. A table published by Bernard Pullman shows how the deeper the interpenetration and overlap, the more stable the molecule.¹⁹

A general theory to explain the pervasiveness of deep interlock and ambiguity might be formulated in terms of surface area and the impact of reactions and interactions between systems. Although it would be hard to do this in numerical terms which are fully general, it might be done in qualitative terms.

4.9 / CONTRAST

Many—perhaps all—natural systems obtain their organization and energy from the interaction of opposites. We see this at a fundamental level in the following chart of elementary particles, which contains particles and antiparticles, positive and negative electric charges, charmed and anti-charmed quarks, up and down quarks, and anti-up and anti-down quarks.

On a biological level, we see it in the contrast of male and female which exists in almost every kind of organism. It appears in the cycle of day and night, formed by a rotating earth in sunlight. It appears in the contrast of solid and liquid phase which provides the action and catalysis in chemical reactions. More informally it exists in the contrast of dark and light in the surface of a butterfly, which attracts the mate.

As in other properties, the obviousness of the way that contrast works in particular cases is nevertheless hard to explain or predict as a

general rule. It would be extremely hard to show, from first principles, why contrast must arise, necessarily, as a property of any naturally occurring system, and one wonders whether the matter is not merely cognitive. We read contrast; our cognition depends on it; therefore we think it is important. And yet the fundamental contrast of dark and light, positive and negative, can hardly be an artifact of our cognition.

The nearest thing I know to a general explanation of its appearance in the world is the one given by Spencer Brown. His beautiful account of all mathematics arising from the contrast (distinction) between nothing and something tries to show how all structure and form, at the most elementary level, come from contrast.[20] But why the systems in which living structure appears seem to have contrast more strongly than others—that remains a mystery.

4.10 / GRADIENTS

Gradients play a very large role throughout nature. Any time that a quantity varies systematically, through space, a gradient is established. For instance, as we climb on a mountain, the higher we go, the climate becomes colder, and the air becomes thinner. In these gradually changing conditions, trees become more thinly spaced, finally giving way to grass and then to rocks, and then to rocks and ice.

In an electric field, the field-strength varies with distance from the charge, forming a gradient of intensity. In a growing plant or embryo,

chemical gradients induced by concentrations of different growth hormones, control emerging cell division and cell type, thus forming morphological gradients in the growing organism.

In a river, we have gradients of turbulence and velocity near the river bank; we have a gradient in the size of drops as we go around the curl of a breaking wave; we have a gradient of sizes visible toward the edge of almost any phenomenon. An organism grows as a result of a field of chemical hormones which vary in concentration outward from some central point. The size of

twigs varies in a gradient-like way, outward from the center of a tree; the ice crystals in a zone of varying temperature exhibit a gradient.²¹

The idea of regular gradient-like variation is fundamental to the whole integral and differential calculus, and it is the fact that these mathematical tools are closely mirrored in many phenomena of nature that is essentially responsible for the success mathematical physics has had. The gradients of an electromagnetic field, of a hydrodynamic field, of a gravitational field are the tools, first made available by tensor calculus, which have given us such powerful analyses for a vast array of phenomena in physics.

Even so, there is little of a general nature in complex system theory that explains why those living structures that are stable among rocks, plants, and animals have graded variation in such pervasive and accentuated form.

4.11 / ROUGHNESS

Roughness, or irregularity, appears pervasively in natural systems. It appears as a result of the interplay between well-defined order and the constraints of three-dimensional space.

The kernels in a corn cob, for example, are all bead-like; but when squashed, each takes on a slightly different shape as it adapts itself to the complex configuration of the cob. The waves of

the sea are all very similar, but each wave is different according to variations in wind, speed, and configuration of nearby wave systems. The peas in a pod are all approximately spherical but vary in size according to the boat-shape of the pod; the line of a twig is roughly straight but gnarled by the places where still smaller twigs break in; the slope of a mountain is often roughly

uniform but is interrupted by areas of greater slope where rocks occur and by flatter places where water has made it level.

Even a very regular thing like a crystal is interrupted by the irregularities we know as dislocations because small increments of error make it impossible to continue the exact periodicity and grid structure forever. Crystal dislocations are now understood to be a necessary feature of ordinary crystal growth.[22] An irregular world

struggling to be regular always achieves a certain level of regularity which is interrupted by unusual configurations created by the very forces that produce the regularity as they act against a framework of three-dimensional constraints inherent in space.

An excellent example of roughness in nature is visible in the radiolarian, illustrated by Hermann Weyl. This animal's outer shell is a sphere made of a mesh of hexagons. However, a well-known theorem of Leonhard Euler's proves that a sphere cannot be covered with a mesh of hexagons, since the number of sides and vertices do not add up right.[23] So, for a reason which has to do with the nature of space itself, the radiolarian must have a few cells with fewer than six sides—and indeed, in the actual creature, we see that about five percent of the cells are pentagons. This illustrates vividly how the quality of roughness, far from being caused by inaccuracy or "sloppiness," instead occurs where there is a partial misfit between a very well-defined order and the space or configuration where it occurs.

This forces an apparent irregularity, not for its own sake but to create a greater regularity.

We see the same thing, less vividly, in the markings and coats of animals. The stripes of a zebra come about simply from the interaction of a regular generative process with a complex surface: the outer skin of the animal. If we were to try and paint stripes on a horse with perfect regularity, they would not fit at all, and we should have something that looked, and was, far less regular, far less orderly than the zebra's coat. Once again, the apparent irregularity arises from the system's attempt to be as orderly as possible.²⁴

It is fascinating that even atoms, for so long virtual archetypes of perfect repetition, are now known to vary, each from the next, according to the subtle electronic orbits and boundary conditions causing interactions. This is physically visible in photographs recently showing—for the first time—individual atoms in their individual shapes within a crystal. Within the regular array, each atom is slightly different according to its

position.²⁵ To my knowledge, there has not yet been a general account of roughness as a necessary feature of a morphological system in which minute adaptations are occurring.

4.12 / ECHOES

In all natural systems, deep-lying fundamental processes ultimately give geometric form to the static structure of the system. These processes repeat certain typical angles and proportions over and over again, and it is the statistical character of these angles and proportions which de

termines the morphological character of the system and its parts—even within parts which seem superficially different. For example, an aging man's face has a certain craggy character which appears in his nose, eyebrows, cheeks, stubble, and chin. The same process of skin tightening,

sagging, and weathering repeats similar combinations of angles over and over again. It is this which gives the beautiful consistent character of the different areas in the man's face.

The lily has its characteristic curves and the same delicate proportions formed by similar growth processes in each different component. As a result, its stems, lips of the petal, stamens, all have the same proportions and the same combinations of angles, and we feel the echoes in the system. The similarity of character—the echo—is a result of key parameters in the growth rules. One example published by Peter

Stevens, a detailed study of sap flow in trees, shows why a given species of tree always has a similar system of branching angles as a result of least energy expended in relation to the sap viscosity.[26]

If we wanted to give a general theory, we might say that echoes appear in nature because uniform growth processes create natural homomorphisms and isomorphisms among the different parts of any single system. However, a precise theory explaining the appearance of echoes in natural systems has yet to be formulated.

4.13 / THE VOID

The void corresponds to the fact that differentiation of minor systems almost always occurs in relation to the "quiet" of some larger and more stable system.

Thus smaller structures tend to appear around the edge of larger and more homogeneous structures. In plasma physics, for example, this appears in the form of systems of galaxies which have strongly homogeneous zones,

bounded by more intricate zones where the structure is more intense and more densely distributed.[27]

A hint of something that might one day be a general theory showing why the void will occur in complex systems to maintain their wholeness, appears in the most general models of fractal geometry.[28] Beyond that we have little explanation.

An example of simplicity and inner calm: a lone tree in the Sahara, a tiny oasis against the endless sand, shows that the persistence of the void as a feature of living structure may not be easy to explain. A detailed complex structure appears here against the counterpoint of a vast repeating simplicity. Why does this feature recur?

4.14 / SIMPLICITY AND INNER CALM

Simplicity and inner calm is the Occam's razor of any natural system: each configuration occurring in nature is the simplest one consistent with its conditions.

For example, Michel's theorem shows that the typical three-dimensional form of a leaf, with the particular way the plan and cross-section vary from stem to tip, is the least-weight structure for a cantilever supporting a uniformly distributed load. Thus, the natural form of a leaf closely approaches the "ideal," least-weight, and simplest form.[29] The surface of a boiling fluid takes the shape which has least energy per unit mass. Many naturally occurring forms are given by minimum principles of this kind.[30]

Why nature follows these minimum energy principles is, surprisingly, not entirely clear.

However, the principle of least action, discussed at some length in Book 2, chapter 1, provides a rather ancient formulation of simplicity and efficiency which approximates the condition in a highly general way.

4.15 / NOT-SEPARATENESS

Not-separateness corresponds to the fact that there is no perfect isolation of any system, and that each part of every system is always part of the larger systems in the world around it and is connected to them deeply in its behavior.

This deep interconnectedness of all things is visible in science and in the quantum mechanics of the late 20th century has been openly talked about. However, there is very little actual scientific research which directly deals with it. For examples of theory which even touch on this matter, one must go far afield and stretch small bits of theory, metaphorically, to extend them to domains where they have not yet concretely appeared.

An early formulation of a similar general intuition was given in the Mach's principle which asserts that all particles of matter are somehow deeply connected so that gravity itself, and the

gravitational constant $G$ , are dependent on the total amount of matter in the world, and thus are somehow directly linked to every other particle of matter.[31]

In terms of current theory, this intuition could be understood as related to the principle known as Bell's theorem, which asserts a deep connectedness in the fabric of matter and space so fundamental that it appears that parts of the world are linked even without the transfer of normal mechanical or causal processes.[32]

This property and the previous two properties (the void and simplicity and inner calm) are so complex that, at our present state of mathematical knowledge, there is almost no possibility that they might be formulated in precise language, or that one could give a general theory of why these phenomena occur that is more than poetic.

5 / WHY DO THE FIFTEEN PROPERTIES OCCUR IN NATURE?

From the examples in this chapter, we see that the fifteen properties appear again and again throughout nature. They occur and recur at every scale—in subatomic particles, atoms, crystals, organisms, rocks, mountains, forests, global phenomena, and large-scale water and weather systems. They appear in plants, streams, clouds, animals, flowers, valleys, and rivers. In effect, they appear throughout nature—apparently because of the normal evolution of systems.

Virtually always, the specific structure of centers in a given case can be explained as a result of forces and processes which are mechanical in the conventional sense. For example, a mountain has a certain slope which keeps repeating because at any steeper angle the material simply falls off, thus creating echoes in the slopes and rocks and hillocks of the mountain's shape. A drop of water has a flattened, nearly spherical good shape, because the surface tension of the drop pulls it into a minimum surface area for its volume, and forces of wind friction, gravity, and elasticity slightly modify the sphere.

However, such mechanical explanations do not explain why the properties themselves keep showing up. The properties appear over a wide range of scales. They certainly appear at the scale of "everyday" (that is, at the scale of our own human bodies). They also appear equally at microscopic and subatomic scales, and at astronomical and cosmological scales. In short, these geometric properties occur commonly, throughout nature, at all scales. Yet, in spite of that, as I have said, it is not usually possible to give a general explanation, or general theory, which explains why a particular property occurs pervasively as a repeating feature of the natural world.

Let me illustrate this argument in more detail. Consider the example of boundaries. Why do "large" or "fat" boundaries appear repeatedly in different kinds of systems? The reason that a human blood cell has a thick boundary is that

it "needs" a processing zone, where inputs to the cell are filtered and distributed before reaching the nucleus. On the other hand, the reason that the Rio Tapajós has an immense boundary where it enters the water of the Amazon is simply that the silt deposits which come down the river are hurled out into the water of the larger river, creating a chain of islands along both sides of the stream, for nearly one hundred miles. And the reason that the sun has a thick boundary—the corona—is different again. There is a temperature gradient from the hot interior of the sun to the cold of outer space. The relatively cooler transition zone between these two zones takes up an enormous volume of space, hundreds of thousands of miles deep, which gives rise to physical phenomena of plasma, flames, and radiation quite unlike those in the sun's interior. So, a big boundary does in fact appear in all three cases—but the reasons for the existence of the fat boundary are entirely different in each.

Can it be a coincidence? That is hardly credible. It does not seem possible to dismiss the

appearance of thick boundaries as meaningless or as a coincidence. One guesses that there must be some higher-order explanation for the repeated formation of the boundary property. And, more generally, one guesses that there must be a higher-order explanation, too, for the repeated appearance in nature of all the fifteen properties.

What might these explanations be? We have learned, in chapter 5, that the fifteen properties are fifteen different ways in which centers in the world can intensify each other and form larger centers.

One wonders, then, if there might be a more general language for talking about function than the one we are used to—a language which talks only about the most fundamental connections and relations between systems and is based on centers. In such a language, the properties might be explained, reasonably, as the structural complements to the formation of stable and semistable systems. Just as I have suggested, in chapter 5, that the fifteen properties are the ways in which centers can sustain each other's coherence, so this might apply equally to those functional wholes in nature which appear within any stable or semistable system. They would then be the fifteen

major ways in which "sustaining" between subwholes of a system does actually take place.

From this point of view, consider again the boundary property of the sun. The corona is a zone several hundreds of thousands of miles deep, occupying an intermediate zone between the very hot interior of the sun where thermonuclear fusion is taking place and the cold reaches of outer space beyond the sun. In this intermediate boundary zone, certain specific reactions take place, which form a magnetic container for the sun's plasma, and which are needed to maintain the equilibrium of the whole system. We see then that in this case, the integrity or wholeness of the boundary layer plays a vital role in helping to maintain the integrity of the sun's interior.

In different fashion, the boundary of a cell's nucleus also plays a vital role in maintaining the wholeness and stability of the living cell. And the boundary of the Río Tapajós's stream flow and the silt deposits in the Amazon are a natural result of the way the river flows. They, too, serve to separate the flow of the river in the Tapajós from the dynamically and ecologically different water of the Amazon.

Of course, none of these possible arguments explain why natural processes tend to create stable systems in the world. (This matter is taken up in Book 2.²³) But I do observe, for the present, that, for whatever reason, boundaries contribute to the stability and coherence of natural systems. For similar system-reasons — so my argument goes — the other fourteen properties, too, will tend to appear in almost any natural system which is functionally stable or semistable, contributing in some way to its coherence and stability. Each of the fifteen properties does something of a characteristic nature to maintain the integrity and viability of natural systems. The appearance of these properties is linked to the stability and robustness, of the world.

That is because these properties represent the most fundamental ways in which space can be molded to form character, to create form, to form unique structure that is capable of having properties, behavior, and interesting or useful interactions with other structures.

We might say that it is the fifteen properties which are responsible for the robust and practical character of nature, the very fact that the world works, that things happen, that matter has behavior. The fact that storms blow, that cows can be milked, that streams run on mountains, that rocks form, that trees fall over or are consumed by fire, that the earth regenerates in spring, that earthquakes come, that buildings rock and shake and then sometimes withstand the shaking, that birds perch in the tree and snakes move in the grass, that human community is present in the ecology of a neighborhood — all this, what I call the robustness of the earth, comes directly from the fifteen properties. It arises because of the character of natural stuff as living structure, endowed with centers which support each other, and which make each other more alive. All this that we recognize as the normal stable character of nature comes from its robustness — from an evolving morphology which works.

6 / THE CONCEPT OF LIVING STRUCTURE

If the foregoing arguments are correct, the repeated appearance of the fifteen properties in natural systems is a profound result, not merely a by-product of presently available mechanical explanations about the world.²⁴ Rather, it suggests a new view of all nature as living structure. It implies that the scheme of things I began to define in chapters 1 to 5 — the distinction between degrees of life in things, the role played by the fifteen properties in creating life in space — is not merely appropriate for artifacts, but must be extended to include all naturally occurring structures. In this scheme of things, nature itself then becomes visible as something quite different from the mechanical nature that 19th- and 20th-century physicists used to imagine.

Let us go back to the issue of life defined earlier. In chapters 1 to 5, I introduced the idea that the structures I am trying to characterize are structures which have life. In nature, these structures appear in a wide variety of systems and phenomena — indeed, in virtually all structures, and not only in those of an organic nature (where there is literally biological life) but in all natural structures. In some sense the same morphological character occurs in mountains, rivers, ocean waves, blown sand, galaxies, thunderstorms, lightning, and so forth. There is life — more of it and less of it — in inanimate nature, too.

But all this — all of what we loosely and traditionally call “nature” — is then characterized by just that actual life which I have identified in the better human artifacts. Within the terms of my definitions, then, nature as a whole — all of it — is made of living structure. Its forests, waterfalls, the Sahara desert and its

sand dunes, the vortices in streams, the ice crystals, the icebergs, the oceans, all of it—inorganic as well as organic—has thousands of versions of living structure. Whether organic or inorganic, most of it is alive in the terms that I have defined. The living character of these structures is different from the character of other conceivable structures that could arise, and it is this character which we may call the living character of nature.

When we think it through, there appears to be a puzzling anomaly in this conclusion. Among natural phenomena, the fifteen properties seem to appear, pervasively, in almost everything. Yet among human artifacts, the fifteen properties appear only in the good ones. How can the very same properties be marks of good structure in human artifacts, and yet be present in all of nature? What is it about nature which always makes its structures "good"?

The essence of the problem is that we have not, as far as I know, ever yet concentrated our attention on the fact that in nature, all the configurations that do occur belong to a relatively small subset of all the configurations that could possibly occur. It is that which permits, I believe, the characterization of a certain class of structures as living structure.

To make this more clear, consider two mathematical sets of possible configurations. First, is the domain $C$ , which contains all possible three dimensional arrangements that might exist. It is almost unimaginably large, but nevertheless (in principle) it is a finite set of possible configurations. Second is the domain $L$ , of all configurations which have living structure as I have defined it. $L$ , too, is very large, but smaller than $C$ . Just how large depends on the cutoff for structures we include as being living.

These two sets, $C$ and $L$ , are rather artificial. My definitions have not been precise enough to make them perfectly welldefined. Still, naming them is useful, because it allows me to say something important, that I could not say otherwise. The essence of my point is simple. It may well be that all naturally occurring configurations lie in

The domain $C$ , of all possible configurations; and the domains $L$ , of living structure. $L_{1}, L_{2}, L_{3} \ldots L_{n}$ are shown as smaller and smaller domains, reflecting progressively greater degrees of life with correspondingly smaller numbers of possible configurations.

$L$ while, on the other hand, not all man-made configurations lie in $L$ .

For this to be true, we merely need to show that for some reason nature, when left to its own devices, generates configurations in $L$ , but that human beings are able, for some reason, to jump outside $L$ , into the larger part of $C$ . That is, human beings—and designers, above all—are able to be un-natural.

The sum total of all that could occur $(C)$ , is the set of all possible (imaginary and actual) configurations that might appear in the world. But nature does not create all possible configurations. In fact, what we call nature only creates things from a drastically limited set of configurations $(L)$ , which are constrained by restrictions on the types of process that occur in nature. Essentially, nature always follows the rule that each wholeness which comes into being preserves the structure of the previous wholeness, so that all of nature is just that structure which can be created by a smooth structure-preserving process of unfolding.[35]

That is why we see the fifteen properties throughout almost all of nature, at almost all scales.[36] And, even though this living structure in nature is a product of natural laws, in buildings and human artifacts, which are works of imagination, these restrictions on structure-preserving processes do not necessarily apply. It is possible—very easily possible—for human designers to design unnatural structures of a kind which could not (in principle) occur in nature.

In nature the principle of unfolding wholeness (to be described in Book 2) creates living structure nearly all the time. Human designers, who are not constrained by this unfolding, can violate the wholeness if they wish to, and can therefore create non-living structure as often as they choose.

The important thing to recognize is that nature — all nature — is a living structure. This, on reflection, must lead to insights and modifications in our idea of what nature is and how it works.

8 / A NEW VIEW OF NATURE

The concept of wholeness as a structure depends on the idea that different centers have different degrees of life, and therefore on the idea that the existence of these varying degrees of life throughout space is a fact about the world. To say that every part of nature has its wholeness, is to say that we cannot look at nature correctly without seeing distinctions of degree of life — and hence of value — within nature itself.

If we consider one part of nature — the interplanetary space between Jupiter and Saturn, for example — we cannot help being impressed by the relatively featureless character of this space. Even if this space has important minor variations in it, it is relatively featureless when compared with the structure of a rock, or a birch tree, or a meadow. The articulation and complexity of the field of centers is less developed in the interplanetary space.

The traditional scientific view has been that, in spite of this obvious difference between more complex and less complex space, still, as scientists we should be committed to a view where each of these structures — the empty space, the rock, the plant — are “equal” in value.

A world-view based on the existence of wholeness comes out rather different. If the field of centers is a governing structure which underlies all physical reality, then there is a crucial objective sense in which there is less value in the empty space, somewhat more value in the rock, and still more value in the birch tree.

In this objective sense, the relative degree of value, or relative degree of life, in different parts of matter, must then be a fundamental and objective feature of reality. Not all nature is equally beautiful. Not all of it is equally deep in its wholeness. Some of nature may be “better” than other parts of nature.

If this is true, it must provoke thought about deep problems. We must acknowledge that some places in the world are more damaged, and have a less coherent, less limpid structure. When man interferes with nature, we very easily get places where the simple and deep beautiful structure is replaced by something stark and harsh. Love Canal in New York, for instance, famous in the 1960s, was a place where chemicals destroyed the life of the water and took the place of a complex structure with hundreds of species and dozens of ecological niches. Introduction of certain chemicals destroyed this complex structure, left a toxic slime, and barely a handful of species remained. The complex structure of the water habitat had been destroyed or severely damaged.

Within the view of wholeness, and within the view that recognizes the existence of living structure, one of the most fundamental tenets of contemporary science — that value is not part of science and that all matter is, from a scientific point of view, equally value-free — can no longer be sustained. If different centers have more life and less life, more intense life, and less intense life, then material structures in which centers with more life occur — or where they occur more densely — are inherently more valuable.

This would represent a change of viewpoint. In the new viewpoint, the harmony of na-

ture is not something automatic, but something to be marvelled at — something to be treasured, sustained, harvested, cultivated, and sought actively. We are led to a new view of the natural world, different from the scientific-mechanistic view which has prevailed in recent centuries. Value, emerging as a deeper life in the wholeness of the world, turns out to be a fundamental aspect of nature itself. The variation in degrees of value occurs even among ice crystals; among the plants in a forest; in a planetary system; on a single mountain; in society; in human beings. Although much of nature is relatively neutral, beginnings of differences in value occur within nature itself.

Once people appear on the planet, the difference becomes sharply accentuated. Most human actions are governed by concepts and visions. These may be — but may easily not be — congruent with the wholeness which exists. Under the influence of concepts, it becomes harder and harder for us to remain in harmony with the emerging wholeness. Often our actions, intentionally or unintentionally, are at odds with our own wholeness, and at odds with the wholeness of the world. The gradual emergence of value is then drastically threatened. The activity of building the world — what we call architecture — plays a huge part in this process. Both those parts

of the world which are still natural — such as valleys, fields, and streams — and those which are clearly man-created — such as towns, buildings, streets, gardens, and works of art — may either go towards greater value and greater wholeness, or towards greater ugliness and confusion.

In our era, this situation has become acute. We may recognize that the world is a system in which deep wholeness can occur as an objective matter of fact. But it does not necessarily occur. The activity of building—what we call architecture, and with it also the disciplines we call planning, ecology, agriculture, forestry, road building, engineering—may reach deeper levels of value by increasing wholeness, or they may break down value by destroying wholeness. This is not a stylistic observation, or a culturally induced opinion, depending on a point of view. If what I have argued is true, this is a matter of fact about the wholeness in the world. Life will increase, or it will degenerate, according to the degree in which the wholeness of the world is upheld, or damaged, by human beings and human processes.

In this situation, the task of architecture, as something which contributes or does not contribute to the overall emergence of living structure in the world, becomes a vital issue which touches all of nature.

NOTES

1. Rachel Carson, THE SEA (London: Hart-Davis, MacGibbon, 1964); Paul Colinvaux, "Lakes and Their Development as Ecosystems," INTRODUCTION TO ECOLOGY (New York: John Wiley & Sons, 1973); and J. David Allen, STREAM ECOLOGY: STRUCTURE AND FUNCTION OF RUNNING WATERS (New York: Chapman & Hall, 1995).
2. Michael J. Woldenberg, "A Structural Taxonomy of Spatial Hierarchies," COLSTON PAPERS, 22 (London: Butterworths Scientific Publishers, 1970); and Peter Stevens, PATTERNS IN NATURE (Boston: Little, Brown & Co., 1975), 108-14.
3. George A. Miller, "The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information," PSYCHOLOGICAL REVIEW 63 (1956): 81-97.
4. One symposium devoted only to this topic is L. I. Whyte, Albert G. Wilson, and Donna Wilson, eds.,

HIERARCHICAL STRUCTURES (New York: American Elsevier Publishing Company, Inc., 1969). Another author much concerned with the necessary appearance of hierarchy is Cyril Stanley Smith, A SEARCH FOR STRUCTURE: SELECTED ESSAYS OF SCIENCE, ART, AND HISTORY (Cambridge, Mass.: MIT Press, 1981). Michael J. Woldenberg, A STRUCTURAL TAXONOMY OF SPATIAL HIERARCHIES (Cambridge, Mass.: Laboratory for computer graphics and spatial analysis, Graduate School of Design, Harvard University, 1970). 5. For an account of bifurcation theory, see René Thom, STRUCTURAL STABILITY AND MORPHOGENESIS: AN OUTLINE OF A GENERAL THEORY OF MODELS trans. from French by D.H. Fowler (Reading, Mass.: The Benjamin/Cummings Publishing Company, 1975). 6. For a fuller explanation see Book 2, chapter 1, "The principle of unfolding wholeness in nature," and chapter 2, "Structure-preserving transformations."

7. For Spemann's theory of organizers, see H. Spemann, "Experimentelle Forschungen zum Determinations- und Individualitätsproblem," NATURWISSENSCHAFT 7 (1919).

8. A very long shot, that might conceivably give a general basis, is the possible use of spinors or twistors as a way of describing particle processes in terms of centers, Roger Penrose and Wolfgang Rindler, SPINORS AND SPACE-TIME (New York: Cambridge University Press, 1986).

9. Hannes Alfven, WORLDS-ANTIWORLDS: ANTI-MATTER IN COSMOLOGY (San Francisco: W.H. Freeman & Co., 1966).

10. Bernard Pullman, THE MODERN THEORY OF MOLECULAR STRUCTURE, trans. by David Antin (New York: Dover, 1962).

11. Stephen W. Hurry, THE MICROSTRUCTURE OF CELLS (London: John Murray Ltd., 1965); and THE LIVING CELL (San Francisco: W.H. Freeman and Company, 1965).

12. The idea that curves are essentially defined in their most important attributes by cusps and concavities — which means precisely by the centers formed in the curve — is developed fully by Louis Locher Ernst, EINFUEHRUNG IN DIE FREIE GEOMETRIE EBENER KURVEN (Basel: Birkhauser Verlag, 1952).

13. D'Arcy Wentworth Thompson, ON GROWTH AND FORM (Cambridge: Cambridge University Press, 1917).

14. For very nice overall discussion of symmetries in nature see Hermann Weyl, SYMMETRY (Princeton: Princeton University Press, 1952). Also see A. V. Shubnikov, N. V. Belov, and others, COLORED SYMMETRY William T. Holser, ed. (Oxford: Pergamon Press, 1964).

15. H. Jaffe and Milton Orchin, SYMMETRIE IN DER CHEMIE (Heidelberg: Dr. Alfred Huthig Verlag, 1973).

16. See, for example, Brian P. Pamplin, ed., CRYSTAL GROWTH (New York: Pergamon, 1980).

17. L. Fejes Toth, REGULAR FIGURES (New York: Macmillan, 1964); Andreas Speiser, THEORIE DER GRUPPEN VOM ENDLICHER ORDNUNG (Berlin 1958); and H. S. M. Coxeter, INTRODUCTION TO GEOMETRY (London 1961). Turing's early theory of morphogenesis includes the idea that local symmetries must develop, and will play a significant part in, the morphogenesis. A. M. Turing, "The Chemical Basis of Morphogenesis," in PHILOSOPHICAL TRANSACTIONS OF THE ROYAL SOCIETY, B (London: 1952), 237 ff.

18. See discussion in Ian Stewart and Martin Golubitsky, FEARFUL SYMMETRY: IS GOD A GEOMETER? (Oxford: Blackwell Publishers, 1992), throughout, and especially 166–68.

19. Pullman, THE MODERN THEORY OF MOLECULAR STRUCTURE.

20. Spencer Brown, LAWS OF FORM (London: Allen & Unwin, 1969), 1 ff.

21. Stevens, PATTERNS IN NATURE.

22. See for example Simon Toh, "Crystal dislocations," in INTRODUCTION TO MATERIALS SCIENCE (University of Queensland: Department of Mining, Minerals, and Materials, 2000).

23. Weyl, SYMMETRY, 89–90.

24. A detailed explanation of the formation of zebra stripes has been given as a diffusion reaction model, in James D. Murray, "How the Leopard Gets Its Spots," SCIENTIFIC AMERICAN 258, no. 3 (March 1988): 80–87. In this model the roughness, which comes about as a result of interaction between the rules of the diffusion reaction system and the surface geometry of the animal, is clearly explained as a necessity.

25. Hans von Baeyer, TAMING THE ATOM (London: Viking, 1992). The first photographs of atoms.

26. Stevens, PATTERNS IN NATURE, 94–6.

27. See, for example, Hannes Alfven, "Galactic Model of Element Formation," IEEE TRANSACTIONS IN PLASMA SCIENCE, 17 (April 1989): 259–63.

28. Benoit B. Mandelbrot, THE FRACTAL GEOMETRY OF NATURE (New York: W.H. Freeman & Co., 1983).

29. H.L. Cox, THE DESIGN OF STRUCTURES OF LEAST WEIGHT (Oxford: Pergamon Press, 1965), 105–13, and especially fig. 44.

30. For many examples of variational problems, see Stefan Hildebrandt and Anthony Tromba, MATHEMATICS AND OPTIMAL FORM (New York 1984); see also L.A. Lyusternik, SHORTEST PATHS: VARIATIONAL PROBLEMS, translated and adapted from Russian by P. Collins and Robert Brown (New York: Macmillan, 1964).

31. See, for instance, Charles Misner, Kip Thorne, and John Wheeler, GRAVITATION (San Francisco: W.H. Freeman, 1980); and Hermann Weyl, PHILOSOPHY OF MATHEMATICS AND NATURAL SCIENCE (London 1950).

32. For a non-mathematical account of Bell's theorem, see David Peat, EINSTEIN'S MOON: BELL'S THEOREM AND THE CURIOUS QUEST FOR QUANTUM REALITY (Chicago: Contemporary Books, 1990).

33. See chapters 1 and 2.

34. I am very grateful to Professor Nikos Salingaros for discussion which helped me to get this point clear.

35. This topic is discussed extensively in Book 2, where the dynamical origins of the distinction between the action of nature and the action of human designers is made clear. That explains how it is that the fifteen properties occur so often in all naturally occurring systems; while, in human artifacts — buildings, and works of art, and our environment — they occur infrequently. They occur in buildings only when human beings are able to act as nature does. See Book 2, THE PROCESS OF CREATING LIFE, chapters 1 to 4.

36. In Book 2, chapter 2, I shall show why the unfolding of wholeness by structure-preserving transformations must inevitably create these fifteen properties, when wholeness is allowed to unfold naturally.

In chapters 1 to 6, I have laid a foundation for order to be understood as some degree of living structure, a well-defined structure that occurs in varying degrees in buildings and in every part of space.

Now, in Part 2, I come to a second view of the same subject matter. In the next five chapters, it will turn out that order—and living structure—cannot be fully understood if we regard them merely as something in Cartesian space, a mechanism separate from ourselves. Rather it turns out that living structure is at once both structural and personal. It is related to the geometry of space and to how things work. And it is related to the human person, deeply attached to something in ourselves, even emanating perhaps from ourselves, in any case inextricably connected with what we are, who we are, how we feel ourselves to be as individuals and persons, beings whose lives are ultimately based on feeling.

This revelation—and after seeing what I have to say about it you may agree, I hope, that it is a revelation—means that the nature of order as I have defined it, in principle at least can finally bridge the gap that Alfred North Whitehead called “the bifurcation of nature.” It unites the objective and subjective, it shows us that order as the foundation of all things (and, not so incidentally, as the foundation of all architecture, too) is both rooted in substance and rooted in feeling, is at once objective in a scientific sense, yet also substantial in the sense of poetry, in the sense of the feelings which make us human, which make us in secret and vulnerable thoughts, just what we are.

This is, scientifically and artistically, a hopeful and amazing resolution. It means that the four-hundred-year-old split created between objective and subjective, and the separation of humanities and arts from science and technology can one day disappear as we learn to see the world in a new fashion which allows us simultaneously to be cold and hard where that is appropriate, and soft and warm where that is appropriate. It can lead to a mental world where art, form, order, and life unite our feeling with our objective sense of reality, in a synthesis which opens the door to a form of living in which we may be truly human.

Above all, this is the threshold of a new kind of objectivity.

CHAPTER SEVEN: THE PERSONAL NATURE OF ORDER

1 / INTRODUCTION: WHAT DOES IT MEAN FOR SOMETHING TO BE PERSONAL?

In our present world-view, the word "personal" is often taken to mean "idiosyncratic." Something is personal if it reflects the peculiarities of a given individual: the fact that you like motor bikes, perhaps; the fact that my favorite color is green, and so on.

To my mind, this is a very shallow interpretation of what "personal" really means. A thing is truly personal when it touches us in our humanity. Thus, for instance, this miniature sketch of a synagogue is personal. It is personal because it raises feelings of a human and personal nature in us when we look at it. It makes us feel vulnerable, slightly weak at the knees. It raises the childish in me. It touches me in some vulnerable part.

None of this has anything to do with the idiosyncrasy of the maker. Nor does it come from my own idiosyncrasy as the recipient. It is a universal childishness which exists in all of us.

Look at the painting of boats by Vincent van Gogh, on the opposite page. Once again, it may seem easy to say that "the painting feels personal." But even if we agree that it is personal, we should again ask just exactly what this means. The trivial meaning of the word "personal," here, might mean that the picture is somehow peculiar to van Gogh, that it stems from his intensity as an individual—his idiosyncracy, perhaps connected to the fact that he lived an unusual life, later became crazy, cut off his ear, and so on. Yet what it really means, and what we feel in these simple-seeming boats is that the painting touches the personal in us. It somehow makes us feel the world more deeply. It is something which comes from, and penetrates to, the most personal feelings we have about the world—the feelings in which we are, like lovers or little children, more absorbed, more happy, more carefree, and more vulnerable.

The trivialization of the word "personal" is part of our present popular culture, immersed in mechanistic cosmology. But from the point of view of the world-picture in this book, "personal" is a profound objective quality which inheres in something. It is not idiosyncratic but universal. It refers to something true and fundamental in a thing itself.

I believe all works which have deep life and wholeness in them are "personal" in this sense. Indeed, this quality is an essential and necessary part of what I have identified as life in things. When we deal with the field of centers, we are dealing with a realm of personal feeling in which feeling is a fact—as much a fact as the radiation from the sun, or the swinging of a pendulum.

When the field of centers is authentic, it is always personal. If it appears to have the right structure but is not personal, it is empty

structure, only masquerading as life—and, in every case like this, it will turn out that we have misjudged it structurally. The existence of a personal feeling in a thing or system is not

a subjective quality of limited validity, but an objective quality whose existence is as fundamental to any given situation as the more mechanical facts to which we are accustomed.

2 / OUR EVERYDAY PERSONAL FEELING AND THE FIELD OF CENTERS

To make it more clear how the field of centers and our deep personal feeling are connected, it is useful to consider some everyday examples.

For instance, almost everyone loves flowers. Few things in the world are quite as moving as a meadow full of wildflowers in early spring: buttercups, daisies, tiny orchids, forget-me-nots, wild roses, cowslips, primroses, wild hyacinths, and dozens of tiny flowers so common that we

hardly know their names—white lilies of the valley, yellow ragwort, sky-blue bluebells, scarlet pimpernels. I don't know if anyone has ever asked just why flowers, of all things, should seem so especially lovely, so beautiful to us. But the idea of wholeness explains it very well indeed. A flower is one of the most perfect fields of centers that occur in nature. And flowers in groups, on bushes, clumped, strewn in a meadow together

create highly complex living fields of centers, perhaps among the most beautiful in nature. If it is true that the field of centers, by itself, is so deeply connected to us, and stirs our feelings, our passion, then of course a meadow full of flowers — one of the most elaborate and simple fields of centers — will have those touching quality we know: depth, tenderness, and longing.

The same phenomenon, the same emotional power, exists in other ordinary things. Consider, for example, a child's birthday party and the high point of the party, the moment when the cake is brought in with the candles lit, and placed in the middle of the table. The table itself is LOCALLY SYMMETRICAL with a BOUNDARY and a STRONG CENTER. To make the boundary more solid, we put the place settings around the edge, each one itself destined to be a center. And to mark the main center, we place there a great jug

of flowers, or the cake itself, making a GRADIENT toward the middle. And then, at each place setting, we put a small place mat, with the knives and forks arranged around it in symmetries to create the center more firmly, and to create detail at the boundary of this smaller center. To make the place even nicer, we will perhaps use a lace table mat, which itself has a major center and a lacy, imbricated edge, again making still smaller centers around the center.

The big jug of flowers that fills the center of the table might perhaps have two candles, one on either side, to mark it and to form its edges. The minor center, the birthday cake itself, is also decorated with a ring of small birthday candles in ALTERNATING REPETITION, marking its boundary, forming a chain of centers, leaving the central space in the middle of the cake empty (THE VOID) for the name of the person, or an ornament.

Each individual candle itself even has the same structure: a body marked at the top end by a boundary—the flame—which is itself a strong center, dark in the middle where the wick is, and bright around the edge, where the flame is burning. CONTRAST exists in the color of the inner flame and outer, and GOOD SHAPE is found in the licking of the outer flame.

We might say that the presence of this structure is incidental to the birthday, that what moves us, what touches us, is the importance of

the occasion, the friends gathered, the presents, the excitement. But the point is that it is this structure precisely—the field of centers in a simple and pure form—which we use, at just this kind of moment, to cement the occasion, to celebrate it. It is this structure which has the power to give the occasion meaning, and which leaves such touching feelings in us, such poignant memories, and so increases our power to feel.

The same occurs in other everyday structures connected with deep feeling. Consider, for example, a woman's wedding ring. The ring itself is a center, the jewel set about with smaller jewels. Or, more strikingly, traditional costumes. Look, for example, at this African woman, and the way her dress, over and over, contains the field of centers to a high degree. One might say this is accidental. But can it be accidental that the other dresses and costumes which people wear for more ordinary occasions so conspicuously have less of this structure in them?

Or consider a simple jar of flowers. This has the structure of centers in it to a great extent. It is so ordinary, so humble, but it has this power in it. And if you doubt that, ask yourself why all the possible related things which have less of this structure in them are so much less touching, so much less deep. A vase with beautifully chosen

branches in it, for instance, may be pleasant, a tribute to nature, even highly aesthetic in a sophisticated sense, but it is not likely to have the same power to touch us unless we choose branches which have leaf buds on them in spring—when once more it begins to have more of the fundamental structure in it. Or consider a flat plate with flowers strewn on it—also very nice, but again with much less of this structure and much less power to touch us unless it is, perhaps, a single deep plate with a single blossom floating in the middle, as we might find in Tahiti or Japan.

Even a simple act like shaking hands, as a structure, has these properties in it. There is the LOCAL SYMMETRY of the two arms, the knot, the DEEP INTERLOCK when the hands clasp, the creation of a BOUNDARY and of a center in the same moment, the ALTERNATING REPETITION formed by the actual motion, by the shaking itself, the NOT-SEPARATENESS formed between the people. It may seem absurd to insist on these details in something so commonplace as shaking hands. Yet we all feel the power of the gesture, and we shall make no progress in our efforts to shape the physical world until we fully understand the presence of this structure in nearly everything that takes on meaning.

The same is true with the Indian namaste, the greeting in which palms are placed together, as in the western mode of prayer. Once again, the hands form a LOCAL SYMMETRY, with a profound STRONG CENTER being formed by the hands, the body, the face, and the body of the other person — the field of this center magnified by the GRADIENT of the fingertips stretching upward, forming a VOID above.

The process of producing and responding to centers is one of the most fundamental of all human processes. It is completely natural in the most ordinary way. A daisy chain, a birthday cake, a wedding ring, a bunch of flowers, the setting of a table — each of these widespread and common things is an example of the field of centers in everyday life. Each brings with it connections to an ocean of personal feeling.

Much of the concentration of feeling in a culture is placed into these vessels and others like them. It is the field of centers which reinforces the feeling in these things. It is the field of centers which thus helps give the most ordinary events their meaning.

---

3 / WHOLENESS AND FEELING

Living structure is, by its very nature, personal and feeling-endowed. The field of centers exists in a thing to that degree to which the thing has personal feeling. To show that it is indeed a matter of degree, visible in shadings, I start with a simple comparison. I take two blank sheets of paper, and put them a few inches apart, side by side. I leave the left one blank. On the right one, I draw a small diamond-shaped dot in the middle of the page.

Most people will agree that there is more feeling in the right-hand paper. It is more personal. It is also true that the field of centers is more strongly present on the second sheet than on the first.

You may say, “Why did you choose to put a diamond in the middle of the paper?” Suppose I had put a little irregular curved line somewhere on the page. Would this still do it? Wouldn’t almost anything put on the piece of paper have more feeling than a blank sheet? After all, a blank sheet of paper is so impersonal that the comparison doesn’t prove much.

So let us also take a third piece of paper, and draw an irregular squiggle on it, and let us now put this piece of paper to the left of the blank one, thus, as in the second row of drawings (next page). In this case, the paper on the left, with the squiggle, has less feeling and is less personal than the one with the diamond. It has even less feeling than the sheet which is blank.

Let me explain this in terms of the field of centers. If I look at the right-hand sheet of the three, the world seems to tie itself together, it cen-

ters in on the diamond, I feel a focus or a concentrated knot in the fabric of things. This simple field of centers is coherent. In the middle sheet, I do not feel this so intensely, but still the page fits, in a reasonably calm way, into the world: there is still a coherent field of centers, so that there is still connectedness, though not as much as in the right-hand sheet. In the one on the left, there is a sense of disturbance: the squiggle interacts with the page in such a way that even the page itself no longer fits nicely into the world around it. The field of centers is incoherent, and the overall connectedness has been disturbed.

In the sense I am describing, the sheet with the diamond-shaped dot in the middle creates the most wholeness in the world. The one with the squiggle creates the least. In addition, the one with the diamond has the most personal feeling, and the one with the squiggle has the least.

Why do I say that the one with the diamond has the most personal feeling in it? I can explain that by using the following experiment: suppose, as in chapter 9, I ask you to tell me which of the three you would pick as a picture of your wholesome self, or your own soul. I think you will pick the right-hand one first, the middle one second, and the left-hand one third. You may agree with this, but still wonder why I call the diamond personal. It perhaps does not seem personal in the ordinary sense.

To convince you that it is indeed more personal than the others, let me propose another thought experiment. Suppose you are with a person you love very much. Imagine you are comfortable, happy, loving, and childish with this person — also vulnerable, and not afraid of being vulnerable. Perhaps you may even feel like a little five-year-old in the degree of your trust and vulnerability. And suppose you have just made the three pieces of paper we have been looking at.

Imagine now that you want simply to give one of these pieces of paper to this person as a funny, special present, as an expression of your feeling — a tiny gift, which will flutter away in the wind five minutes later, but which you want to give in such a way as to share your inner secret with this person. Which of the three will you give? Most likely, you will give the one on the right. The one with the diamond feels valuable, feels worth giving, feels the most intimate of the three.

I do not insist that this is true. But I ask you to make a note of the fact that it might be true that what is personal can be directly and clearly identified in the realm of feeling—and that it happens to correspond to the presence of the field of centers.

Let us go on to a more complicated case. Here are three drawings of women by famous zoth-century artists: Pablo Picasso, Henry Moore, and Henri Matisse. The same distinctions of degree in the "personal" that are illustrated in the three tiny sheets of paper also occur in these more complex drawings. After careful examination, comparison with the fifteen properties, and so on, I believe we shall conclude that the Matisse has the strongest field of centers.

It has the most centers, the most powerful centers, and the strongest relationship of support among the centers. It most closely follows the structure described in chapter 4.

The Matisse also has the most subtle feeling, and the most personal feeling. This is true, I believe, regardless of how you evaluate the three artists. You may think that it depends on what kind of feeling we are talking about. Are we talking about bold feeling (like the Picasso),

eerie feeling (like the Moore), soft feeling (like the Matisse)?

But I don't mean anything so complicated. I only ask you to say which of the three comes closest to your own most vulnerable and most personal feeling. In that case, I believe that you will choose the Matisse. Once again, the one which has the strongest field of centers and the one which has the deepest personal feeling are the same.

4 / SIMPLE HAPPINESS

Perhaps we are beginning to see that life — because of its structure, the field of centers — is inextricably connected with human feeling. If we look back over the examples of buildings, places, landscapes, paintings, and objects that I have shown as having life, we can see that they also are bound up with, and cause in us, deep personal feeling. They have deep feeling. They awaken feeling in us. They make us feel our own existence. It is this increased feeling of life which we experience in ourselves that lets us know these things are important. We cannot separate them, or our awareness of them, from the fact that they have feeling and induce feeling in us.

This deep feeling is indeed a mark of life in things. It is, from a human point of view, perhaps the most important aspect of life in buildings—because it is the aspect which connects that life, most directly, and most wonderfully, with our own existence, with what it is to be alive. And it shows us that the life in buildings, which makes them work, which makes them alive in themselves, also is connected to us, is personal.

Although within the canon of normal contemporary science we cannot imagine a kind of objective truth which is also personal in nature, this combination is one of the most extraordinary and important aspects of the new structure which I call the wholeness. As the centers deepen, the

personal feeling of the structure increases. If its personal feeling does not increase, its structure is not really getting deeper. Precisely this feeling component is its extraordinary property.

Further, and very fundamentally stated, we become happy in the presence of deep wholeness. When I am in a building which has life, I have a happiness in me, a comforting and profound wholesomeness. Unlike those structures pursued by science, which are remote from us and have only mechanical reality, the field of centers is somehow part of us, connected with the very essence of being human.

As a maker of buildings, I simply have the task of making something which creates this happiness in all of us. The nature of the wholeness is such that, when it makes this happiness in me, it also makes it in anyone else who comes in touch with it.

The proper understanding of the connection between objective life in a thing and my own deep-seated happiness is fundamental and goes to the very nature of order itself. Once understood, this connection is capable of healing a rift between us and our understanding of the universe which has existed since the 17th century. In this new understanding, even though we continue to recognize wholeness as a structure which exists "out there," we learn that it is also a real unity which exists "in here," in each person's heart.

In this idea, we shall cross the nearly uncrossable gulf created by the Cartesian view of things and extend our grasp to a new post-Cartesian view. In the Cartesian view, the objective structure of the world is one thing, our own happiness is something entirely different and remote from it. In the post-Cartesian view, the wholeness of the world and our feeling of happiness together are understood to be two complementary things which form a single unity.

5 / FEELING AS THE INWARD ASPECT OF LIFE

Very gradually, as we move through these four books from Book 1 to Book 4, I shall work my way towards the theme that the personal is something inherent in the nature of order and in the universe — not a late comer to blind matter as scientists have thought, but rather, since the origins of time, a vital substrate underlying matter.

This theme — to some ears possibly fantastic — can in no way be regarded as proven. In these four books I merely take a few first steps toward the possibility that it may be so, and that it may one day be recognized — and, further, that architecture, our mother-art, must itself be steered in a direction which allows this to be recognized in our experience. Since I can only walk gradually towards this goal, but since I do also want the reader to see the goal in the distance and be conscious of moving towards it, I shall end this chapter with a few words that perhaps touch too closely on the poetic: but they may help us to steer more successfully when we once more take up sober reason in chapter 8.

I believe the personal feeling I have touched on in this chapter, which is directly connected to order and life, is a mobilization in which my vulnerable inner self becomes connected to the world. It increases my feeling of connection and participation in all things. It is feeling, not emotion. It does not — directly — have to do with happiness, or sadness, or anger.

Rather, it is the feeling of being part of the ocean, part of the sky, part of the asphalt on the road.

Thus the personal nature of order appears in nature as much as in buildings and artifacts. The waves shown on the next page are not just beautiful. The wild rage and beauty which is in them is personal in the same sense, and has feeling. It is personal, even when it occurs in nature, because somehow it awakens "person-stuff"; we may even sense that it is made of person-stuff, and that it connects with the person-stuff in us. To understand order, we must understand that it is profoundly like this. Life is the person-stuff. Recognizing this life in things is equivalent to saying, "The universe is made of person-stuff. I always thought it was made of machine-stuff, but now I see that it is not."

The ocean, with its wild waves, is like this too. It is the personal matter of the universe, reaching its form in us. Even the flock of wild geese in the last photograph in this chapter is ultimately personal — and that is why it is so lovely to us. And when one of us makes a building, we should also be trying to bring this person-stuff to life, to awaken the person-stuff in matter.

Once we recognize that feeling and life are somehow one and the same thing, and that the structure we call wholeness is connected with a ground where matter becomes personal, then we begin to see the depth of the revolution in thought to which the idea of wholeness leads. The external phenomenon we call wholeness or life in the world and the internal experience of personal feeling and wholeness within ourselves are connected. They are, at some level, one and the same thing.

In chapters 3 to 6, I discussed the idea of a center as a focused zone in space where the space begins to come to life. I have wrestled with the

possible meaning of this idea — extraordinary at least to the conceptions of Cartesian mechanics. Now we begin to see that the idea of a center is something which unites objective life — as a quality which exists in space — and the personal feeling that can occur in us. When the center occurs, is intensified, we shall see in the next chapter that the space there begins to resemble the human self, begins to be connected to the personal. A structure which has life becomes more and more personal as it reaches more and

more wholeness, because it becomes more and more deeply imbued with self, with the feeling of which my experience of self is made. Thus the very odd thing which happens is that space itself becomes more deeply functional — more well organized — as it begins to resemble more and more deeply the human person. This is not a comment about psychology, or about the psychological character of art. It is, I suggest, a fact about nature, something which is as much true in untouched nature as it is in buildings.

The ultimate criterion for whether something works in nature, just as in buildings, therefore also depends on the extent to which it resembles the healthy human self. This extraordinary conclusion will give us a clear and succinct summary of the vast gulf between Cartesian mechanics and the view of the universe which I put forward in this book. It also points to the inspiring depths which may exist in the making of a building, and shows us why art is not a trivial, interesting practice—but something utterly fundamental to our human existence, and to the nature of things as they are.

Whenever life exists at all, I believe that it is personal in nature. The waves, the geese flying, the flowers in the meadow are deeply whole and hence alive—and because they are deeply alive, they are deeply personal. Those works of building we aspire to, the greater works, are also those which are most deeply whole, most filled with life. And this life will occur in buildings, as it does in the flowers of a meadow, at that moment when the buildings are most deeply personal.

The connection between order and feeling is fundamental. In some fashion, profound order makes us feel our own existence: it causes deep feeling in us when we come in contact with it. It has deep feeling within itself. Wholeness, even though it is an external phenomenon, is inseparable from our own reality which is presumably internal. Our understanding of building and the

way we make buildings within the understanding of this phenomenon have the capacity to close the gap between objective and subjective, and will allow us to live and work in a world where what is outside ourselves and what is inside ourselves are properly connected.

Wholeness and feeling are two sides of a single reality. Within the modern era, we have become used to the idea that feeling is something we experience subjectively—while life, if it exists, is something that exists objectively out there in the world of mechanics. In such a mental framework, the idea that feeling and wholeness are two sides of a single thing can hardly even be understood.

But as we study the phenomenon of wholeness, as I am trying to do, it teaches us to change our understanding, and to reach a reorganization of our ideas about the world in which this equivalence of living structure and deep personal feeling not only makes sense but is also the most fundamental fact of our existence.

When we experience something which has deep wholeness, it increases our own wholesomeness. The deeper the wholeness or life which we meet in the world, the more deeply it affects our own personal feeling. Centers which have life increase our own life because we ourselves are centers too. We feel more wholesome in the presence of things which have wholesomeness in them, because we, like other centers, are intensified by them.

CHAPTER EIGHT: THE MIRROR OF THE SELF

1 / INTRODUCTION

The existence of the wholeness as an objective, neutrally existing structure, and the possibility of seeing life in buildings as something which emerges naturally from this wholeness as living structure gives us a unifying picture of reality. The concept of living structure holds the promise of understanding architecture clearly and coherently. It gives us a single way of talking about function in buildings, ecology, and the beauty of artifacts in a single language — one which shows us the profound meaning and consequence of all these related facets of the world, and one which, above all, gives us an ethical view of things, because the life (really goodness) of any portion of the world is, in this view, then an objective matter which arises from this structure.

In the next chapters, I shall show that this view has a feature which I have not emphasized so far: it is deeply, and necessarily connected to the human self.

For three hundred years our mechanistic world view has disconnected us from our selves. We have a picture of the universe that is powerful and apparently accurate, but no clear sense how we, our own selves, enter into this picture. This is the famous bifurcation of nature discussed by Whitehead. We have a disconnected vision of reality, which seems secure, which seems strong and objective—but which leaves me out. My experience of self, my own actual person, my existence as I experience it every day is not part of the "objective" world-picture. So, in my daily encounter with the world, I have to make do with a world-picture that fails to connect me to the world. I flail around in it and struggle.

We shall see, in the following chapters, that this situation is changed in the world-picture which I propose. In this new world-picture, based on wholeness and the structure of centers, the connection between the outer or objective world and my experience of the self is profound and immediate. It makes sense. It is pervasive. It is direct.

To approach the new relation between self and world-picture, let us turn again to the question of how we decide which things have more life, which have less. What I have described in chapters 1 to 7 tells us that life can be seen as a phenomenon which depends entirely on the existence of centers in the world. Wholeness is made of centers. Centers appear in space. When the wholeness becomes profound, we experience it as life, in buildings, in other artifacts, in nature, even in actions. The life is able to be more profound, or less profound, because the centers themselves have different degrees of life and the life of any one center depends on the life of other centers. The life of a building thus comes about as a recursive phenomenon in which different centers prop each other up and intensify their life cooperatively. It is responsible for the functional life in a building (the way it works) and for the geometric life (its beauty). They are one and the same thing.

But at the bottom of all this, there is still a puzzling question, the question of the life of the centers themselves. The actual life itself which any given center possesses, its degree of life, is still not entirely clear as a concept. We cannot easily avoid the idea that space itself has the power to come to life—a center is an emerging spot of life in the material substance of space itself. This is disturbing, or at least surprising, because it is inconsistent with most modern interpretations of physics. But even if we want to accept it, we still don't really know what it means. What is it? What is this thing which happens as space comes to life? What is the life of a center, which then multiplies and blossoms to form the life of buildings, ornaments . . . and perhaps even the life of living things?

Everything I have been talking about depends on the operational validity of this idea. It

is this idea of life in space which forms the underpinning for the objectivity of wholeness, and for the basic idea that architecture can be understood in an objective way. All of it depends on the level of belief, understanding, and certainty we have about this life which can occur in things.

We need to know how to measure it, how to estimate the degree of life inherent in a given center, and above all to find out what it is. If the wholeness is as important as it appears to be, it is of course essential—indeed necessary—that we can reach an objective understanding of it, that we learn to recognize it as something which is objectively present in any given part of the

world we pay attention to. Although I have made arguments which depend on the objectivity of its existence, I have not yet presented the empirical methods which are needed to establish it as objective—which tell us how, in disputed cases, we can reach agreement.

As it turns out, the relation of the outer (and objective) wholeness to the inner (and subjective) self, and the empirical methods needed to establish degree of life in different places, are deeply connected. They turn out, indeed, to be two facets of one and the same idea. It hinges on the question: what kind of judgment are we making when we see that one thing has a greater degree of life than another?

2 / LIKING SOMETHING FROM THE HEART

Let us start with the idea of liking. What we do as artists, in the realm of building, really depends on what we like. What society builds depends on ideas that are shared about what people like. But contemporary ideas of what is likable are extremely confused. It is a current dogma that you may like what you wish, and that it is an essential part of democratic freedom to like whatever you decide to like. This occurs at a time when the mass media have taken over our ideas of what is likable to an extent unknown in human history. Thus if one were pessimistic, one might even say that there is very little authentic liking in our time. What people like can often not be trusted, because it does not come from the heart.

On the other hand, real liking, which does come from the heart, is profoundly linked to the idea of life in things. Liking something from the heart means that it makes us more whole in ourselves. It has a healing effect on us. It makes us more human. It even increases the life in us. Further, I believe that this liking from the heart is connected to perception of real structures in the world, that it goes to the very root of the way

things are, and that it is the only way in which we can see structures as they really are.

As we begin to appreciate this liking from the heart, we shall find out a number of important things about it.

1. The things we like (from the heart) make us feel wholesome when we are near them.
2. We also feel wholesome when we are making these things. As we make them, and after making them, we feel whole in ourselves, healed, and right with the world.
3. The more accurate we are about what we really like, in this sense of liking from the heart, the more we find out that we agree with other people about which these things are.
4. What we like from the heart coincides with the objective structure of wholeness or life in a thing. As we get to know the "it" which we like from the heart, we begin to see that this is the deepest thing there is. It applies to all judgments — not just about buildings and works of art, but also about actions, people, everything.
5. There is an empirical way in which we can help ourselves to find out what we really like from

the heart. Nevertheless, it is not easy to find what we really like, and it is by no means automatic to be in touch with it. It takes effort, hard work, and personal enlightenment to understand it and to feel it. It requires liberation from opinions and concepts and ego to experience deep liking.

6. The reasons for the existence of this deep liking are mysterious, not obvious. To plumb them we shall have to examine the nature of things—even, ultimately, the nature of matter itself—very carefully. Nevertheless the reasons are empirical. We may determine, empirically, to what extent a thing has the ability to rouse this deep liking in us. It is not a private matter.²

7. Somehow, the experience of real liking has to do with self. As we find out which things awaken real liking in ourselves, we find ourselves more in touch than before with our own selves.

8. When we find out the things we really like, we are also more in touch with all that is.

The essential thing is that, when we really like something, we generally agree on it. This is so shockingly different from modern ideas that it needs to be discussed very carefully. The main breakthrough in understanding will come when we are able to distinguish the everyday kind of liking (where we obviously do not agree about what we like) from the deeper kind of liking where, as I shall try to show, we do agree. Ultimately it will be this deeper kind of liking, where we agree, that forms the basis for good judgment in the realm of architecture. The crux of my argument will be to show that the deeper kind of liking not only exists but also corresponds exactly to the presence of living structure, and to objective and structural life.

---

3 / AN EMPIRICAL TEST FOR COMPARING THE DEGREE OF LIFE OF DIFFERENT CENTERS

To decide objectively which centers have more life and which ones have less life, we need an experimental method that allows people to escape from the trap of subjective preference, and to concentrate instead on the real liking they feel.

How can this be done? Is there a way of seeing life or wholeness in a building which allows the observer to see life or wholeness clearly as a quality in the object, and to rise above overlays of learned preference, inexperience, opinion, and bias?

I believe there is. The methods I propose make use of the fact that each one of us, as an observer, is directly tuned to the phenomenon of wholeness, and is able to see both wholeness itself and the degree to which it is present in any given situation. It accomplishes this awareness of wholeness, by asking people for a judgment which comes directly from their own feeling. I do not mean by this that we ask someone “Which one do you feel is best?” I mean that we ask, specifically,

which of the two things generates, in the observer, the most wholesome feeling.

In the method of observation which I propose, the observer asks to what degree each of the two things we are trying to judge is, or is not, a picture of the self—and by this I mean your and my wholesome self, perhaps even our eternal self.

Suppose you and I are discussing this matter in a coffee shop. I look around on the table for things to use in an experiment. There is a bottle of ketchup on the table and, perhaps, an old-fashioned salt shaker, both shown on the opposite page. I ask you: “Which one of these is more like your own self?” Of course, the question appears slightly absurd. You might legitimately say, “It has no sensible answer.” But suppose I insist on the question, and you, to humor me, agree to pick one of the two: whichever one seems closer to representing you, your own self, in your totality.

Before you do it, I add a few more words.

I make it clear that I am asking which of the two objects seems like a better picture of all of you, the whole of you: a picture which shows you as you are, with all your hopes, fears, weaknesses, glory and absurdity, and which—as far as possible—includes everything that you could ever hope to be. In other words, which comes closer to being a true picture of you in all your weakness and humanity; of the love in you, and the hate; of your youth and your age; of the good in you, and the bad; of your past, your present, and your future; of your dreams of what you hope to be, as well as what you are?

Now I ask you again to look at the two things, the salt shaker and the ketchup bottle, and decide which of the two is a better picture of all that. In the experiments I have made, more than eighty percent of all the people who ask themselves this question choose the salt shaker. The result is, as far as my experiments can tell, independent of culture or personality. People make the same choice whether they are young or old, man or woman, European or African or American.

But the value of the result and the success of the experiment depends on the question they are answering: and on whether it really is this question they are answering. There are, always, those who choose the ketchup bottle. There are good reasons why they do. Ketchup goes with hamburger. It is an icon, almost, of our modern life; we associate with it because it is ordinary, comfortable, relevant to everyday life, and highly identifiable. Also rather nice. The salt shaker is almost archaic by comparison. Though many people still have this type of salt shaker around, it feels as though it might disappear from our lives, be replaced by another way of dispensing salt. All this is true, and explains why twenty percent of the people who ask themselves this question choose the ketchup bottle. But none of this is relevant to the way I mean the question to be asked. The question I mean to ask is, of the two, which is more deeply connected to your eternal self? Which feels as if it is a better picture of your eternal self, your aspiration, the core of you that exists inside?

The question seems to deal with the deep wholeness of the person—and with the deep wholeness of these two objects. It does not depend on the personality or character of the observer. The question helps people get away from their preference and opinion. Once it is clearly explained and people agree to answer it, the question seems to hold a great deal of promise as a rock-bottom experiment that can reliably distinguish more life from less life.

As far as I have been able to discover, we can apply this question to virtually any two things whose degree of wholeness we are trying to compare. Whenever we compare two objects, we can always ask, "Which of the two is a better picture of my self?" We can do it for pairs of buildings, paintings, parts of a neighborhood, doorknobs, spoons, roads, clothes, tables, chairs, roofs, walls, doors, windows, towers, groups of buildings, parks, gardens. We can do it for actions, for pieces of music, for a single musical chord, for choices of an ethical nature, for a complex choice, even for a single stone set in the earth.

Here is another example of this phenomenon at work. In 1985, about a hundred people were at a conference in New York state, where I was talking about these matters. To demonstrate the idea of the mirror of the self, I pulled two objects into the discussion. Both happened to be in the conference room where we were meeting. One was a gray steel working stool with a round top; the other a blue-painted wooden bench.

I pulled these two objects into the middle of the circle where we were talking, and asked people to decide which one of the two was a better picture of their own selves, and explained the question as I have done here. After a few minutes of silence, I asked for a show of hands. All but one of the hundred or so people said that the blue bench was a better picture of their selves. One person said that the gray stool was, for him, a better picture of his self.

The person who chose the gray stool was upset to be in such an isolated position, and became very argumentative. He wanted to insist that he was right, justified, and so on. He

wanted, especially, to argue that there could not be a truth such as this. He said it was obvious that such an issue could be settled only on a person-by-person basis, and that each person would choose something different, according to his or her individual nature. I pointed out to him that, on the basis of this hypothesis, it was very unlikely indeed that ninety-nine people would all choose the blue bench. He became more upset, and more argumentative. I let him talk for as long as he wanted, hoping he would become more comfortable. To the end, he insisted that he was right.

Two weeks later, when I returned home to California, I had a letter from this man: "You'll remember me, I hope, as the fellow at Omega who made an issue of having chosen the stool over the bench. By Wednesday I had let go the issue altogether. It was not worth the degree to which it was distracting me from the material at hand, so I just dropped my attachment to the stool. As a result, by Friday I was seeing both the bench and the stool differently, and had come to discern the qualities in the bench which made it a more whole entity, or capable of representing my most whole self. The question of nourishment was very different for me in that, from the start, I regarded the bench as more nourishing. It was very powerful to witness my perceptions undergoing such a basic alteration. Overall, this is what I took away from the workshop, a fundamental and profound change in the way I perceive things. What surprised me is the potency of emotions that has accompanied this transformation. For days now, as I think back over the workshop, I am acutely moved, as if a very deep part of me is recognizing some long lost elemental truths."

My experiments show that, in general, people agree to a remarkable extent about which objects are more, or less, like their best, or better, or most whole selves. Very surprisingly, it appears that this judgment is independent of person-to-person differences, and independent of culture. What is more, this form of the question creates the opportunity for growth. Even if an observer

is at first confused by the question (and perhaps also by the question, "Which of the two is more alive?"), it allows him to teach himself and to grow in his ability to judge the matter.

As we shall see, the question forces a kind of internal development and growth in the observer, so that he or she gradually comes face to face with what wholeness really is, and is able, step by step, slowly to give up his or her own idiosyncratic ideas about what is beautiful, and replace them with a lasting accuracy of judgment.

In order to understand the objectivity of life or wholeness as determined by the mirror-of-the-self test, it is essential to make sure that the question itself is correctly asked and understood. Thus, for example, the question does not mean "Please tell me which of these two things is more like you, in an autobiographical sense." Nor does it mean "Which of these two things reminds me more of my idiosyncrasies?"

Neither of these questions would accurately include the idea that the thing is a mirror of

yourself, as you are and as you hope to be. There is an awareness of the beauty of potential that lies in each one of us which is crucial to the question. If we seek a thing which reflects this potential as well as what we have achieved, it is entirely different from choosing a thing which merely reflects the one-sided imperfection of the present idea we have of ourselves.

Again, neither of these questions would accurately include the idea that the thing must reflect us truly as we are: that is, with our loving and our hating, our triumph and our lament, our hilarity and our abyss of fear. A thing about which we choose to say, "That looks like me" or "That looks just the way I feel," is always one-sided, has our peculiarity in it. It will be in no sense universal and this is because, in our immaturity, we try to forget the so-called bad things about our selves, our incapacities, our weakness. But when we look for a thing which reflects everything, both our weakness and our happiness, our vulnerability and our strength, then we enter an entirely different domain. The question takes on a different meaning, and we find that different people do usually choose the same things.

We can put the question in a more primitive sense, perhaps, by asking: which one of these two things would I prefer to become by the day of my death? That tends to remove the idiosyncratic and autobiographical cases very clearly. A student of mine formulated the question in another useful operational way. He said, "Assuming for a moment, that you believed in reincarnation, and that you were going to be reborn as one of these two things, then which one would you rather be in your next life?"

On these pages, there are examples of the kind of distinctions we get from these experiments. In each pair, it is the upper one, or the left-hand one, which is a better picture of the self. We may also ask: which one has more life? It is almost the same question.

Here are two cups: a small mocha cup and a larger coffee mug. Which of the two is a better

picture of my self? Eighty-five percent of the people asked say that the smaller one is better. A caution here, as in the case of the ketchup bottles: the larger coffee mug is more convenient and, many of us, if we are coffee drinkers, might well prefer it, even demand it, as the one to drink our morning coffee from. That, of course, is not the question being asked. The question being asked is really quite rarefied: which one is a better picture of our own true self? This almost esoteric question gets the other answer. Most people choose the small, delicately shaped and flowered, tiny cup.

Or take the case of two tools: an ax and a Phillips screwdriver. Which of the two has more life? Eighty-eight percent of people say that the ax has more life.

Or consider coins. My photograph shows an American nickel and a dime. Most people say that the dime has more life than the nickel. In case you think their choice has to do with monetary value, you should know that sixty-five percent also say that the dime (10 cents) has more life than a quarter (25 cents): the effect has to do

IN EACH CASE, THE LEFT-HAND ONE IS MORE LIKE A PICTURE OF THE SELF

IN THIS CASE, THE UPPER ONE IS MORE LIKE A PICTURE OF THE SELF

THE LEFT-HAND ONE IS MORE LIKE A PICTURE OF A SELF

The Japanese jar is quite beautiful; I do not place it on the right hand side here, to imply that there is something wrong with it. I merely wish to say that, relatively, the Turkish jar on the left has more of the self quality than this jar has.

with the concentrated small brightness of the smaller coin.

Here are two items of office equipment: a bottle of rubber cement, and a pair of scissors. Which one seems more alive? Ninety percent of people say that the scissors have more life.

It is very important to emphasize that, like the earlier judgment of life or the judgment of deep liking, this judgment—"Which one is a better picture of my self?"—has nothing to do with preference. When I say that one spoon is a better picture of the self than another, I do not say that you, the reader, do, or should, prefer it. I merely state, as a fact, that it is a better picture of the self, and that this fact will be visible to most people who take the trouble to examine it.

A few years ago I was with a friend, Bill Huggins, in London, describing these facts to him. He became intrigued and asked me to show him some examples. I happened to have with me a catalogue of an auction, at which some carpets were to be sold. On one page, two carpets were illustrated in color.

I asked Bill to compare the two, and to tell me which one he felt better described his whole self, all of him, good, bad, past, present, and what he could be—in short, the same question which I have been writing about.

He sat and looked at the pictures for a long time. Finally, he said, "This is extremely difficult. The first of these is beautiful. I like it, it has bold colors, beautiful graphic quality; it is

well designed, forceful . . . and so on. The other one is much softer, quieter. I don't even like it, and yet, in some strange way, when you ask me this question, it seems that the second one, not the first, is a better picture of my self."

I said, "Well, please forget what you like or don't like. I don't care whether you like one better than the other, nor if you think one is better designed than the other, nor which one you consider more beautiful. All I want is that you should look and look and look, until it is clear to you which one comes closer to being a picture of your self as you are and as you want to be."

"In that case," he said, "I have no alternative. I must choose the one which I don't like." And he pointed to the second one.

The carpet which Bill didn't like, but which he found to be a truer picture of himself, is a rare Ersari prayer rug. The other carpet, which my friend liked better but did not choose as a picture of himself, is a Daghestan prayer rug, brightly colored, pretty, but less important. Novices in the field of carpets would often choose the Daghestan because they are attracted by its colorful prettiness. Carpet experts would all recognize the Ersari as a more serious carpet because it is "better." It is also worth a lot more money.

By using the picture-of-the-self criterion, Bill transformed his level of seeing from that of a novice to that of a beginning expert in a matter of a few minutes.

4 / THE MIRROR OF THE SELF

Let us now look at a few buildings and artifacts which are very good pictures of the self. We might start with the yellow tower from the preface (in color on page 11). Some of the buildings and objects and situations shown in chapter 1 are very good also (pages 31 - 57). And on the next five pages, starting with the barn below, there are still others which are very, very good.

If I ask you what you think, you may agree that these things are full of life. You can see the field of centers the yellow tower creates: the graded sequence of smaller centers formed by the roofs, the perfect placing of the windows, their perfect shape within the wall. But I can also ask you a different question — whether this yellow tower or the barn below in any way reminds you of yourself. The remarkable thing about the tower, and the same goes for the barn, is that, to

a deep degree, for me, for you, it is a picture of our own selves. I believe you may agree that it is also a picture of your self. It is a picture of the self or soul of each one of us. It is not hard to observe this, but it is very hard to understand it. The tower was made around A.D. 600, fourteen hundred years ago, by people who were utterly different in their habits and thoughts from us. It was made at a time which was, culturally speaking, alien to nearly everyone alive today. Similar things may be said of the barn: and of the buildings and artifacts shown on the next four pages. And yet these buildings form a picture of something which is in you and in me as we are today. Somehow, that "something" exists at a deep enough level to transcend time and culture. It reflects, to an astonishing degree, the self which is in every person, regardless of history,

culture, and personal idiosyncrasy. I maintain that in every case the buildings which do well as pictures of the self are those which have living structure—hence the field of centers—most profoundly.

In chapter 4 I defined living structure, and showed how it allows us to distinguish buildings which are alive from those which are less so. We

looked at the centers they contain, and the ways these centers form a field; in those which have most life, the field is most intense. Even when we looked at a pairs of examples which are superficially similar, we saw how in each case the one with more living structure, where the centers are stronger and the field is more intense, are also likely to be judged as having more life.

We may now see that the mirror-of-the-self criterion, applied to various similar building pairs, gives the same judgments. Compare, for instance, this pair of high buildings, one the monastery apartments on the Greek island of Mount Athos, one the Detroit, Michigan apartments designed by Ludwig Mies van der Rohe. In terms of the field of centers, it is clear that the monastery has a more powerful field of centers and more living structure; the centers are individually more powerful; and they are more subtly unified. That translates, too, into the fact that the monastery has more life than the Detroit apartments, if we make the judgment of degree of life, in the manner suggested by chapter 2. If we use the picture-of-the-self test, we get the same result. The Mount Athos monastery is a better picture of your eternal self than the Detroit apartments.

On the following pages, I have presented a number of other pairs of examples. In each case, we may see which of the two is more like a picture of the self, and, again, which of the two has more life. In every case, the one which is the better picture of the self also turns out to be the one which has more life, as well as a stronger field of centers.

IN EACH PAIR OF EXAMPLES, THE ONE ON THE LEFT IS A BETTER PICTURE OF SELF

IN EACH PAIR OF EXAMPLES, THE ONE ON THE LEFT IS A BETTER PICTURE OF SELF

IN EACH PAIR OF EXAMPLES, THE ONE ON THE LEFT IS A BETTER PICTURE OF SELF

IN EACH PAIR OF EXAMPLES, THE ONE ON THE LEFT IS A BETTER PICTURE OF SELF

The mirror-of-the-self test and degree of living structure both give us a handle on life. When living structure occurs in space, it produces a configuration which we recognize as if it were our own self. The more intense the field, the stronger the centers, the more intense the feeling that it is a picture of our own self.

It is very important to recognize that (like the criterion of "life") the quality of being a good picture of the self is always a matter of degree. Some of the examples I have given compare items which are extremely different in the degree to which they reflect the self. I do this for clarity. But it may give the false impression that some things have the picture of the self and others do not have it. This would be wrong. Everything has life in greater or lesser degree.

When we measure degree of life in things by means of mirror of the self experiments, we get the same kinds of results about relative life in things as we get when we calculate density of living structure, or use the presence of the fifteen properties within a thing. In many of these examples, neither has the mirror property to a strong degree. But in each case, you can see that one has it more than the other. As you see, for almost any pair of things (provided they are roughly similar in scope), we can choose the one which has it more and the one which has it less. Consider, for instance, the two examples of corner buildings. The first has more self, probably because it is not trying to communicate an artificial image. I must emphasize that I do not especially like this left hand one; nor do I recommend it as a beautiful building. In fact I think it is not. I merely say that, if you perform this experiment, you will find that the left, not the right, relatively of the two, is more of a picture of your self.

Other pairs are subtle, the two examples of Romanesque doors for instance. Both are arched. Both are beautiful. But if you stay with the example, keep looking first at one, then the other, each time asking yourself the question, Which is more like your own true self, then gradually it becomes clear that one is stronger. One is a better picture of my self than the other.

At any level, for any two things, for any two designs, for any two possibilities, we can decide which of two has more of the mirror-of-the-self quality. With this tool, while we are making things, we can accurately gauge which one has more life and more living structure.

Some of the examples I have given are a bit obvious. One wonders, Is it worth going to such lengths when this merely establishes what we know already? However, the surprising, and the important, thing is that the mirror-of-the-self test does not correspond to our everyday sense of what we like. When we really concentrate on the life in things by checking how much self they have, we find that sometimes, yes, the test does confirm our liking, or our preference. But at other times, it gives us quite different results, which are not stereotypes of good design but which surprise us, shock us out of our complacency, and make us recognize that we are confronted here with an autonomous phenomenon, that has a great deal to teach us.

5 / THE SURPRISING QUALITY OF SELF

It is very important to recognize that asking what has most life is not the same as asking what people "like." For example, among architecture students in the 1980s, at a time when post-modernist images were very popular, many students liked the lower building of the pair on page 336 (Mario Botta's cylindrical house and a traditional Swedish cottage). The lower house con

formed to their idea of what their teachers had told them, and what a good postmodernist building ought to be, because it has certain funky, crazy images in it. Seventy percent of the students (in 1988) said that they liked the Botta house more than the other. But when we asked the same students which of the two buildings had most life, sixty-five percent identified the upper one.

Notice that the number of people who said this was not as big a majority as in our other experiments. This happened because the question introduces a certain discomfort. For 20th-century architecture students, the question probed to the core of their assumptions and raised questions about their liking for the Botta house. Some of them still clung to the Botta house and were not willing to be upset by the question — hence the smaller majority.

But in spite of its discomfort, the question has its own truth. Many of the students could not escape from this truth, even though it made them squirm because it challenged their values. This life or self in things is surprising, and it takes an enormous amount of attentiveness to be constantly awake to it and to keep it clear and distinct as something different from stereotyped liking or preference.

Equally, what has more life is not the saccharine quality of "traditional architecture." On page 337 there is an example which goes the other way: a rugged car repair shop versus a plastic, "nice" restaurant. In this pair of examples, we see that what has more life is not necessarily sweet or delightful. In the comparison of these two examples, the car repair shop has more life. Yet it is industrial, mechanical, and dirty. The restaurant, which is nice and too sweet, has less life.

One might argue that this is because the machine shop is more complex. Is this true? No, it is not. What has life is not always complex in appearance. In the pair of examples on page 339, the Danish cottage is simple and informal. The

baroque example of the dome of Les Invalides is highly complex, ornamented, and formal. It has less life, less self.

Is it then a question of what is informal compared to what is formal? No, it is not. The example on page 338 shows a case where the formal has more life, and the informal has less. Hardwicke Hall, built in England about 1600, is highly formal. The hippie, shingled, rustic house, built in California about 1960, is highly informal. Yet it has far less life and less self.

Is it then a question of what is ornamented or unornamented? On page 340, I show the Eames house, built about 1960. It is spare and mechanical. But it has more life than Mrs. Hooper's chocolate shop in Oakland, California, a fake traditional building abundant in ornament.

Yet absence of ornament is no guarantee of self either. The last example, on page 341, shows a Seljuk tomb, massively ornamented in black and dark blue tile. It possesses an immense amount of self. The stark, unornamented tombstone shown below it is lacking in life almost altogether.

Here it may be hard to make the determination clearly. If you ask yourself which of the two tombs is more appropriate as a tombstone, it is possible you may find the stark one more appropriate, more "death-like." Certainly it is more conventional. And for some tastes, the highly ornamented, even colored, Seljuk tomb may seem a bit extreme as a tombstone. But I am not asking which is a better tombstone. I am asking only: which one is a better picture of your whole self? And to that question, whether reluctantly or not, I think one cannot help answering "the Seljuk one."

What has self and what doesn't cannot be captured by any simple formula. Though I believe it is captured accurately by the field of centers and its degree of centeredness, empirically that too is not so easy to judge. The concept of the mirror of the self is an undefined primitive, which has to be attended to. It is fundamental.

IN THIS FIRST PAIR OF EXAMPLES, THE SOFT TRADITIONAL BUILDING HAS MORE SELF THAN THE HARD, MECHANICAL ONE

Partial explanation: Why does the less formal have more self here, while the more formal has more self on page 338? In and of itself, more formality or symmetry and preconceived schemes by themselves are not a strong basis for being like self. What touches the self is the question of the force that generates them, and the place in the world that is finally created. The symmetry and the formality of the Botta house is an intellectual construct, removed from personal feeling or from any real functional need. Here the cottage goes much deeper, to a result of real life and real need. Yet in another case (the third pair of examples), the formal and symmetrical structure is the deeper of the two, and resembles self more deeply than a rambling, homely structure.

IS SOFT AND TRADITIONAL THE CLUE TO "SELF"? NO IT IS NOT. IN THIS PAIR OF EXAMPLES, THE MECHANICAL AND HARD WORKSHOP IS MORE SELF-LIKE THAN A "NICE" RESTAURANT.

Partial explanation: Our intuitive preference toward the workshop comes from the fact that in the workshop there reigns a kind of "messy" order that has been created by the real everyday needs of the people who work there. This order, where every tool finds its own place, comes from functional requirements: keep the shop floor clean, every tool easy to reach, enough space for the car to move in and out, for repair. In the case of the restaurant we can recognize, also, an order. But the order is not as genuine, not as real. It is more arranged, a kind of artificial order all planned to draw people in, to sell more.

IN THIS THIRD PAIR OF EXAMPLES, THE FORMAL AND APPARENTLY IMPERSONAL ELIZABETHAN COUNTRY-HOUSE HAS MORE SELF THAN THE INFORMAL HIPPIE COTTAGE

Partial explanation: The formality and symmetry of the English country house has been generated by a series of real needs — aesthetic, functional, the predominant way of life in that era. So the symmetry is broken to allow for all different kinds of things to take place ... big windows, different shapes of rooms, ornaments, and so on, all have found their place in a relaxed way, a matter-of-fact way, without disturbing the overall geometry of the building. On the other hand, what we see in the hippie house, all kinds of window sizes and shapes, different volumes, roof shapes, create a feeling of arbitrariness, where not enough mass or matter has been felt to glue them together to create a whole. Just as the Botta house is an intellectual construct which does not relate to the inner self, the hippie house is a fashion construct dictated by the rules of an era to express "freedom," to to react against the established order, and therefore, as a construct that expresses only reaction, does not succeed in connecting to deeper feelings.

IN THIS FOURTH PAIR, THE PRETENTIOUS FORMAL DOME OF LES INVALIDES IN PARIS HAS FAR, FAR LESS SELF THAN THE SIMPLE, INFORMAL AND QUIET DANISH COTTAGE.

Partial explanation: Here the extreme stillness of the Danish cottage, the steady rhythm of the wood frame members, the white plaster, all convey an atmosphere of calmness which penetrates our inner life. The massive dome of Les Invalides, encrusted with ornament, and with rigid, formulaic symmetries of the baroque, are only following rules of an aesthetic canon, and have little or no connection to our real inner feeling.

IN THIS PAIR OF EXAMPLES THE PLAIN, LESS ORNAMENTED EAMES HOUSE HAS A GREAT DEAL OF SELF. THE FAKE TRADITIONAL BUILDING IS MORE ORNAMENTED AND MORE SUGARY, BUT HAS LESS SELF, AND FAR LESS LIFE.

Partial explanation: Ornament has to find its own real place, to succeed in bringing forward the beauty and the structure of the bigger things. This is what jewelry does when worn correctly. In the case of the Oakland shop below, the shape and placing of ornaments is arbitrary, quite thoughtless, scattered all over without any relationship to the building itself. Their only purpose is to break the big volume of the roof and the building, and make it "sweet" to sell chocolates to a conventional public. The Eames house, on the other hand, is true to itself, glass and metal, a clear structure with its levels of scale, which does not need further additions in order to exist, except from the trees which surround it. One might argue that the Eames house, like the Botta house, is an intellectual construct, but it is easy to recognize that the intellectual procedure that created the Eames house allowed a series of other factors—a feeling for the surroundings, a playful attitude to glass and steel—to play a major role as well.

IN THE SIXTH PAIR IS A CASE WHERE AN ORNAMENTED THING HAS MORE SELF THAN A PLAIN THING. THE HIGHLY ORNAMENTED SELJUK TOMB HAS MORE SELF, WHILE THE COLDER AND MORE CONVENTIONAL GRAVE STONE HAS LESS SELF.

Partial explanation: The Mevlana tomb is full of ornament, even more than the fake Oakland shop. It is all covered with ornament. But here the ornament "springs out" of the matter, is one with the shape of the tomb, it accentuates its length and its roundness, and certainly celebrates life. The scale and the repetitiveness of the ornament, together with the intense contrasting colors, blue and black, find a deeper response in our inner complex self, than the pure, dull, gray, and simple tombstone.

6 / WHOLENESS AND REAL LIKING

So we come back to the question of real liking. As I said at the beginning of this chapter, we live in an era when people's likes and dislikes are controlled by dubious intellectual fashions — often supported by the media. This is only a more extreme form of the way that in all human societies people's likes and dislikes have always been controlled by the opinions of their supposed betters. It is only with maturity that we learn to listen to our own heart and recognize what we truly like.

I assert, as a matter of fact, that the things which people truly and deeply like are precisely these things which have the mirror-of-the-self property to a very high degree. This implies further that as we mature, and as we get rid of the idiosyncrasies and fears of youth, we gradually converge in our liking and disliking. We find out that what is truly likable is a deep thing that we share with others.

Let me express this in terms of my friend Bill's experience with the two carpets. According to his own judgment, he liked carpet B more and carpet A less. He then found out that in spite of this A was the carpet which more nearly resembled his own self, even by his judgment. And I now assert that in the end, Bill would have found out that he would have had a more lasting liking for carpet A, even though he himself did not recognize it at the time of the experiment. His guess about what he liked was empirically wrong.

This has a simple empirical meaning. Each thing that we like or do not like may be tested for its staying power. If I look at two drawings for the first time, I may like A more than B. But if I pin the two drawings above my bed and look at them every day, live with them hour after hour, day after day, month after month, gradually I will find out which of the two gives me a more permanent, more lasting satisfaction.

The fifteen properties play an enormous role in helping me to distinguish A and B. If I determine that A has more of these properties, then gradually, over time, I may notice that it has more staying power. As I begin to be aware that the structures have predictive power, then my confidence increases, my ability to judge is refined, and my ability to feel accurately is increased.

This is the remarkable thing. The knowledge of the structure, when used in this way, purifies my ability to feel accurately. It does not supplement my feeling as the basic criterion for life. It helps me overcome the lack of feeling which I have in me as a result of opinion and ideology. I am then in a position to deepen my awareness of life in things and to discriminate or distinguish more finely.

It can often happen that B, which I like most at first, turns out to have a short life in this kind of experiment, and that A, though I did not recognize its value at first, has a more lasting quality which allows me to come back to it again and again and again.

This is what I mean by saying that what is truly liked may be different from what is apparently liked. And this is a matter of judgment and knowledge, not a matter of opinion. It takes a lot of experience to know, in advance, which of the two things will pass the test of staying

power. That is, essentially, what the mirror-of-the-self test makes possible. It establishes which of the two things will be more permanently liked, which has a more permanent and lasting connection with our heart.

This raises a point of great importance about wholeness. The life in things, or the wholeness in things, is not merely an abstract, functional, or holistic life. The things which are alive are the things we truly like. Our apparent liking for fashions, post-modern images, and modernist shapes and fantasies is an aberration, a whimsical and temporary liking at best, which has no permanence and no lasting value. It is wholeness in the structure that we really like in the long run, and that establishes in us a deep sense of calmness and permanent connection.

But the peculiar fact is that it is not so easy to find out what we really like. It is a skill and an art to become sensitive enough to living structure so that we see it accurately and become sufficiently aware of it, so that our liking, as we experience it superficially, is in tune with the real liking that has permanence in us. That is why we need the mirror-of-the-self test. It is an instrument that not only helps us discover living structure and see living structure accurately: it also helps us to discover what we truly like.

7 / LEARNING TO IDENTIFY THE THINGS WE REALLY LIKE

I may have given the impression that the mirror-of-the-self test is a mechanical test which always produces the right answers and which always produces agreement. The real situation is not so neat and tidy. It can take years and years to learn to perform this test correctly. Also, in the process of learning it, one is forced to learn more and more about one's own self. Thus even one's understanding of one's own self is changed by the task of learning to perform this test. Since even the process of applying this test depends on an

evolution of development in the observer, the test is far from mechanical and is not always accurate.

In order to make this clear, I should like to describe in more detail some of the real problems which occur when you do this experiment. First of all, suppose we look at a variety of objects and try to decide which ones are more like the self. In some cases, this is easy, and the experiment gets clear results, as in the salt-shaker and ketchup-bottle experiment. In other cases, it is really hard

to tell. You look at the two objects, and you try to decide which one you want to choose as a picture of your self, and it is very hard; you look and look . . . and finally you pick one. But when you compare notes with other people, you find out that they have chosen differently.

The experiment seems to have failed. But then, after finding out what other people say, or think, or comment on, you look back at the two things, think about them, look some more, and gradually you change your mind. You realize that you chose the one you did because of some extraneous reason — that it seemed slicker; that it had a softness which reminded you of your old family home; that it made you think of X, or Y or Z. But after looking and looking and looking, it gradually becomes clearer that the one you chose is the more trivial of the two, that it is not a very good picture of your self after all, and that the other one which you did not choose at first has more lasting power. So, really, in the long run, it is this other one which is a better picture of your self.

A hardened empiricist who reads this comment may say, "Well, there is nothing here, this is not an experiment at all, just a lot of talk being made to sound like an experiment." But this is precisely the problem. The wholeness is real, and you do gradually approach convergence as you find out whether a particular thing is whole or not, or how much wholeness it has in relation to another thing — but it is very hard to find out. That is the experimental and empirical reality. Sometimes, it can take five or ten years to find out which one really is a better picture of your self.

I myself have experienced this dramatically, many times, in the case of ancient Turkish carpets. I used to collect carpets and did, for years, try to find those in which this quality appears most deeply. I found that sometimes I had to look at a particular carpet for hours, weeks, and even years before I knew how good it really was. But all the time, what I found out was something real. This is not a process in which our subjective preferences are merely shifting (though that can happen too). It is a process in which you gradually find out which one of a group of things is the

most alive. The mirror-of-the-self experiment helps to hasten this process by allowing you to focus, clearly, on the issue at hand — and by helping to drive other irrelevant criteria out of your mind.

Thus the experiment is real and legitimate, but it is taking place within an immensely complex process in which you are both finding out about the relative degree of life in different things in the world and, at the same time, also finding out about your own wholeness and your own self.

As far as I know, this process of finding out about wholeness and living structure cannot be simplified. It is deep and difficult. The confusion, the gradual separation of preferences from living structure, the difficulty of comparing notes and sorting out cultural bias and opinions foisted on us by others—getting through this maze does pay off in the end. There is a real quality which gradually emerges as the true thing which can be identified and relied upon.

What is happening then as we perform this test? Why do I consider this test a reliable way of estimating the relative degree of living structure in a thing? Our own minds are confused by opinions, images, and thoughts. Because of these, we often fail to see accurately the relative life or degree of wholeness in different things. Nevertheless, their degree of life may be gauged by the degree to which the thing resembles our own self. However, even in making this judgment, we can again be confused, because our idea of our own self is also confused by images, thoughts, and opinions. Gradually, as we mature, we learn to recognize our own mind or self as merely a part of some greater thing or self. I can refer to this larger self as the original mind. I am then able to judge the degree of wholeness or the degree of life in a building according to the degree to which it is a picture of this original mind. Since the original mind is part of me (or I am part of it), I have it available to me, in principle, whenever I want to make this test. But I shall succeed in making my judgment only to the degree to which I have gotten rid of mistaken notions of what my own mind is, or my own self.

This is an arduous task.

PERSIAN BOWL AND TILE WITH BLUE CIRCLES

The bowl with the bird looks more friendly. We are attracted more to it at first. The tile with blue circles is more austere, and perhaps more design-like. But in the end, after examining both for a long time, it turns out the blue tile has more staying power ... and that it is, in the end, a better and deeper picture of the self.

KAZAK CARPET AND ANATOLIAN CARPET

At first sight the Kazak is more colorful and more mirror-like. The other is damaged and not obviously appealing. But after long acquaintance, the multiple prayer carpet shown below is profound and lasting in its capacity to be a picture of the self. It may take years to find this out.

TWO PREHISTORIC CHINESE BRONZES

The ram is beautiful and profound. The urn, at first, seems merely weird. But in the long run, the urn has a more definite and pronounced relation to our inner self, and in spite of ourselves, gradually we come to recognize it.

TWO PAINTINGS OF MATISSE

The early Moroccan painting is one of Matisse's great works: it has an immediate feeling and reaches far into the self. As a piece of the self it has power without question. The Sorrows of The King cut paper is at first alarming, disquieting. Slowly its majesty sinks in. After years of looking at it, even if the Moroccan painting is more beautiful, I believe the Sorrows comes much closer to a picture of the eternal self.

Luckily, there is a reverse interaction which helps me get closer to the original mind. As I try to perform this test, as I look at things and ask to what extent they are pictures of my self, as I encounter the contradictions and difficulties which this test exposes in me, gradually I start to get rid of all the things which seem good because of images and opinions—and retain only those which really are full of life. As this process continues, it sandpapers away my opinionated conceptions of my self and replaces them, slowly, with a truer version of what my self really is. In this way, the task of trying to perform this mirror-of-the-self test gradually brings me closer and closer to contact with the original mind. And then, of course, the more I do so, the more useful this original mind is to me as a criterion of wholeness and life in buildings. The purer it becomes, the more accurately I see it, the more accurately I use it to form judgments about buildings.

We see then that life, as it occurs in buildings or in works of art, can be measured. But it can only be measured, or estimated, in a way which relies on the degree of development, or enlightenment, of the observer.

According to the Cartesian canon, this method of observation might not be considered valid. The observational methods of Cartesian science rely on methods which are available to any observer. The idea that a given thing is to be measured, for its life, by the degree to which it is a picture of the self of the observer—or by the degree to which it makes the observer feel wholesome—would appear, at first sight, as the most rank form of subjectivity—just the kind of thing which the Cartesian method was designed to exclude.

But what if, objectively, the phenomenon we call life cannot be measured by any other method? In this situation, the narrow confines of Cartesian method would then be the cause of the problem we face in the construction of an adequate environment, since it would place the idea of life, arbitrarily, beyond the bounds of what can properly be measured or observed. I suggest that the ugly and lifeless environment which we have been building since the 1950s has come about because public bodies and authoritative opinion have been most comfortable with that which can be measured or discussed within the Cartesian framework. This has then made real quality all but impossible.

In order to correct this problem and to bring the life of buildings into the canon of normal scientific discourse, we should adjust our scientific ideas of what can be measured, and how we can measure it.

This is not something new in the history of science, which is a continuous series of adjustments in what we may claim to measure, and how we may claim to measure it. In this history, using the mirror of the self to measure the presence of living structure, though highly unusual, would be merely one more step in the evolution of the observational methods needed to deal truthfully with reality as it is.

I am well aware that the ideas of this chapter may pose tremendous problems for a professional architect, or for a person oriented to the scientific thinking of the past century. The idea that truth is to be found in the self, not in the world beyond ourselves, seems questionable from almost any reasonable empirical point of view. And the idea that, even in the middle of a world where we struggle to understand the "other" through empathy, participation, and anthropological wisdom, we should just now turn to ourselves for ultimate truth, not to that other, seems headed for madness.

But, in all soberness, I believe this is simply true. I have spent my life working with people

8 / MANY CULTURES, ONE MEASURE

from cultures other than my own, in Peru, Mexico, India, Japan, Brazil, Israel, Germany. In many of these cases, I have been successful, I think, because of my desire to be that person, to understand—from the inside, as it were—what it is to be an Indian, a Japanese, a Peruvian; and I have done this by becoming Indian, Japanese, Peruvian—and from the inside, then, knowing what it is to be and feel what people in that culture feel.

I am profoundly aware of the differences which arise from culture to culture, climate to climate, place to place, and have built buildings which reflect these differences hugely. I have no doubt at all that these things must be understood and that the most elementary rules of architecture are (1) ask people what they want and (2) give it to them almost without question, so that the dignity of their inner response is recognized, preserved.

But, when all is said and done, it is my view that this matter of the self, the mirror of the self, lies still deeper. I believe that, in all contemporary cultures, people have been robbed of their heritage, not so much because ancient culture has been destroyed, but more because today's prevailing culture robs people of the feeling that is inherent in them, their true feeling, their true liking.

Although, of course, true liking is different from one culture to another, still, I am more likely to succeed in creating a thing that a Japanese person truly likes by making a thing that I truly like than by following a handbook of modern regulations in Japanese style. The fact is that the worldwide advance of money-based democracy has created a profound sameness which is (so far) based on falsehood, on a denial of what it really means to be human. The proper acceptance of what it means to be human, the work of creating living structure which respects that true inner structure of human beings, is a deeper and more serious matter, by far, than the minor variations which culture creates.

If we get this inner truth right, we can then afford to introduce cultural variation—indeed, it will come naturally, just because when people do what seems like "self" to them, it does come automatically. But following the mechanical objective criteria of modern participatory democracy, or of technical society, or of the money-based economy that has driven out true value from our hearts—that is only cant and hyperbole, something dressed up as good to mask something that is deeply bad.

Since the 1970s I have seen how the truths expressed in this chapter unnerve people. I believe these truths are so deep that they are unnerving, essentially, for all of us who have grown up in the 20th century. Yet although they are troublesome, hard to accept, hard to understand—they go against the modern grain—I do believe that they are true, and must be understood, no matter how unpalatable they seem.

They describe something which, no matter how improbable it seems, is simply there in the world: it is one of the essential descriptions of how things are.

NOTES

1. Many of these points are developed further in chapter 8. They are also developed and extended in the chapters of Book 4, THE LUMINOUS GROUND, especially chapters 2, 3, 5, 9 and 10.
2. Discussion of the aspects of matter which create a connection between matter and self is highly complex, and my attempt to define the connection cover a large part of Book 4. Whatever this self really may be, it is, in any case, personal. It is abstract, universal, underlying all things, yet so intensely personal that throughout Book 4 I refer to it most often as the "I." In Book 4, I suggest that this aspect of matter in which all living structure is rooted may have to be considered material, certainly a part of psychology, possibly a part of physics, and that it is this feature of the world which explains the experimental findings described in the present chapter.

CHAPTER NINE: BEYOND DESCARTES: A NEW FORM OF SCIENTIFIC OBSERVATION

GIVEN TWO VERSIONS OF A BUILDING, A AND B, CAN WE TELL EMPIRICALLY WHICH ONE HAS MORE LIFE? CAN WE DO THIS IN A WAY WHICH ALLOWS PEOPLE TO REACH AGREEMENT ABOUT THE QUESTION—THAT IS TO SAY, OBJECTIVELY?

1 / THE APPEAL TO SHARED EXPERIENCE

The factual character of modern science — what we call its objective nature — arises chiefly from the fact that its results can be shared. The method of Descartes — the observation of limited events that are tied to a limited and machine-like view of some phenomenon — creates a circumstance in which we all reach roughly the same results when we do the same experiments. It is this which allows us to reach a picture which is shared, and this in turn which then leads us to call the picture so created an “objective” picture.

What is vital, then, about any objective phenomenon is that the observation of its essential points lead to shared results. To reach an objective picture of a phenomenon of any kind, we must find a way of observing the phenomenon that gives sharable, and shared, results. Then we may say that the phenomenon is objective. Then we may gradually come to share the same picture.

But the methods described in this book—methods which I believe to be necessary if we are to arrive at an adequate view of life in the world—are not based on the Cartesian way of sharing results. To see the phenomenon of life as it really is, the methods used cannot be tied to the crutch of mechanism as the basis for the sharing of observations and results.

For example, when I was working out, and observing, issues of wholeness and life in a thing, as reported in chapters 1 and 5, I did not try to observe things as if I myself did not exist. Instead, again and again I tried to discern which of two objects was more like a mirror of my own self, which one had more feeling, which one seemed to have more life, which one made me experience greater wholeness in myself, and so on—and then tried to find out what was correlated with the thing that I observed. This kind of observation would have been considered inadmissible in the canon of then-contemporary science. Yet, without it, the very subject matter which I have presented in this book would not even have come into view.

Thus it is not a question of opening the door to subjective fantasy. The matters in this book are as objective—as dependent on experience and as likely to give sharable, repeatable, results—as the experiments and observations that are permitted by Cartesian method. But they extend and supplement the arena of permissible scientific observations in such a way that the self of the observer is allowed to come into the picture in an objective way.

I have expressed the view that space must be considered an almost living entity—a kind of stuff which, depending on the recursive structures that are built up in it, becomes progressively more and more alive. Of course, it is unlikely that this way of understanding space could be undertaken within the confines of a method of observation that insists that everything is a machine. Since the conception of space/matter I describe in this book has precisely the character that it is not machine-like, no method of observation which is obliged to pretend that everything is machine-like can possibly see it as it is, or acknowledge its properties.

Yet the facts of experience that I have shown, and used to build up my new picture of space/matter, are available to anyone. I refer especially

to the fact that different parts of space are seen to have different degrees of life. But precisely because the observational method of Descartes forbids us from seeing these facts—or indeed these kinds of facts—these observations and these observed facts have dropped out of awareness in the modern era. That is essentially how our defective and anti-life view came into being in the modern era.

As I began to write this book, I started with a different kind of observation. I believed, intuitively, that observation of our inner feeling, and the fact that different works of art have greater or lesser impact on our inner well-being, have their origin in real phenomena. I concentrated, always, then, on the depth of feeling which occurs in things—especially buildings. The field of centers—and its profound character of wholeness which makes it the basis of all architecture—were available to my inspection because I used a method of

observation that allowed me to check the relative life of any given work as an objective matter.

I want to emphasize that this method of observation, like the method of Descartes, still refers always to experience. It is empirical in nature. It dismisses fantasy and seeks constantly to avoid speculation. In this sense, it is as empirical as the method of Descartes. But where Descartes only allowed observation to focus on the outer reality of mechanisms in the world, my method requires that we focus on the inner reality of feeling as well.

So, the results I have reported are based on experience, they report experience, and they describe experience. The experience in question is experience of inner feeling. But the amalgamated results of this experience still ultimately refer to facts about the world—the different degrees of life the world has in different places. Because of that, our knowledge of these facts can be shared.

2 / A MORE GENERAL CLASS OF TESTS FOR LIFE

I first discovered the mirror-of-the-self test in the late 1970s. At that time, I was surprised, and delighted, to have found a simple test which allows access to empirical investigation of quality and life in artifacts.

In the years which followed, I discovered that this particular test was only one of a whole family of similar tests, all of which laid emphasis on the wholeness experienced by the observer, as the underpinning of the empirical method.

Nowadays, since use of this empirical method has become the cornerstone of my method of practice, my colleagues and I do not exclusively use the mirror-of-the-self test. It is a little too exotic for daily use, a little too eyebrow-raising for everyday professional work. In recent years, when making comparisons between possible building designs, we are more likely to ask ourselves which fills us with the greatest feel-

ing of our own life, which has the most life, which touches the soul most deeply, which one creates the greatest sensation of wholeness in us. It is this, above all, which is the cornerstone of the test, the observation that the systems with most life have the greatest impact on our own wholeness. It is the observation of this wholeness as we experience it in ourselves, which becomes the cornerstone of the method that allows us to use the distinction between greater and lesser wholeness as we feel it in ourselves to distinguish greater and lesser life in the system being observed.

The reader might wonder why I did not begin right away in chapter 8 describing a more general test based on the observer's feeling of wholeness. However, by the time all this became clear to me in the mid-1980s, I had already written chapter 8; and the cogency of the chapter as

a piece of writing, together with the nearly archetypal aspect of the mirror-of-the-self test itself, made me decide to keep that chapter as it was. The mirror-of-the-self test remains fundamental as a method of observation. It stands as the base on which the other versions rest. But it is not the easiest to use in practice, nor is it the one we most often use as a matter of daily habit.

Other, more general tests are more robust, and easier to use. I find that for daily use, the one that works best is the question: “Comparing A and B, which one makes me feel the most wholeness in myself, which allows me to come closest to my own life, which makes me experience life most deeply?” It is not always easy to answer this question, but it is usually possible.

3 / TECHNIQUES OF MEASUREMENT

The essence of the idea of measurement is the following. The degree of life of any given center, relative to others, is, as I have said, objective. But in order to measure this degree of life, it is difficult to use what, in present-day science, are conventionally regarded as “objective” methods. Instead, to get practical results, we must use ourselves as measuring instruments, in a new form of measuring process which relies (necessarily) on the human observer and that observer’s observation of his or her own inner state. Nevertheless, the measurement that is to be made this way is objective in the normal scientific sense.

The essence of the idea behind this measurement process is that, in comparing two different centers, we ask which one induces, in us, a greater feeling of wholeness. The one which induces a greater feeling of wholeness is the one which has more life. According to conventional wisdom, such a measurement process would appear to be highly subjective, and would therefore appear likely to get different results for different observers. If so, it would be useless, since the whole idea of objective observation would then be vitiated. But the essence of the new method I am putting forward is that, on the contrary, we discover that different human observers report very similar results when they perform this experiment. Their observations converge. And the convergence of observations made by different observers thus gives us the key to the objective nature of the degree of life being observed.

I first began using and testing such a measurement process in about 1978. In the years since 1978, I began to see that the mirror-of-the-self test is only one of a number of possible tests, all related and all similar in essential content. All of them invite the observer to inspect the subjective and interior feeling of wholeness induced in him or her by some system in the objective and exterior world, and to use the results of this inspection as a way of obtaining objective insight about the systems observed.

Versions of the test which I have tried in the years since 1978 include general tests in which I would directly ask a person to report on the relative degree to which he or she felt wholesome in the presence of the two systems being compared, and tests in which I asked a person to report on the relative depth of feeling experienced in the presence of the things being compared. Other tests I have used even include one in which I asked a person to report on the relative closeness to God the person experienced when in the presence of the things being compared. There were many others too. I have since heard of another, comparable test, in which exponents of Akido (one of the Japanese martial arts) are asked to compare the inner state they find themselves when comparing two actions; these Akido-trained individuals are quite used to discerning, and then using, their inner awareness of relative greater harmony in themselves as a measure of the goodness of the action contemplated.¹

In all these tests, the observers use observation of their own inner state, when comparing two systems A and B, to decide which of A or B is the more alive.

Some of the possible questions are:

• Which of the two seems to generate a greater feeling of life in me?

• Which of the two makes me more aware of my own life?

• Which of the two induces (as asked in Akido) a greater harmony in me, in my body and in my mind?

• Which of the two makes me feel a greater wholesomeness in myself?

• Considering my self as a whole that embraces all my dimensions and many internal opposites, I then ask which of the two is more like my best self, or which of the two seems more like a picture of my eternal self?

• Which of the two makes me feel devotion, or inspires devotion in me?

• Which of the two makes me more aware of God, or makes me feel closer to God? 2

• When I try to observe the expanding and contracting of my humanity, which of the two causes a greater expansion of my humanity?

• Which of the two has more feeling in it or, more accurately, which of the two makes me experience a deeper feeling of unity in myself?

All these tests have in common the fact that they ask observers to be very truthful indeed about the extent to which they are experiencing greater or lesser wholeness in themselves, while they are in the presence of the systems being measured or compared.³ The observer is thus asked to report an interior experience while in the presence of the things being compared.

---

4 / THE EXPANDING AND CONTRACTING OF OUR HUMANITY

To illustrate the different possible tests, I describe one more of them in detail: the extent to which the observer experiences his or her own humanity rising or falling, expanding or contracting.⁴ This is yet another particular way of paying attention to the degree of inner wholeness I feel at different moments of the day, in different places, and another way of seeing which thing is most nearly a picture of my self.

If I pay careful attention to my own state, from instant to instant during the day, I can notice that at different times I am more humane, or less: at one instant lethargic, at another filled with loving kindness and appreciation of the world; at another, I am a son-of-a-bitch; at another loving, sometimes perhaps almost angelic; at another caring and concerned about others; at another harmful and hurtful again. In short, if I pay very careful attention to my experience throughout the day, from moment to moment, I can watch, in myself, the continuing expanding and contracting of my own humanity.

For example, some time ago, I was on Telegraph Avenue, in Berkeley, on my way to a record store. I stopped on the street to speak for a few moments with a homeless man who often sits there. I sat down on the sidewalk beside him. He was talking to me about the people he observes, how they are OK and not so OK. Something hard had happened to him just before — I could feel it in him; we sat and talked about it. Then, all of a sudden, he put his hand on mine, pressed three fingers into the back of my hand. He left them there for a few seconds, without speaking. Then, slowly, he took his hand away. During those moments, I felt in me a great expanding of my humanity. My existence as a person, my humanity, was larger at that moment when his

Am I more wholesome—in my soul—when in front of this left hand ornament from a Pennsylvania barn, or when standing in front of this symbolic ornament from Brasilia? Facing the left-hand panel, I feel my humanity expanding; facing the right-hand picture, I feel my humanity diminishing.

three fingers dug into my hand. For a few moments of silent communication, I was more than I usually am: more of a person.

Of course, it didn't last. When I left him, as I walked away, my humanity started dropping down again. I went into the store. A few minutes later, I bought a record and went to the front desk to pay for it. I had a few words with the clerk. He took my credit card. Chit chat. Nice guy. Nothing out of the ordinary. But it was a mechanical transaction. The credit card. It was OK. But, very slightly, my own humanity was diminishing, just a little bit, while I went through the motions of paying with that card.

These things are happening in each of us all the time. At each instant, as I go through the world, because of what happens to me, and because of what I do, my humanity is expanding and diminishing all the time; sometimes for an instant it is a little greater, sometimes for an instant it is a little smaller.

It is not only human situations which cause the expanding and contracting of my humanity. It is everything in my surroundings, my experience, the physical world I pass through, the activities and actions I encounter. Even architectural details are like this. They support me, or they deny me, in varying degrees. An ordinary iron railing may be very positive. It is no big thing, but as I look at it, as I am aware of being with it, very,

very slightly I feel more of a person, a little bit more valuable. Or, on another occasion, I may be looking at a thermostat on the wall, I may feel the opposite. The thermostat itself—the box—is not ugly. It is just ordinary. But when I contemplate it, and contemplate the state I am in as a result of being with that thing in that box, very, very slightly I feel less of a person, and my humanity is falling off again.

Consider the two examples on this page. In the ornament from the surface of a Pennsylvania barn—when I stand in front of it, consider it, and bury myself in it—I feel, to some degree, that my humanity is rising, expanding. But with the ornament from Brazilia, I feel something different. It is true that this ornament is supposed to be symbolic, and is supposed, in some fashion, to represent or suggest a new spirit, an uplifting spirit. But, in fact, when I stand before it, walk into it, consider it, and bury myself in it, what I actually feel is my humanity diminishing.

So, the life in things that I have been writing about has a direct effect on me. A thing with more living structure makes me more of a person, another thing with less living structure makes me less of a person. All the time, as I go through the world, I feel the expanding and diminishing of my humanity. Of course it comes from me and it is caused by me, but it is caused, too, by my interaction with the world; and it is different for the different things which I encounter.

5 / COMPARISONS

This kind of experience happens every day.

When I visited Dallas in 1992, my hosts took me around and showed me various places. We started with the Dallas Art Museum. There is a plaza in front of the museum. It has a huge iron sculpture standing in it. In that place, harsh, austere, hot under the Dallas sun, I feel my humanity less, I am less of a person. My humanity is dropping down. But just outside the museum, to the right, there is a short stretch of sidewalk, perhaps three hundred feet long. Along the sidewalk, there are small light green trees, leafy and breezy; they are small in scale, and the avenue they make along the sidewalk is pleasant, cool, shady, and even intimate. When I stand in there, and walk along the sidewalk, my humanity is lifting again, it is rising. I am, during those moments, more of a person.

Then we went to the Texas Bank of Commerce building. In front of the building, there are seats and bushes. Someone tried to make something pleasant and useful. But there are details which make it funny, not quite right. The seats aren't really seats. They are too narrow, you can't sit on them. They are like images of seats, rather than real seats. But even so, funny as it is, the places on the right and on the left are slightly different. On the right, the seats are interspersed with bushes; this is meaningless. No one sits there. No one likes to be there. There I feel my humanity dropping away again. But on the left, it is slightly different. There are a few bushes which have grown up, creating an intimacy underneath. Even though the seats aren't quite right, this intimacy makes it pleasant to be there; slightly, I feel my humanity rising up again.⁵

One might ask why such an esoteric litmus test as the expanding or diminishing of my humanity is needed, when the examples from Texas (the fountain, the art museum, the little avenue of trees and benches) are so obvious in their quality or lack of it, and all one really needs to

say is that the trees and benches are nice, while the art museum plaza is not very nice.

Indeed, this is true. But it must be remembered that in the late 20th century, judgement of architectural matters had been turned on its head by then-prevailing dogma. Many architects

were intentionally designing things like the art museum plaza, and were intentionally avoiding simple nice places (like the small benches and trees) (for example, by sneering at students in architecture school, especially women students, who did projects of this kind).

The same architects, in order to protect the then-prevailing view of architecture, had gone to a great deal of trouble to erect a false system of values in which living and not-living no longer had any meaning. This had been accomplished by an architectural culture in which some architects openly sneered at the idea of deeper meaning, and did their best to pervert commonsense understanding of these issues in order to shore up the artificial values then current.

The need for a formal way of creating well-defined methods, as I have tried to do here, must

be viewed as an antidote to an extremely difficult (and virulent) situation in which people's common sense had been turned on its head, and many people no longer knew how to respond to life in buildings, in an authentic fashion.

Even to this day it is continuing. The director of the Victoria and Albert Museum has very recently been quoted as giving a glowing justification for his decision to build a monstrosity in London, in contradistinction to the ordinary values and opinions held by people in everyday walks of life. It is shown in the accompanying photograph of a proposed extension for the Victoria and Albert Museum in London.6 In this case the "A" might be the photograph as depicted here, and "B," the photograph with some other (to be imagined) alternative, in the position shown. The building shape of A intentionally

violates most of the characteristics of living structure (I assume it is intentional, in an effort to be artistic, since the diversion from these structural features is too extreme to have happened by accident).

If we ask ourselves whether the addition of this structure to the museum and to the street helps our sense of our own wholeness, I believe the answer is almost obvious, that it does not. Of course, one can apply the other versions of the criterion too. Does the street become a better picture of the deepest self? Does it (in any interpretation) bring a passer-by closer to his own true self? Does it feel alive?

Naturally, there are many significant issues in the construction of such a museum addition. The arrival to the building, the importance of a well marked entrance; the impact of traffic, the

possibility that significant things are visible, or sensed, from the moment of arrival. The connection with the objects to be displayed in the museum. This design might be faulted on any or all of these criteria. But what I want to say is that the criterion of its impact on our own wholeness includes all these. The test concerning the wholeness experienced by an observer is not naive. It goes to the root of the life in that part of the environment.

Thus, with a very simple tool, one is able to determine, with reasonable certainty, and with simplicity of means, the extent to which this building does contribute life to the environment of London.

It is true that sophisticated people might feel almost embarrassed to use such a simple standard, to discuss a topic which, for at least a

hundred years, has been so wrapped in complication (the judgment of a building's quality). But nevertheless that is, in part, the point of what I have to say in this book, and also the point of my post-Cartesian method of observation. It is fairly unambiguous, easy to perform, and gets results very quickly.

Whether we are comfortable politically with the results of this observational method is another matter. The method does not allow foolishness. It is not consistent with foolish star-struck adherence to obscure and impenetrable notions of art. For that reason, some may jokingly dismiss the method, because they see that it cuts to the core of the intellectual game which they are playing. The director of the V&A, perhaps in love with the avant-garde character of his brainchild, might do so. But the test is true, and effective and empirical, nonetheless.[7]

Of course, this method of judging does not only allow us to make global judgments, after the fact, when comparing two designs in their totality. What is even more important is that it provides us with a tool for creating plans and designs. It allows us to examine each step in a design process, making judgments about the life and wholesomeness of different possible next steps, and allows us, at each step, to choose the most wholesome, then to move on to the next decision. It may be helpful, I think, to see this use of an empirical method not merely supporting a judgment but contributing to the evolution of a design, in action.

In the next example I illustrate the entrance to a house in Berkeley, California. The house, which my staff transformed and redesigned, started with the front door and the entrance. The then-existing entrance was gloomy and unfavorable, and the owners wanted to change it. It was not easy to do. So we assembled very rough bits of cardboard, and arranged them, trying to get some kind of glimpse of what would be a good thing to do. As you see in the first picture, we started with a fairly straight approach, indicated here by roughly placed bits of cardboard. This had very little feeling or potential for feel-

ing. Certainly, as something which indicated a sense of life or made one feel one's own soul, it was virtually useless. In trying to see what might do better, at some moment a long sheet of cardboard was bent and placed in the S-curve you see in the second photograph. This was more promising. One felt the beginning of a situation where indeed one's own life, or soul was elevated

by its presence. We then built on, trying to see, again in cardboard, what might be done with such a curve, to make it in actual dimensions of masonry materials. This did become more substantial. Finally, the wall was formed and poured in concrete, more or less in the line shown in the third photograph. The finished entrance is shown on the right.

We see here how a very simple application of the criterion enabled us to make a rather pleasant garden wall and entrance, simply by following the consequences of repeated application of the criterion. This method, used for evolution of all aspects of building design, large and small aspects—plans, conception, structure, volume, layout, details—is the backbone of the living processes described in Book 2.

The example on these two pages, shows some of the deeper and more subtle distinctions which can be made by using the criterion of

the observer's experienced wholesomeness. In the first photograph one sees two mockups, side by side, in adjacent panels. I had these made while building the Julian Street Inn, a shelter for the homeless which I built in San Jose, California. We had four thousand handmade tiles made in our own workshops, to be placed on the second story facade. The rose-orange tiles were going to be laid in a diagonal checkerboard, with gray plaster then filled into the alternating spaces between the tiles. I was now struggling with the way the grid of tiles would meet the window frame. In case A, the tiles would be brought all the way to the frame, and the edge-tiles cut, as necessary, to complete the pattern. In case B, the tiles were held back from the window frame, with the idea that the gray plaster would be made solid in the zone next to the frame.

As the reader can see from the second photograph, I finally decided to use B, rather

than A. This choice was not easy. When one first looks at the two mockups, side by side, one is inclined to choose A. A is more conventional, it seems more tidy; it even seems that somehow may do more justice to "the whole." On the site itself we had the same sensation, at the time we made these mockups. I noticed however, that B, though a little strange, was worth examining closely. I then did the mirror-of-the-self test, in that instance, together with a careful check of my own feeling. I found that when this criterion is used it is B, though unusual, which has a slightly better impact on the increase of my own wholeness. I must

emphasize, here, that this was not easy to see. The judgment was elusive, not obvious at all, and only stood out clearly after my colleagues and I repeatedly asked ourselves this question, comparing A with B, then going back to A, then back to B again. This is an example where simple-minded adherence to "Which one is nice?" or even to "Which one has more life?" might easily push toward A. Only the very subtle and careful examination of one's inner feeling, reveals that B, not A, creates a greater sense of wholesomeness or humanity in the observer, and is therefore more truly alive in the deep sense.

6 / JUDGMENT AND THE PURSUIT OF ARCHITECTURE

The whole problem of architecture, especially the problem in our time, has as its underpinning the fundamental question of architectural judgment. What is good and what is bad? What is better and what is worse?

For us as a society, these question are paramount, since if we can attain a shared basis for deciding these questions, and it is reliable, well-founded, and indeed shared, so that everyone agrees on it, then gradually, our cities and our

environment will get better, simply because the human judgment will gradually push them and nudge them, to get better. But of course, that has not been happening much in recent decades, because there is so much ambiguity about these questions. Anything goes. Everyone has a different opinion. Almost everyone has a different philosophy.

The same is true for every architect, and every builder. If we have a sound, and clear basis for making decisions about what is good and what is bad, what is better and what worse, we can then move through the days of decision making successfully, and we shall have good results. But at present, we have no such tool. We have opinions, certainly. But no reliable source of judgment, that we can truly stand upon. And as a result, each architect, each designer, is a little lost, mentally flailing around trying to do a good job without being sure what that means — all because we have a foundation of quicksand for the judgments he/she/we are called upon to make every moment of the working day.

What is ecologically appropriate, what is socially and psychologically valuable, what is beautiful to the eye, what is comforting to the soul — these are all wrapped up together in the global judgment of wholeness. Using the degree of wholeness the observer experiences in herself or himself as a measure of the wholeness in the system being observed, in similar fashion all of these tests help the observer reach understanding

of the objective degree of life that is present in a system. All of them, used by different observers, will create broad agreement about comparisons.

It is vital to understand that the ultimate goal in these observations is observation of the system in the world, not observation of the observer's reaction. If we compare two mountain streams by checking the degree of wholeness which the observers experience in themselves when in the presence of these streams, it is the degree of life, wholeness, and ecological health of the systems — that is, of the living streams themselves — which is being measured, not the satisfaction of the observers. If we compare several designs for a great bridge, as people were asked to do in the recent debate about designs for the Oakland Bay Bridge in San Francisco, we may see, and feel some to be more alive than others — because they make us feel more whole in ourselves — and those are the ones which have more life.

All these methods are special cases of a very general type of observation that relies on the observer's study of his or her own state of wholeness as it exists in front of different things or systems being observed and that then uses the observer's experience as a measurement on the system being observed to determine that system's objective degree of life.

All this can arise only from our willingness to accept a non Cartesian, or post-Cartesian, form of criterion for objectivity.

8 / EMERGENCE OF THIS NEW FORM OF OBSERVATION FROM PRECEDENTS IN MODERN SCIENCE

Since this form of observation is so new, I believe it may be helpful to show that, even though new, it has continuity with other methods of observation from modern science.

Measuring the life of very simple centers is something which occurs, as a matter of norm, even in contemporary thought. Let us go back to

the original definition of wholeness. The wholeness is a system of centers which, working together, create the gestalt of a given part of space. Now, the task of distinguishing some of the elementary centers which occur, and setting them apart from other fragments of space which are less centered, happens without difficulty in sim

ple cases. In seeing an apple as an entity, or the core of the apple, or the apple pits, something we do every day without thinking, again we calculate and notice that this center is more salient, more coherent, than many other nearby overlapping portions of space. Or, for example, if I look at a black line on a white ground, the black line may be identified as a center. It is distinct, bounded, symmetrical, contrasting in color; its appearance as a center comes about because of these features which cause its differentiation. The objective character of this circle as an entity is well known as a fact of cognitive psychology.

In a similar fashion, I have suggested that the wholeness created by a single dot sitting on a sheet of paper consists of a series of convex segments of space. The wholeness is not defined until we can identify these sets as being more coherent, or more centered, than other possible subsets of space. These judgments, too, are usually not controversial. In fact, the point of the gestalt psychologists' experiments in the 1930s was precisely to show that we all make these judgments in more or less the same way. They identified something they called "praegnanz" as the character which created saliency in figures and made them stand out as wholes — what I call the "strength" of centers. By about 1930, there was already a well-documented literature on the problem of defining greater and lesser strength in centers (then referred to in simple cases as "goodness of figure"). By about 1940, this goodness of figure had been pinned down as being dependent on characteristics like convexity, differentiation, boundaries, and so on, "precursors of the fifteen properties I have identified." This goodness of figure was a weak form of the quality which I call "life."

Let us now consider some more complex and more interesting cases: for example, the way the centers work in the garden of the Hotel Palumbo. If you look at the centers listed on page 111 for the Palumbo terrace, it is unlikely that this list will be strongly questioned by anyone. To that extent, we may say that the relative

strength, or life, of the centers is so straightforward that most people will agree with it. However, in this case, the judgment that certain centers are more salient, and others less, reaches a level of complexity that would challenge a purely mathematical analysis aimed at measuring these centers. It is possible that one day computer programs designed for cognition might be able to pick out these centers and rank order them by their degree of life, but in this case we are moving to a level of complexity where human cognition is a more reliable measuring instrument than any presently available mathematical theory.

Suppose I now consider the Palumbo terrace as a whole and try to measure its degree of life. Here again we have a center—but now a very complex center. Consider the problem of judging its degree of life, compared with the degree of life of some chic restaurant. We now enter the realm of architectural judgment. A person who likes postmodernism may choose the chic restaurant over the Palumbo terrace. The degree of life in the Palumbo terrace is not unequivocally visible. It can be questioned. It is not until I point out how many centers it contains and invite examination of the density of these centers that we begin to see how strong its life is.[11] In a case like this, we do still have the number of centers, or density of centers, as something that can help to settle the argument. But this is an analytical evaluation based on a particular method of counting. It can be used to bolster a doubtful judgment. But the judgment itself as a pure judgment, the measurement itself, needs a direct method.

At the end of chapter 8, I showed examples of comparisons which are still more difficult. In these very difficult cases, like the pair of Chinese bronzes or the pair of Matisse paintings, accurate judgment of which one has more life requires a level of self-knowledge on the part of the observer. This may take a long time to develop, and often does not exist until a person has spent years looking at things, sharpening his or her power of discrimination. In this case, even the rule "Choose the one which generates greater wholesomeness in me"

is hard to follow, because the sensation is so deep, and the self-knowledge required to feel, or know, which one creates greater wholesomeness is not readily accessible.

In recent years, experiments done with such highly complex and controversial cases have begun to show that even they are ultimately objective. Ken Pirsig described similar experiments in his novel ZEN AND THE ART OF MOTORCYCLE MAINTENANCE.[12] One of my students, Cristina Piza de Toledo, established that when we make paired comparisons of things, asking people which has more life, there is a surprising and profound degree of agreement about this quality.[13] The studies of Professor Hajo Neis, in the Department of Architecture of the University of California at Berkeley, have reached similar conclusions.[14]

One might say that these studies are still merely sophisticated judgments of preference. But other experiments have begun to establish that these phenomena, which can be measured by techniques similar to those I mention here, have practical consequences in the world that go far beyond mere pleasure or delight. In 1967, Robert Sommer and Ken Craik made a comparison of rooms with and without windows.[15] This was done at a time when architects were advocating windowless classrooms in schools on the grounds that windows were distracting to children and prevented them from learning. In the study, people were asked to sit in a room and write a story. The stories written by people who had been in rooms without windows, and by those who had been in rooms with windows were mixed up and then scored by an independent person, not part of the experiment, for the quality of being "depressed." A variety of indicators was used. All in all, it was possible to establish, objectively, that people were more depressed, and less creative, while they were in the windowless room than in the room with windows. Of course, this method was still carried out within the Cartesian canon. However, there was a hint here of a method in which the wholeness of the observer's state was the crucial instrument.

Other similar observations, where people are asked to report directly about their surroundings and to judge the condition of their surroundings as nurturing, wholesome, comfortable, and so on, have also been introduced by anthropologists, psychiatrists, and sociologists, including Len Duhl, Randy Hester, and Clare Cooper Marcus.[16] In all these cases, what is presented is the idea that subjective reports of human experience have an important bearing on the evaluation of architecture. However, the jump to the idea that these subjective reports are describing the objective state of an objective system was not made by these authors.

A further step was made by Alice Coleman, in her massive 1985 study of high-rise public housing in England. She used indirect indicators of well-being and wellness to show that many government housing projects were objectively damaging to their inhabitants.[17] However, Coleman's study underlines the difficulty of using the type of observation which I am describing here. The fact that the housing estates she studied are for the large part abysmal as environments for growing families is obvious to most observers. Whether measured by "life," by "wholeness experienced in an observer," or just by plain common sense, it is obvious that they are not nurturing for their inhabitants. In the intellectual climate of 1985, these feelings would not have been considered legitimate or reliable indicators of any objective reality. Indicators such as urine in the passages, on the other hand, were considered reliable, and their measurement consistent with the Cartesian method of observation. Thus, although the observations of Coleman are precursors of the type of observation I am proposing here, her work only illustrates the extent to which, by the 1980s, we had not yet learned to accept such observations as legitimate.

In 1985, reports of people's feeling would not have been accepted as proof of anything except subjective feelings. To make the point that these were objective judgments about something real in the world, the urine in the passages, and other mechanical indicators, were used as a way of

proving that it was hard, legitimate, social science. But this was really a conjuring trick. It was really a roundabout way of addressing the underlying fact that there was something objectively wrong with many housing projects, and a way of trying to get by the fact that the science of that time, had no way of making this a legitimate object of inquiry.

Another similar example is instructive. In Berkeley from 1989 to 1992 there was controversy about an apartment building that was proposed for the intersection at Rose and Shattuck Streets. More than a hundred people came to the hearings when the developer presented his project. They objected, in a variety of ways, and said that the project was unsuitable. However, once again, they felt obliged to express their reasoning in mechanistic terms: "it will create a parking problem," "congestion will increase," "there will be pollution," and so on. What they actually wanted to say, I believe, yet what was only occasionally voiced was that the new proposed building was simply not harmonious with the neighborhood, or fitting for it. It was too big, too high, uncomfortably different in construction character. This observation — clear, legitimate, and shared by a hundred people who turned up (and probably by thousands more who did not) — did not have the scientific or social legitimacy that was required to turn the project down. If they had simply said, "The project feels wrong," this would have appeared to be an inadequate legal reason for stopping the project — because it would have

appeared subjective, not objective. Referring to transportation, parking, and pollution, was intended to give legitimacy to these clear feelings by linking them to mechanistic counterparts. But the essence of the matter rested on the clarity and objectivity of the feeling that the project had to be made smaller in order to be harmonious with the neighborhood.

In all these cases, we see, in one form or another, the raw beginnings of the idea that observation of a person's internal state can give us information which is reliable and objective about the objective living or non-living character of some system in the world outside the person.

So far, the studies I have cited have still been viewed mainly as studies within the realm of social science, showing that psychological considerations should have a bearing on the evaluation of architecture. Their validity has been viewed as a validity within psychology, not within physics. The method which I propose, on the other hand, though continuous with these studies, takes a very important further step. I suggest that these apparently "psychological" methods give objective insight about the objective state of a system in the world and should be considered as measurements of this state — and hence as part of physics.

What I am proposing is that these observations of an observer's inner state are not merely a reflection of a person's attitude or psychology, but can actually can be used to measure something real about the external world itself.

9 / THE CORE OF THE NEW METHOD OF OBSERVATION

The method which I propose is therefore different from currently accepted forms of observation. It goes directly to the intuitions which are widely shared and raises them to a formal level as techniques of observation. You are asked to record your own inner feeling, your own inner wholeness — and this is used then as the measure of the degree of life in some system of the outer world you are observing. Although this technique is new to modern science, it was not unfamiliar to the ancients. Confucius advised that a ruler will only be effective to the degree that he is able to listen to his own heart.[18] It is said that Socrates gave the same advice.

This kind of technique is also the basis of one of the most sophisticated Buddhist canons, the VISUDDHIMAGGA, in which the Buddhist student is taught to recognize, feel, and experience the precise inner state which he or she is in at each instant.¹⁹ The key to this method, as practiced by Buddhists, is to recognize the inner states which are wholesome, and then to move toward those phenomena in the inner and outer world which cause or tend to create this state of wholesomeness in the observer and in which wholesomeness is considered to be the most important and most fundamental internal condition. The VISUDDHIMAGGA teaching recognizes a picture in which our consciousness is made of instants of consciousness, eighty-nine different ones, called "cittas" in Pali. One of the main processes taught by Buddhism is discovering the fact that some of these cittas are wholesome ("kusala" in Pali) and some are unwholesome ("akusala" in Pali). It is interesting that in the VISUDDHIMAGGA there are clear explanations of the enormous difficulty of concentrating accurately on the distinction between wholesome and unwholesome internal states. The task of learning to distinguish these states in oneself is the main method by which a person can make progress.

The idea that a person will, in general, have difficulty reporting his own internal states accurately, and the training techniques which focus on this problem and allow a person to grow more accurate and more familiar with the internal states arising in him, are also the main focus of an entire literature in contemporary psychology, including the gestalt psychology of Frederick Perls and hundreds of others.²⁰

What is new in the method I have advocated is that this time-honored and essential part of human experience, the fact that it is possible to focus accurately on the experience one has internally, is not categorized as a subjective and personal matter. Instead, it is used, and recognized, as a fundamental measuring instrument about the structure of the real world outside the observer.

All this hinges on the fact that, when we pay attention to our own wholeness, we find that the degree to which conditions in the external world do increase our wholeness, is predictable. We find, too, that the effect of these conditions on the human observer is reliable and replicable. The idea is that our feeling is not merely a subjective and changing thing, but that it itself is a reliable instrument — and that the condition, or state of this feeling, is a source of objective truth.

It is, in the end, this measuring technique that provides one mainstay of the claim that degree of life is an empirically observable quality in the world.

---

10 / THE RELATION TO DESCARTES

I revere Descartes. Years ago I remember reading a passage in THE MEDITATIONS, where he said something like this: "If you keep on using this idea of making little thought machines, then observe, do experiments, you will find out if this machine is like the world or not. If thousands of people all over the world start doing these experiments, then after two or three hundred years, we shall know almost everything about the way the world really works."²¹

That is my paraphrase. It is what I remember, and I can no longer find the passage, so I may have embellished it. But when I read this, I was astonished to see that Descartes not only invented the method of observation which in effect we have continued to use unchanged for several hundred years, but that in addition he saw clearly what it would bring. Back in 1641 he effectively foretold the modern history of science.

I should like to call the Cartesian method the first method of observation that allows us to find agreement about the world. Nowadays, this first method of observation — the process of obtaining truthful insights about the world, by

standing outside the world as an observer—dominates modern science. It has become, in effect, the only way in which we obtain objective information about the world.

I believe that what I have described in this chapter may be thought of as a second method of observation. If I am right about its power, it might one day seem comparable in value to the first method—and complementary to it.

The first method has helped us to find out how the world works in the machine-like sense. With it we have accomplished miracles, nearly, in the breadth of our scientific understanding. The second method of observation may bring us further miracles. It may perhaps bring us to the doorstep of another kind of world, in which we see, feel, become aware of a second layer of existence, beyond the mechanistic view of science and technology: a layer which is the underpinning of architecture and which is, also, the basis of our emotional and spiritual relation to the world.

The fact that, like the first method of observation, the second method gives insights about objective truth, in the real structure of the world, is highly significant. It means that aspects of beauty, the nature of life, the deeper aspects of our existence, even perhaps the nature of God, may also become visible truths. And it may also come about that their landscape — like the landscape of modern science — is one that is seen to exist, objectively, and is ultimately available to our inspection. That could be, I believe, the long-term result of the method of observation which I have sketched out here.

It is necessary to understand that there is no choice required between the method of Descartes and the method which I have defined here. The two methods are consistent with one another. In any situation where the relevant facts have to do with things that can be viewed in a machine-like fashion, the method of Descartes is best. Pretend the unknown thing is a machine, and find a model which represents its behavior. But in any situation where the relative wholeness of different systems is the most relevant issue, then the method of Descartes, by itself, will not work. We then need a method which can explicitly, and objectively, recognize the relative degree of wholeness in different systems. In such a case, the method which I have described must be used as well. If we follow both methods — the method of Descartes for things that are outside ourselves and can be represented as machines; and the method I have explained, where we have to study or judge wholeness — we shall then arrive at a picture of the world which includes the self and which is able to recognize the personal nature of the universe.²²

NOTES

1. This example from Akido was given to me by Scott Hunter. I am very grateful to him. There are no doubt many other versions of this test too.

2. This question is, of course, only likely to be successful for an observer who feels that it has a clear meaning.

3. One nicely unassuming and straightforward version, still essentially of the same test, was described by Michael N. Corbett in A BETTER PLACE TO LIVE (Emmaus, Pennsylvania: Rodale Press, 1981): “I became keenly aware of a pleasant feeling and, at that time, realized that architecture should be judged by how people feel when they are using the space for what it is designed for . . .” (p. 113).

4. The following discussion is based on a speech I gave in 1992 in the Dallas City Hall Council Chamber.

5. Later in my visit, I gave this and many other similar examples in the City Council Chamber of Dallas, where there were about a hundred people listening to my speech. Each of these examples was something familiar to them. As I gave each example, I could see people nodding their heads and agreeing. The experiences I described from the streets of Dallas were not unique to me: I picked examples which I knew would be shared by many. I think they were shared by almost everyone listening to me that day. Most people feel their own humanity dimishing when they are in the forecourt of the Dallas Art Museum. Most people feel their humanity rising in the little avenue alongside the art museum.

What we witness here is something, this expanding and diminishing of our humanity, which happens in each one of us. To a large extent, it happens in the same way,

and to the same degree in each of us. Of course, there are still individual differences. Of course, we shall not find perfect agreement about these judgments. But in broad terms, if we observe carefully, with microscopic attention to our own interior feeling, the rising and falling of our humanity from moment to moment, from place to place, we find that we experience this in the same way and largely to the same degree.

6. Taken from the NEW YORK TIMES, February 2, 1999.

7. Thus, what could appear to some readers as a nearly contrived and over-complex definition of value and quality, together with an almost rarified way of deciding its presence or absence, is required by the upside-down character of the present social situation, and the need for us to reestablish a solid foundation for the art of building. It is very practical, very useful, this feeling. It tells me what to do. Those things which make me feel more whole are things to work toward, things to do. The things which make me less wholesome are things to stay away from.

8. These convex segments are the centers that I have identified in chapter 3.

9. Wolfgang Koehler, GESTALT PSYCHOLOGY (New York: Liveright, 1929), and THE PLACE OF VALUE IN A WORLD OF FACTS (New York: Liveright, 1938); Kurt Koffka, PRINCIPLES OF GESTALT PSYCHOLOGY (London: Routledge & Kegan Paul, 1955).

10. This has been very thoroughly explored—as, for instance, in Marian Hubbell Mowatt, “Configurational Properties Considered Good by Naive Subjects,” AMERICAN JOURNAL OF PSYCHOLOGY 53 (1940): 46–69, reprinted in David Beardslee and Michael Wertheimer, eds., READINGS IN PERCEPTION (New York: Van Nostrand, 1958), pp. 171–87.

11. And even this, of course, is susceptible to change. In 1985 the terrace (as shown in chapter 4) was beautiful beyond imagining. In 1997 it was merely nice, with very much less life remaining in it. The son of the previous owner had rebuilt it, and what had once been magical was now merely pleasant because he had altered the centers by remodeling.

12. Experiments of this kind have also been described by Ken Pirsig, in his book ZEN AND THE ART OF MOTORCYCLE MAINTENANCE (New York: Morrow, 1974) where he describes an imaginary (but in part autobiographical) professor of English literature who achieves a drastic change in our way of looking at the world, by establishing empirically that the relative quality of different student essays is a matter of fact, not a matter of opinion.

13. Cristina Piza de Toledo, OBJECTIVE JUDGMENTS OF LIFE IN BUILDINGS (unpublished master’s thesis, University of California, Berkeley, 1974).

14. Hajo Neis has undertaken a wide variety of such experiments, asking subjects to make comparisons of the degree of life or degree of quality in different objects, situations, and artifacts. The results of the experiments, so far unpublished, are available from Professor Hajo Neis, Department of Architecture, University of California, Berkeley.

15. See various studies by Robert Sommer for the effects of windowless rooms on creativity; also bibliography by Educational Facilities Research on the Internet.

16. At the University of California, Berkeley.

17. Alice Coleman, UTOPIA ON TRIAL: VISION AND REALITY IN PLANNED HOUSING (London: Hilary Shipman Ltd., 1985). Coleman used indicators like urine smell in passages and swear words written on walls as negative indicators of wholesome feelings experienced by the inhabitants in these places. The studies had a high degree of statistical reliability, for different features of the environment, which correlated with the presence of these negative indicators.

18. Confucius, THE UNWOBBLING PIVOT, trans. Ezra Pound (London: Peter Owen, 1968).

19. See, for instance, Nina van Gorkom, ABHIDHAMMA IN DAILY LIFE (Bangkok: Dhamma Study Group, 1975), and RUDDHISM IN DAILY LIFE (Bangkok: Dhamma Study Group, 1977), which summarize the main teachings of the Buddhist canon.

20. Frederick S. Perls, GESTALT PSYCHOLOGY VERBATIM (Lafayette, California: Real People Press, 1969). For example, the huge effort which appeared in the years 1960 to 1980 as the human potential movement, included the wisdom that a person will be healthy to the extent that he or she is aware of his or her own inner feeling and can experience and record it accurately.

21. Descartes, MEDITATIONS.

22. This is the subject of Book 4.

CHAPTER TEN: THE IMPACT OF LIVING STRUCTURE ON HUMAN LIFE

INTRODUCTION

To fill out my picture of living structure and its relation with the human self, I shall now examine a supremely practical question, one essential to all of us: What is the impact of living structure on human life?

I have tried to show that the degree of presence of living structure in artifacts and buildings can be judged, and measured, and that it may be measured by estimating the degree of life which people experience in themselves. Thus the living structure of the world is not only real and objective, but also tied inextricably, it seems, to the very nature of our human self.

One can hardly doubt, then, that the physical structure of the world, and especially the world of buildings where we spend most of our time, has a massive effect on us; that our good fortune, our future, our very ability to live, is profoundly tied up with the presence or absence of living structure in the world around us.

In this chapter I shall try to give some idea of how this interaction between buildings and people works, how high the stakes are, and how deeply, indeed, our own daily lives are touched at every waking minute by the living structure of the world.

1 / HOW DOES THE WORLD HAVE ITS EFFECT ON US?

What is the effect on our daily lives of the complex structure that I have characterized as living structure in nature, in buildings, in artifacts?

Common sense tells us—or seems to tell us—that the physical environment affects our lives. It has often been said, certainly, that the shape of buildings affects our ability to live, our well-being, perhaps our behavior. Winston Churchill is believed to have said “we shape our buildings; and they shape us.” But how do they affect us?¹

I shall argue that the geometry of the physical world—its space—has the most profound impact possible on human beings: it has impact on the most important of all human qualities, our inner freedom, or the sense of life each person has. It touches on internal freedom, freedom of the spirit.

I shall argue that the right kind of physical environment, when it has living structure, nourishes freedom of the spirit in human beings. In the wrong kind, lacking living structure, freedom of the spirit can be destroyed or weakened. If I am right, this will suggest that the character of the physical world has impact on possibly the most precious attribute of human existence. It is precisely life—the living structure of the environment—which has this effect.

Those environments which are composed of living centers, which meet the functional conditions described in chapter 7, which meet the extraordinary mirror of the self test, and thus reflect the human self, which do this in accordance with culture and society, and which have the fifteen properties working to support human existence—these places are the ones where we feel most free. Those environments which lack this structure are ones where we feel—and may easily become—dead.

Our emotional freedom, our spirit, is nurtured and supported by those environments which are themselves alive. In an environment which has living structure each of us tends, more easily, to become alive.

2 / FREEDOM OF THE SPIRIT

Can it really be true that something as elusive as freedom — and perhaps the even deeper capacity to be human — depends in some way on the environment? Is it possible that the rude form of walls, windows, and roads could affect something so subtle and precious as the freedom, or the wholeness, of a person?

The effect I suggest is large, but subtle, and resembles the effect of trace elements in the human body. It is well known that various substances — certain vitamins, for example, and to a lesser degree even certain rare metals — have a disproportionate impact on the health of a human body. These substances do not represent a large part of the body's intake, nor are their direct products a large part of the body's biological structure. Nevertheless, they are necessary in tiny quantities, since they make possible the construction of crucial enzymes, which themselves catalyze crucial and highly repetitive components of protein synthesis.

The reason these trace materials are necessary is that they play a catalytic role in various processes. They are used again and again and again in reactions which happen millions of times per day. Without this catalysis, the major and more gross processes of the body simply break down. The impact of the geometry of our environment—its living or not-living structure—has a similar, nearly trace-like effect on our emotional, social, spiritual, and physical well-being.

A healthy human being is able, essentially, to solve problems, to develop, to move toward objects of desire, to contribute to the well-being of others in society, to create value in the world, and to love, to be exhilarated, to enjoy. The capacity to do these many positive things, to do them well, and to do them freely, is natural. It arises by itself. It cannot be created artificially in a person, but it needs to be released, given room. It does need to be supported. It depends, simply,

on the degree to which a person is able to concentrate on these things, not on others. And this steady-mindedness, even in joy, is damaged by the extent to which other unresolved or unresolvable conflicts take up mental and physical space in the person's daily life.

Such damaging interference from extraneous factors can take many forms. It can come about as a result of hunger, starvation, disease, or physical danger — all these, obviously, force a concern that stands above any of the more subtle issues. It can come about as a result of an unhealthy social milieu, such as a dysfunctional family; it can come about as a result of internal unresolved emotional conflicts. So long as these conflicts remain unresolved, not much else can go forward successfully.² Once the larger sources of need and conflict and interference are removed, or taken care of, the more subtle positive life-seeking aspects of the organism take up the challenges, desires, aims, that a person wishes.

More subtle issues can also create such preoccupation, hence damage, to the individual. Conflict in the workplace, for instance, can absorb a person's energy to the near exclusion of all other matters. Personal tragedy does the same, always for at least a short while, sometimes for longer, too. While active, it simply stops a person from functioning well.³ Preoccupation with other matters, with one's own mental illness or neuroses, with family problems, with money problems, with boredom at work, with cruelty, with the well-being of a loved child — all these may dominate while unresolved.

And still more subtle issues, in lesser degree, have the same effect. A chance remark can throw off a person's functioning for a day or two; a badly fitting shoe, a headache, even an irritating noise of motorbikes outside the house can make concentration, productive problem-solving, ultimately creative work, or love, or joy nearly impossible. They take so much energy, so much at-

tention, that it is hard to rise above these problems.

Of course, it is often said that challenge makes us more alive. Climbing a hitherto unclimbable mountain, solving a problem at home, finding a way around a difficulty, running along the edge of the sea where it is hard to run in the shallow water—all these are exhilarating. They make us more alive. The artist starving in his garret is more likely (it is said) to create the great work than one who is pampered and supported. Orville and Wilbur Wright refused a grant because they felt that too much money would destroy their ingenuity in the face of necessity—the very factor which they both treasured most dearly in their search for a flying machine.

The nature of the interference caused by hardship and conflict must therefore be very well understood, and accurately gauged, before we can say that we have a clear picture of its effects—either negative or positive.

3 / FREEDOM AND LOSS OF FREEDOM

Let us now come to the topic of human freedom. It will be accepted, I think, that the best environment would be one in which each person can become as alive as possible—that is as vibrant intellectually, physically, morally—and in which people can reach, as far as possible, their own potential as human beings. One may assume, too, that each person naturally does everything possible, to be alive. The tendency to enjoy life, seek life, live life to the fullest, is a natural human force. It is the thing a person most naturally aspires to, and seeks.

The psychologist Max Wertheimer once wrote a short article called "A Story of Three Days," in which he proposed a simple, and extraordinary definition of freedom. In his article, Wertheimer describes a man who is searching for a definition of freedom. What is freedom? What is true freedom? he asks again and again throughout the story. In an effort to find a satisfactory answer, he continually proposes possible answers, by a kind of self-imposed Socratic dialogue, and then visits people and places to see if the answer is correct.

At one moment, for example, he contemplates a man in prison, someone who is caged behind bars, yet nevertheless extraordinarily free as a human being. Clearly, he argues, it is not the absence of bars, then, which defines freedom.

Nor is it the restriction of the bars, the incarceration in and of itself, that causes the loss of freedom. So he goes on to propose another hypothesis, and visits other places and people and situations.

This searching, in Wertheimer's allegorical story, goes on for three days. Finally, at the very end, and having by-passed all the obvious definitions of freedom, having exhausted all the other definitions he can think of, Wertheimer's protagonist concludes that true freedom lies in the ability a person has to react appropriately to any given circumstance. The perfectly free human being is a person who, no matter what she or he encounters, can act appropriately.

And what is lack of freedom? Anything which causes a blockage of this ability to react appropriately—whether it be internal obsessions or mental rigidity, or a political system, or the bars of a cage—causes a loss of freedom. Lack of freedom is loss, from whatever source, internal or external, of the ability to act appropriately.

We see here, how the environment can cause loss of freedom. A company which forces top administrators to deal inappropriately with human conditions that arise among the staff is reducing freedom. A building which creates so many small stresses in ordinary matters that people

cannot pay attention to what needs to be done, also reduces freedom. So does an environment which encourages a person to think obsessively about the image of the environment, while ignoring everyday feelings and practical realities.

Various conditions exist on earth in every human society which constrain people, which reduce their freedom, make it more difficult to live life to the fullest. A great number of these conditions come from the environment and its physical structure.

Let us consider an architectural example of interference with freedom. Illustrated on this page is a housing project in which the parking lot leads directly to the houses. (This structure is in Fort Lauderdale, Florida, but could be almost anywhere in the world today.) It creates conditions which make it hard for people to react ap

propriately to their living experience. There is no common land and therefore no real opportunity for people to experience any sharing or public or common interaction. The desire for this kind of interaction may well be slight. But when it occurs, as a natural impulse, it cannot be satisfied—indeed it is prevented, frustrated, forces run underground, natural expression of action is modified and curtailed.

Consider the same housing project from another point of view. Families cannot express their individuality. Each family is different. But shut into a box that makes allowance only for the most gross physical functions (cooking, sleeping, using the bathroom), the opportunity for the individual to grow is reduced, curtailed.

In both ways, this housing project undermines and interferes with freedom.

4 / THE STRESS RESERVOIR

We shall understand the negative effect of environment on human freedom more deeply by considering the phenomenon of stress.

Broadly speaking, the reaction to each unsolved problem, or annoyance, or conflict that is encountered creates in the individual some level of stress. Stress is initially functional and productive. Its purpose is to mobilize the body in such a way that problems get solved. Adrenaline and other agents are mobilized throughout the system, creating special alertness and energy. All these help to address conflicts, unwind them, and to remove sources of annoyance. Each conflict or difficulty that the organism encounters, so long as it remains unsolved, adds to the stress that is mobilized. But there is a limited capacity for stress in every human individual. Varying from person to person, it is nevertheless quite finite in all of us.

There is, in effect, a stress reservoir in the body. The amount of stress being coped with fills

this reservoir, to different levels at different times. But as the stress reaches the top of the reservoir, the organism's ability to deal effectively with the stress decreases. This then gives rise to the "stress," as used in its popular meaning. The organism is overloaded. There are more problems occurring than can be solved. The total stress mobilized is beyond what the organism can cope with effectively. Slowly the situation deteriorates. When the stress is too great, creative functioning is impaired. Sometimes it finally breaks down altogether.

Perhaps the most important finding of modern research on stress is that this stress is cumulative, because it is all in one currency. Stress from money worries, stress from physical pain, stress from an unresolved argument, stress from light shining in one's eyes — it is all stress, and it is all one kind of stress. So each of these apparently disparate stress effects fills the same stress reservoir.

Almost any unresolved problem, even when small, adds to the reservoir of stress, and can reduce a person's ability to function well. So long as challenges faced are within the limits of the stress reservoir, a person is actively solving problems, and becomes more alive, more capable, more rewarded in the process of meeting the challenges. When the stress reservoir fills to impossible levels, the effect is opposite, and the accumulated stress prevents productivity, prevents loving relationships, prevents artistic and intellectual creativity, prevents people from being effective.

To see more exactly how the accumulation of stress, and disruption of the healthy relation between living structure in the environment and human freedom works, look at the case of a wall outside the University Art Museum in Berkeley, California. This wall has sloping sides, unlike a normal wall which has straight sides. Both ground surface and wall are made of concrete, and the concrete slopes and curves continuously from the flat ground to the vertical surface of the wall to form the wall. I suppose the architect

thought this would be fun, or exciting — or perhaps just “different.” But what it actually does is to create very tiny amounts of stress. A person walking along cannot quite tell where the sloping part starts, so there is a chance of tripping. One has to walk away from the wall, minding one’s feet, and has to give up what one is thinking in order to concentrate on not bumping into the wall. And if you were inclined to sit on the wall, you could not. The top of it is too far back from the flat part of the ground; your legs don’t quite reach. So this wall, apparently fun and interesting, is actually a little expensive in needless stress, and in discomfort. This could have been avoided by an ordinary wall 16 inches high, thick enough to sit on, with a wide top, where you can see what it is when you walk by, and where you can sit down if you are tired, wait for a friend, or have a sandwich.

Of course, this example is small scale. Human life would be easy if we only had a few problems of this kind to contend with. It seems almost petty to mention it; perhaps too critical of the architect who was, conceivably, just having fun.

Let us now consider a rather more troublesome example from architecture. This concerns the life of families with small children on the fifth or sixth floor, or higher, in apartment buildings. The problem has been well documented: the mother with small children; the apartment usually small. Naturally the children—when they are home—want to go out to play with their friends, on the ground, six stories below. The mother wants them to be able to play there. But she cannot easily keep an eye on them, and she can't get to them quickly if something happens. But she can't keep them in the apartment, which is too small anyway. So the children go down. She worries constantly, thinking perhaps about kidnapping, or a car accident. But there is no alternative. If she finds it too stressful, she keeps them in the apartment, but after an hour of children romping about breaking things in the apartment, which is too small to contain many friends, she gives up and goes back to the inevitable. She lives with this stress day in, day out. If she tries to go down to watch the children, from the ground, then the cooking doesn't get done, and all kinds of other negative consequences come from it. There is no way to win. One way or another, this condition remains in her for the few years when her children are young enough to need supervision, but not young enough to keep at home. This stress cycle contains a series of factors linked in a "can't-win" pattern. It is just one example of a negatively charged system of conflicting forces which occurs in certain kinds of apartments: one of the many other things that might be said about not very good apartment buildings.

But the main point is that here we have a second example, in structure like that of the museum wall, of a system which absorbs energy and makes living more difficult, and thus interferes with a positive development of people's lives. This example is somewhat larger in scope and in its effects than the art museum wall. The nature of the stress that is induced is the same.

Each example adds to the total reservoir of stress people must contend with. It makes everything else more difficult, and a meaningful life just that little bit harder to attain. By themselves, the stress from these two cases could not fill up a person's stress reservoir. But when these small items increase, and multiply, they begin to have a cumulative effect which is not positive, but negative.

It is in the subtle interplay of factors of this kind that the environment has its effect—positive or negative—on human life.

5 / SEPARATION FROM REALITY

The further the stress reservoir is brought to overflowing, the more people are surrounded by conflicts which make it impossible for them to meet their ordinary striving and aspirations. They struggle, but are undermined continuously by a separation from every reality, and by a separation from the experience of solving problems, overcoming them, and meeting challenges and overcoming them, and becoming, therefore, free.[6]

So the apparently small trace-like conflicts in the environment all cause stress. But they go much further. They cause a separation of people from reality: they form a world, so removed from everyday human events, that it might almost be said that it is made for fictitious people to live there at all.

Thirty years ago, the film-maker Jean-Luc Godard made a science horror film, ALPHAVILLE, in which he tried to convey the deadness and nearly horrific stillness of an imaginary coming world, where people behave almost like robots. Opposite is a real building, built by Terry Farrell, which achieves this quality in a building now standing on the River Thames, in London. On

An environment—not from horror film, but from real life, on the south bank of the Thames, in London. This can hardly create anything but a shudder of apprehension, deep down. Certainly it is not a nurturing environment which allows one to be oneself, or to be free.

page 376 there are high-rise apartment buildings crowded together in Naples. And a more recent realistic film DIARY OF A POOR YOUNG MAN, by Ettore Scola,⁸ where a young man is slowly annihilated by the oppressive environment of a massive repetitive public housing project.

In each case, one reacts with a certain horror. The inhumanity of the environment, and the inhumanity it causes in us, are not imagined, not literary fictions. We easily re-create, in our hearts, the sense of hopelessness and despair, the confining reality of a sterile world, that are summarized by these illustrations. We can feel it in ourselves. And we know, from our own walks through the empty office building, through the still, despairing upstairs mall of shops, or through the empty motel room, devoid of all but bed and bathroom and small window and plywood door, how real this despair can be, and how little this atmosphere does to sustain us — how, rather, it can bring us nearly to the brink of hopelessness.

6 / A WORLD WHICH ENHANCES HUMAN LIFE

Using Wertheimer’s definition of freedom, we may define the best environment for human life. It would be one which gives people the maximum chance to be free, one which actually allows them to be free. A living environment is one which encourages, allows, each person to react appropriately to what happens, hence to be free, hence to encourage the most fruitful development in each person. This is an environment which goes as far as possible in allowing people’s tendencies, their inner forces, to run loose, so that they can take care, by themselves, of their own development. It is an environment in which a person is free to grow, if she wishes to grow, and to do so where, and how, she chooses.

This environment will be, by character and in structure, something far less ordered in the superficial sense than we architects may imagine. It will be more rambling, with a deeper kind of order than we have come to expect from our profession, something more like the rock pool with its hundreds of species, a subtle biological order containing vast structure, but seeming, on the surface and geometrically, almost disorderly.

It has just that structure which I have described, throughout this book, as living structure. It is a highly complex system of centers, like those in nature, which support each other, and where each part, in itself, is alive.

This environment releases you, allows you to be yourself, allows you to be free. Ease. The yawn, a smile, a perfect ease which allows you, above all, to be yourself, to provide that part of social existence which also protects and heals the self.

This ease, this freedom, depends on configurations which are opposite from the conflict-inducing, stress-inducing configurations I have been describing earlier. Rather it depends in part on “opposite” configurations, those which remove energy-wasting conflict from the environment. These “opposite” configurations release human effort for more challenging tasks, for the freedom to be human.

The 253 configurations in A PATTERN LANGUAGE are of this type.⁹ Each pattern, when examined carefully, describes some conflict — better said, some system of conflicting forces — which will arise in the wrong sort of environment, but which can be tamed, resolved, when the environment is right. LIGHT ON TWO SIDES OF EVERY ROOM, FOR EXAMPLE, describes a situation in a room with light coming from one side only, where the light is not reflecting enough, where people cannot see one another’s faces well enough, and where deep stresses will remain. In this case, again, the structure is not easily changed. Only an increased wisdom, which

avoids building one-sided structures, or makes rooms shallow enough to allow the light to bounce correctly, will solve the problem.

INDEPENDENT REGIONS describes a situation in a large nation state, where local regions—for climatic and cultural reasons—have their own identity, but where this identity is trampled and disturbed when the nation state is too powerful. The pattern (described in 1970, when giant nation states were common, and small countries less common) was so powerful that the forces in tension began to have major historical and political effects, eventually culminating in the breakup of the Soviet Union and Yugoslavia and the creation of small independent countries throughout Africa and eastern Europe and the Indian continent. The conflicting forces, in this instance, can be more easily resolved within the configuration of small countries, and political force and political wisdom therefore move the world in that direction, to permit the autonomy of individual cultural identity.

In both cases, so long as the configuration is wrong, the conflict remains underground. Yet there is no benefit to keeping the conflict under the surface. All that does is add to stress. It does not contribute challenge. It is, in any case, invisible, experienced only in the built-up stress, not as a creative challenge.

Some people thought that a PATTERN LANGUAGE was written to recreate a nostalgic atmosphere, since so many of the patterns resemble things "as they used to be." In fact, the content is far more practical. The patterns describe 253 of the most common subtly conflicting systems of forces which can occur in the human environment, and show what configurations will eliminate the stress cycle, release people's natural force, and thus make room for positive forces, positive emotions, and positive human interactions to have free play.

A world in which these patterns and others like them are present, thus tends to support human beings in their efforts, in their striving for life, in their search for happiness.

In an alcove of the Linz cafe

7 / ANDRÉ KERTÉSZ'S PARIS

Look at the pictures of Paris on the next several pages.¹⁰ These pictures describe a world in which life is being realized fully.

It is not a stress-free world. On the contrary, many of these photographs (all taken by André Kertész in Paris, around 1930) show people struggling with poverty, with crippling difficulties, with constraint, with problems that might — even today — be considered overwhelming.

Yet there is a freedom visible in these pictures. Life is being lived deeply. These people, no matter their stresses and difficulties, are free, somehow free in themselves. And this is recognizable. That is why we view André Kertész as a great photographer, and why the world captured in his pictures tells us something of the greatest importance about our lives.

What does it mean to say that these people in Kertész's pictures are free? And what does it mean to say that the environment supports them in their desire to be free?

For I do mean to say that the physical world shown in these pictures supports these people, and that it is because of this world, and the way it interacts with them, that they are free.

I think it is fair to say that what makes the Paris of these pictures a great place, a sustaining place, is the depth of the life which it releases. But this freedom is intellectually puzzling. Since these people are evidently struggling with great stress — ill health, hunger, poverty, squalor, unkindness, loneliness — we need to understand the nature of this interaction.

A caged bird on the rooftops is placed so that it allows the bird to see the sky. The dancers gather. The old man lays his artificial leg on the table, and shuts one eye. Stragglers look for leavings as dawn comes to the Seine's banks. Children gape, passionately, at the Punch and Judy

show. The old lady walks her cats across the road. A man on a balcony catches the last glimmer of afternoon light, in his shirtsleeves, with his newspaper. The flower seller, legless, fails to catch the young woman's attention as she hurries past. Lovers look out from their small window. The old lady peers at the prints in the print shop along the riverbank. The river flows; leaves fall; dust settles. Fishermen wait in silence in the early morning. Somewhere else the traffic roars. A woman washes her clothes.

It is obvious that these experiences shown in Kertész's pictures are profound examples of life. We know it just from looking at the pictures. The pictures are at once happy and sad. They have in them the full reality of life. It is neither fully pleasant nor wholly unpleasant. Certainly it is not pampered, or conflict-free. It just is. Remembering the death that is to come, knowing that at that moment life was lived, these are records of experiences in which that fact of life is experienced to the most extreme.

How is freedom encouraged or supported by the environment? What is it about these archaic, not refined, rather rough pictures of Paris, with living structure, that supports freedom, allows people to be free?

Simply put, many of the energy-draining conflicts or stress cycles that could happen have been removed. What exists in these places is something in balance, cleaned from extraneous stress, rather as a meadow of grass is free from stress cycles.

In what sense then are these living experiences also centers or caused by centers? Look at the woman doing the laundry in her attic (page 390). It is not a wonderful attic. It is not a dream laundry. Her work is hard, not soft. So why does this picture convey such substance? Because the washing of the clothes is part of the attic, part of the roof, part of the structure of the house. The wholeness of life is experienced. And this occurs because that washboard, the sink, fit awkwardly into an otherwise unused corner. There is no waste, nor money available for waste. Hard, dour as it is, it is complete.

The fishermen at early morning water, the Seine without ripples: How is that related in any way to living centers? Each fisherman, as a center, takes up his position, and these centers of the men and their rods are part of the larger scene, each center helping the others which are there.

Can this be created? Can the intense life, lived in these moments which André Kertész recorded, be designed-in, incorporated, intentionally built into the world? Can architecture go that far?

I think it can. The physical world, its wholeness, enters into these events very specifically in the following way: each of these situations is marked by a structure which leaves itself alone. What happens there can happen because what is there is only the essential of the world. There is no superfluous structure. It is easy. It feels relaxed, life-extreme, because there is no dross, no developer's trademarks, no attempt to sell the buyer, no room for extras which are not real. It is the purity of the Paris scene which allows these forms of life.

This paring away of non-essential centers, the filtering out of extras, leaving only the essential centers there, can be created in a physical world which has only the essentials in it, and deliberately avoids all physical centers which are not absolutely required.

This spirit is hard to attain. Perhaps it has always been hard, for all human beings, at all times in history. It is, perhaps, especially hard in our time. We have a world in which some live in poverty, not even having the bare essentials, while those who have more money generally have far beyond the bare essentials. A world made of essentials is unfamiliar to us. It does not exist in poverty; it does not exist in luxury. It does not exist in the vast acres of middle-class well-designed convenience.

But still, the presence or absence of this necessary atmosphere is embedded—or not—in the physical world. What is needed to allow these events is a structure whose wholeness is pure, empty, has nothing in it except the barest. This is not at all a structure which is missing. It

is a very specific structure which must be present. If the edge of a river is furnished with public picnic tables, this may make the picnics easier. But it does not help the bare bones of existence flourish. The freeway along the river's edge does not help this communion between man, woman, and water. The expensive restaurant creating valuable real estate for the business lunch or dinner will not, also, allow these essentials to occur.

It is easy to see from such negative examples, as from the positive settings of Kertész's pictures, that the geometry of space has an enormous role to play in the presence or absence of deep human life: the centers in the space either support, or hinder, the evolution of free life. Consider Kertész's bench with the old ladies talking. The wholeness of the bench includes the way the sun falls on it, the fact that it is sheltered from the wind, the people sitting on it, children playing behind it. These are all centers. All of them,

though in the realm of what we usually call "actions," can still be understood geometrically as part of the hierarchy of centers which are relatively more whole or more intense. But we now understand this wholeness to include centers which grow and fade as life goes on during the dynamic minute-to-minute actions and events which are occurring there. This new wholeness (which includes centers that are events) may still be sustained or not by other centers within the system. For example, it may be sustained by a gap in the buildings to the south which allows sunlight to fall on the bench. It may be sustained by the slope in the back of the bench which increases the comfort of the seat as people actually sit.

The wholeness may also be sustained by centers that are pure actions. For instance, if the bench is close to a path where people walk and wheel their children, this movement can sustain

the wholeness of the bench. If the flowers on the trees attract birds, and the singing of the birds then intensifies the beauty of the bench, the birds contribute directly to the wholeness of the bench. The flowers may contribute indirectly, by con

tributing to the wholeness of the bird-filled trees. Thus the wholeness is a complex living structure: it may be sustained, or not, by countless aspects of the various systems which surround and fill the space where the wholeness occurs.

8 / THE MIRROR OF THE SELF

If we ask how this environment in Paris works to help people be free in themselves, the answer lies in the living structure. Again and again, a living world contains living centers, and we see them, feel them, experience them, are surrounded by them, bathed in them. Strong centers, boundaries, roughness, alternating repetition — all create living centers, and they do it in a way that makes things work. But, in addition, there is a factor which is large and overwhelming. It has to do with the strong nurturing sensation that occurs in that environment. Said simply, we feel

overwhelmingly, deeply, comfortable in the structure of that Paris which Kertész photographed.

What is this nurturing sensation? It can still be felt today, in those places depicted. But where does it come from? Over and above the functional patterns, and the presence of living centers, the answer is given, by the findings of chapters 8 and 9. What we see, in Kertész's photographs, is a profound version of the living structure, so made that it—very deeply—connects us with ourselves. That is where its comfort

comes from: it supports us in our souls. If I want to say the same thing more formally, more empirically, I can say the places which are visible in Kertész's pictures are very strong on the mirror-of-the-self test.

In effect, then, these people in the photographs—no matter what miseries, what struggles, what human problems they experience—are nevertheless bathed in Self, they are surrounded by it, surrounded and sustained by a world in which every particle, each stone, each sidewalk, every door and window, reminds them of their own self, affirms the existence of their own self. And that is, of course, precisely the same living structure which will fare best on the mirror-of-the-self test. It is just this sort of thing, beautiful and rough, which most reminds us of our true self, the self which is sorrowful and happy, trivial and deep.

There can hardly be a greater form of sustenance. It is not surprising then, that this enrichment, allows people, to find the strength in themselves, so that they may also be free. In this fashion, I believe that the self-like character of the environment has a direct impact on us, it nourishes us, it supports us. And in this way, it provides us with a certain freedom and ability to be free.

One feels that in the Parisian environment of Kertész's time, people are grappling with real problems: a lost limb, no work, too little food. The stressed and hopeless people in the not-nurturing motel or in the empty shopping mall of more recent times—they are not suffering from a real problem, more from a lack of engagement, a loss of connection to the earth, to their fellow creatures, even to themselves.

Life in that Paris is rough. It is hard. But it does not impose the lethal disembodiment of the human being, which the pictures on the previous pages portray, and which those buildings implement.

The photographs by Kertész are great photographs precisely because they remind us of just such a world, where life is real, challenges are endless, yet luxury, even in a puff of a cigarette

on the river embankment, can be treasured just because it is so brief.

That is the environment which is most able to support the inner life, and which will, in the end, do the most to support life as most of us hope to live it. It is an environment which does the most to support true life, equally in the depths of our despair and in the course of the most happy love affair. The dirt assembles, the rocks tumble, and the wild rose blooms in the crack between two bits of concrete.

But these issues are still not simple; they should not be oversimplified.

Let us go over the ground again. Human beings differ in their strength, in their freedom of spirit, in their ability to be free. Nelson Mandela was in prison for twenty-five years, and his spirit did not crack, his inner freedom sustained him throughout it all. One could hardly imagine a less nurturing environment than the bars of his cage, or the quarries of South African stone-breaking gangs to which he was chained. But he remained free, perhaps became more free during his experience.

Another person, at the opposite end of the scale, may be unfree, obsessed by guilt, or inner conflict, or lack of will, and may thus be miserable, even in the most nurturing environment.

So, you may say, what then is the connection? In what sense can one say that the environment helps us to become free, or hinders us from becoming free?

What we may accept, I think, is that the environment has the capacity to nurture. The origin of this capacity—and the impact of the environment, of living structure on ourselves—are more complex, and deeper, than the mechanical analysis of stress can quite encompass.

The connection hinges simply on the fact that as one center is lifted, made more alive, by the sustaining quality of other living centers, so we, too, being living centers, are sustained, uplifted, made more alive, by the presence of other living centers.

It, in the end, is as simple—and as profound—as that.

10 / EXPERIMENTS IN OUR TIME

Can we aspire to this? To Kertész's pictures? Can we aspire to that atmosphere now? Is it even possible for us to create such an atmosphere, and to create this loving, even when somber, relation of ourselves to our environment?

This is a vital question. Analysis of the freedom that is evident in the Kertész pictures would be a little empty if there was no hope that we ourselves might reproduce it, create another version of it in our time.

Until a few years ago, it would not have occurred to me that this might be possible, or that we might aspire to it. But almost as an accident, I began to find out that things that I was myself building, when I was trying to create the kind of living structure described in this book, had such an effect on people.

If I had not had that experience it would not

even have occurred to me to write this chapter. The first time that it happened was in Mexicali, where I built low-cost housing for some Mexican families. The techniques I used to build the project were closely related to the theory I have put before you in this book, and to the processes described in Books 2 and 3. The family members themselves played a big part in planning and building these houses. And then, after the families moved into the houses, one of the family members (José Tapia) said to me:

Well, I have not specifically noticed any effect of the project on my work, or my attitude toward society—but I have noticed that I now do quite different things at home from what I used to do in our old house. In our old house, when I came home from work, we used to go the mov-

ies, go to the bar, things like that, in our spare time, more or less just to kill time. Now, because I like it here, and feel so good here in this house, because it suits me so well, I have suddenly realized that there are all sorts of other things to do. I can make something. I can talk to my wife about what we can do to improve the house, or do something with my brother in the yard outside... so it has changed me personally; it has changed my personal life, I feel more potent in myself, not in relation to society, but in relation to the small things I do every day, when I am in the home, and when I come home from work.[11]

I knew, in Mexicali, that I was trying to capture, in some way, the essence of traditional architecture — what made buildings live. But until that day, talking with José, I had not realized that once one achieved the life of the architecture, people would then feel liberated, in some literal fashion, and that their lives would change because of it.

I heard a similar response after building the Eishin campus, a high-school and college campus I built in Saitama province, west of Tokyo, Japan, in 1985. My clients thanked me, at the end, not for the beauty of the buildings, which was sometimes also mentioned, but because I "had helped them find the new way of life that they had been hoping for."

I heard it again in Ann Medlock's poem, where she thanked me for the house I built for her and her husband on Whidbey Island in Seattle, Washington:12

Feasting on tabouli and cold birds, we talk of poetry and paintings, of terraces in Tuscany and home-made wine, of our work, our passions, our quests. We are friends, gathered here by the grace that emanates from this holy place.

It is lacking in humility for me to recount these stories. I apologize for that. But it is necessary for me to describe these cases. It was only after I realized that some of my buildings had

these effects on people that I began to understand that the new architecture I was groping toward had an even more profound root than I had imagined.

I first built these kinds of buildings, originally, because I believed, instinctively, that it was the right thing to do. I gave them living structure as best I could. It was extremely hard to do. But as I began to succeed in it, and these qualities were actually reached, I found, then, that people were affected in their inner freedom—as if something that had tied them up had been loosened, and as if, in the presence of these buildings, they were more honestly able to be themselves, to be what they wanted to be.

If I had not had these experiences and then seen, many times, that people had these feelings, and described them, it would not have occurred to me to draw the connection—the causal connection—that I have tried to explain in this chapter. Indeed, I think, it would not even have occurred to me that Kertész's Paris influenced people, supported them, actually gave them life—and that this life, which was attained

there, is attainable for us, concrete, and can be aspired to, and created.[13]

That is, perhaps, where my conviction about the subject, and my effort to write these books, consolidated itself. People's experiences in the places I have built gradually made me understand that it is possible for us to build a world in which people are emotionally free, fully themselves, alive, extant in their own reality.

Occasionally, in these places, people seem to feel their own freedom more sharply. The character of the world, its geometry, is so closely tied to them—to their pains, their breath, their thoughts—that it makes them free in themselves, allows them to act appropriately. It gives them the environment which supports them in their freedom.

We may conclude that this kind of geometry, this kind of world—wherever it occurs—creates a slightly greater chance that each person is enabled, made more free in thought and action, and is given encouragement and liberty to live as that person really wants to live—by the existence of the living structure all around.

11 / “FOR THE FIRST TIME I WAS FREE”

I should like to add two other bits of evidence which suggest that the liberation of the human spirit may be connected with the contemporary creation of living structure. Both come from the Eishin campus in Tokyo, which my colleagues and I built for the Eishin school in 1985.

On December 7, 1991, the fiftieth anniversary of the attack on Pearl Harbor, as a memorial and as a healing tribute, NHK (the Japanese National Television company) had a one-hour program showing five examples of Japanese-American cooperation since 1945.[14] One of the five was about the Eishin campus. They showed pictures, had interviews with Hisae Hosoi, the managing director of the school, with teachers, and with students who discussed the life of the campus as it had become.

One of the high points of the program remains etched in my memory. The director of the program was interviewing a young man, a student at the school. He was an art student, eighteen or nineteen years old, dressed in black from head to toe, with something of a punk look about him. He had left his class to give this interview, and he and the film's director were talking behind one of the buildings, so that he would not be called back to class.

The interviewer asked him what the campus meant to him. He thought for a long moment, then answered quietly: "I grew up in Tokyo. All my life I did not know what to do, or who I was. All those years of growing up, I felt I was in prison... I never could get out of that prison..."

He paused. Then staring straight into the camera, he said, "When I came to Higashino, to this campus..." He paused again. Then, looking softly, even more intently, into the camera's eye, he said,

"For the first time in my life, I felt that I was free."

After saying that, he was silent.

12 / THE JUMPING-IN-THE-WATER FILM

Ten million viewers watched this young man make that statement in that quiet way. I have always felt shocked by his statement, and yet in some kind of wonderment, thinking about both what he said and how he said it. The intensity of his expression stays with me. So do the words themselves, what he said.

There was another event, also on that campus.

When we began the Eishin project, I had asked teachers in the old school (in Musashinoshi) what they thought about the life of the new school, what would make them happy, what would make them be themselves. At first, many did not want to speak about it. They assumed that a high school had to be an asphalt jungle, a big block in the middle of an asphalt playground. What point is there in discussing it?

But I persisted. I told them that I understood the frustration, but that our purpose was to do something which really went to the heart of their dream. One by one, to each of them, I asked, “Please close your eyes, imagine a most wonderful place where you could dream of being a teacher. Imagine that you are in a place which is perfect, the most wonderful school that you can

imagine. You are walking about there. . . . Now, keep your eyes closed, imagine yourself walking about there. What, then, do you see. What is it like, where you are walking?"

I was surprised that many of the teachers, in answer to this question, said to me something along these lines, "It is a place like this . . . I am walking along by a stream, quietly thinking, preparing my classes, thinking about my next lesson. It is quiet. I can walk quietly along in such a place."

Another said that she was walking by a pond. Another spoke of a river and a lake. Again and again, water appeared in their descriptions. So, indeed, when it came time to plan the campus, we did include patterns describing this water—a lake, in particular. And then, when we actually made the site plan, we made the low swampy area in the middle of the site, into a lake.

In 1989, several years later, the students were living and working there. On the occasion of an annual festival, some of these students made a film, a low-budget surrealistic film about the school. It was eight minutes long.

The film began showing many students running about the streets of Tokyo, parched, like

dogs, their tongues are hanging out, they run up and down the streets, always parched, panting, their tongues hanging out, like hot and tired dogs. After a minute or two showing this kind of thing, the film showed the students coming to the campus. They arrive at the main gate, and gaze in, as if into a paradise. They run in, down the entrance street, one by one, all running in. As they approach the lake, they see it ahead of them, but they do not hesitate. They run toward the lake, and one after the other, they jump in, clothes and all.

Joyfully they swim about, oblivious to their clothes.

The film ends.

I have often thought about that film. It is true, that when one asks the students, or the staff, what they like most about the school, it is the lake. So it started with the initial feelings, which they expressed at the time of our making the pattern language: the desire to walk by a stream, quietly composing their thoughts. Then came the construction of the lake. Then came the feeling about the lake as the most important thing. Then came the surrealist film, made by students, trying to express their feeling for the place, jumping, fully clothed, into the water.

I experienced all this in the students' film, as a kind of hymn to freedom. The real feeling in a person is at last released. It is expressed, the dream is allowed to become real; the dream is fully realized. The dream, their freedom, the capacity to experience that fresh water, the freedom of the soul, are all made actual.

Interestingly, in 1989, the same year that the students made this film, some of them also made, spontaneously, a poster, expressing their feeling about the school. I came across it in a classroom where I had not been before. Somehow, wherever they went, the school made them experience their own freedom.

13 / ORDINARY REALITY

Hosoi told me once that one of the remarkable things about the school, in his eyes, was the fact that boys and girls could go to secret places, be alone, be untroubled, unwatched. "They feel at home there, these students," he told me.

He was criticized by other school administrators for making this observation, but he defended it strongly, saying that the experience of real freedom was something infinitely more precious, and more important, in the educational process than adherence to the watchful eye of teachers and parents.

This freedom that the Japanese students felt in the school, and feel to this day—the freedom that José Tapia felt in his house, the freedom that Ann Medlock felt in her house—comes, in each case, from the physical layout. It comes, in part, from the actual freedom which is realized because of the real unfolding process that made the plan in relation to the land. The fact that what

has happened is true — real, coming just from the symmetries of space, from the ordinary reality of the world — this has a free breath in it, very much as the rippling sand dunes have because they arise from the same process. We recognize the freedom of the forces, liberated by the unfolding process, and we can breathe more

deeply there. And the freedom in people comes also — at least in part — because the space, both buildings and exterior space, has something approaching an archetypal character that goes so deep inside our own stomachs that, once we experience it in a real place around us, it connects us to ourselves.[15]

NOTES

1. During the mid-20th century, several investigators began trying to pin this question down, and to find out what kinds of causation linked our lives to the structure of the environment. It proved extremely difficult to find the nature of this linkage. These studies are reviewed in Constance Perin, WITH MAN IN MIND (Cambridge: M.I.T. Press, 1970); Harold Proshansky, William Ittleson, and Leanne Rivlin, eds., ENVIRONMENTAL PSYCHOLOGY: PEOPLE AND THEIR SETTINGS (New York: Holt, Rinehart and Winston, 1970); Robert Gutman, ed., PEOPLE AND BUILDINGS (New York: Basic Books, 1972).

A classic example of the difficulty was the attempt to find a negative correlation between density of neighborhoods (a physical pattern) and social indicators of mental health. The assumption was that in overcrowded and high density living conditions, people's mental health would be damaged, lower, on average. For rats, for instance, such correlation does exist between overcrowding and organic damage and mortality. Although it seemed "obvious" that there must be such a linkage for human beings, too, in fact this "obvious" point turned out to be wrong. In one classic study, the most positive mental

and social health occurred in a very high-density neighborhood — Boston's North End. The reason was that the area was, at that time, a mainly Italian neighborhood. Italian family and neighborhood coherence was extremely high, and mental health was found to be better than in comparable areas of lower density. Similar results were found in Chinese neighborhoods, also marked by strong family cohesion. But the mental health and social health came mainly from the social structure and culture, not from any direct link with the physical environment (See Robert C. Schmitt, "Density, Health and Social Disorganization," AIP JOURNAL 32 (1966), 38-40). This underlines the point by showing how hard it is to find a pure and direct linkage between physical structure and human well-being. It draws attention, too, to the dangers of looking for a connection which is too simple-minded.

This sort of muddle led some social scientists to conclude, in broad terms, that the physical environment, when taken by itself, has few directly causative effects on human life. Common sense tells us that there is some sort of effect. But no one quite knows how to characterize the effect. This odd episode in the intellectual efforts of psy

chologists and sociologists occurred because they were looking, in all likelihood, for something too simple. They were, perhaps, asking the question: can a physical configuration of the environment cause—that is, induce—a particular kind of behavior in human beings? For instance, can an environment make people mentally healthy, can it make them friendly, can it make them studious, can it make them helpful, can it make them aggressive or passive, can it make them happy or sad?

It is not surprising that this question was, by and large, answered in the negative. With benefit of hindsight, it seems obvious that one would hardly expect to find such a simple kind of connection. Human behavior is so much more complex. People, by and large, are autonomous creatures. They will do what they want to do. Further, social behavior, culture, and human rules of behavior mediate the interaction, and enter in, somehow, into almost every human event. A building cannot, therefore, by its shape, force a person to do something against his will.

But of course the conclusion that was sometimes drawn—namely, that the shape of buildings does not matter—was far, far from correct. The search for a too-direct effect had trivialized the question, and hence the answer. Such a direct effect in human-environment interactions is not what we could reasonably expect to find. But the effect which does exist is, I believe, truly enormous.

2. Abraham Maslow, TOWARDS A PSYCHOLOGY OF BEING (New York: Van Nostrand, 1968). Maslow's discussion of self-actualization gives a rough account of this process.

3. Alexander H. Leighton, MY NAME IS LEGION. Volume I of THE STIRLING COUNTY STUDY OF PSYCHIATRIC DISORDER AND SOCIO-CULTURAL ENVIRONMENT: FOUNDATIONS FOR A THEORY OF MAN IN RELATION TO CULTURE (New York: Basic Books, 1959), especially pp. 133-78, (1) A given personality exists more or less continuously throughout life in the act of striving and (2) Interference with that striving has consequences which in turn often lead to psychiatric disorder. (p. 136)

4. Max Wertheimer, "A Story of Three Days," in Ruth Nanda Anshen, ed., FREEDOM: ITS MEANING (New York: Harcourt Brace, 1940), pp. 52-64.

5. Stress, and the stress reservoir model I summarize here, has been studied extensively, by Hans Selye and others. Hans Selye, THE STRESS OF LIFE (New York: McGraw-Hill, 1984).

6. The loss of connection to reality which occurs in a disordered environment is well-known and discussed by many psychiatrists. Architects have been slower to recognize their role in this process. One example of a failure to recognize such a role appears in the argument made by Peter Eisenman in the Alexander-Eisenman debate, "Discord Over Harmony in Architecture: The Eisenman/Alexander Debate" (partial transcript of debate with Peter Eisenman), in HARVARD GRADUATE SCHOOL OF DESIGN NEWS, editor Yvonne V. Chabrier, May-June, 1983, Vol. II, No. 5, pp. 12-17. Also published in 40 LOTUS INTERNATIONAL, 1983, IV, pp. 60-68; ARCH, March 1984, Vol. 73, pp. 70-73; Japanese translation in ARCHITECTURE AND URBANISM, editor Toshio Nakamura, September 1984, No. 168, pp. 19-28.

7. Jean-Luc Godard, ALPHAVILLE, 1965.

8. Ettore Scola, DIARY OF A POOR YOUNG MAN.

9. Christopher Alexander with Sara Ishikawa, Murray Silverstein, Max Jacobson, Ingrid Fiksdahl-King, and Shlomo Angel, A PATTERN LANGUAGE (New York: Oxford University Press, 1977).

10. The pictures in this section come from André Kertész, J'AIME PARIS (New York: Viking, 1974).

11. Quoted from Christopher Alexander, Howard Davis, Julio Martinez, and Don Corner, THE PRODUCTION OF HOUSES (New York: Oxford University Press, 1985), p. 311.

12. Ann Medlock, "Clergy," in END TIMES TWO (Whidbey Island, Washington: Bareass Press, 1996).

13. For the reader, the plausibility of an interaction between human freedom and the shape of the environment, may be explained further by the nearly 700 pages of examples in Book 3. Although these examples do not explicitly deal with the topic of freedom—but rather with the problem of how a living structure may be generated in human society, and with the shape it takes—still the examples are telling, and gradually build up a conviction that they show what it is like for human beings to be nurtured in the physical world.

14. Director, Makoto Ozawa, NHK, Japan National Broadcasting Company, Tokyo, December 7, 1991.

15. What, in my view, is the full intellectual answer to the puzzle of the impact of living structure on human freedom of spirit is not given until Book 4, chapter 4, where I shall argue that the wholesomeness and integrity of a person's existence is directly dependent on the extent to which that person is able to sustain an inner relatedness with the world in its entirety. I shall argue that this, too, depends on the extent of living structure in that world.

CHAPTER ELEVEN: THE AWAKENING OF SPACE

HOW BUILDINGS WORK

1 / INTRODUCTION

No building (and no part of any building) has real life unless it is deeply and robustly functional.¹ What I mean by this, is that the beauty and force of any building arises always, and in its entirety, from the deep functional nature of the centers that have been created.²

In nature there is essentially nothing that can be identified as a pure ornament without function. Conversely, in nature there is essentially no system that can be identified as functional which is not also beautiful in an ornamental sense. In nature there simply is no division between ornament and function. Traditional buildings, too, often had a unity of ornament and function similar to that which

occurs in nature. But within contemporary ideas about buildings, on the other hand, the division has existed. The more conscious architecture of our own time has largely failed in this respect. We have had function as a mechanistic concept, and ornament as a superficial and stylistic concept. Neither has been satisfactory. Indeed, in our time, the separation of ornament and function has been one of the symptoms of the breakdown of architecture. In this chapter, I shall present a vision of building in which there is a single idea that embraces everything that we have learned to speak of as ornament and function — without dividing them.

2 / ORNAMENT AND FUNCTION

I shall try to show that the functional behavior of buildings, the human life present in them, like its geometry, can all also be understood in terms of wholeness. That means that emotion, movement, light, comfort, climate, balance of functions, the ability of a room to accommodate the behavior in the room, the engineering structure, the manufacturing — all these practical matters can be understood in terms of centers. I shall argue that the full harmony of a functioning building, in the deepest functional sense, is itself something which can best be understood as a product of the wholeness and the field of centers. This means that practical everyday life in and around buildings is more geometric in its nature than we commonly believe, and that all of it can and must be understood as something geometric happening in space.

What, then, is the relationship between order and function? Given the insights of the last chapters, how shall we now understand the idea of a building "working?"

During the early and middle 20th century, the idea of function was for the most part understood in a mechanistic spirit. In trying to work out what a building ought to do, how to analyze its way of working, one had the approach that the building's functions were to be described by a kind of shopping list of "goals." These goals were defined by the architect or engineer, then achieved. It coincided with an idea, due to Bronislaw Malinowski, current in anthropology, that function in anthropology was to be understood also by a kind of shopping list of needs which were met or not met in various ways by the institutions of culture.

However, there were unsolved puzzles inherent in this idea of needs or goals. Those of us who made lists of functions were aware that these lists were inherently arbitrary (dependent on the architect or client who made them, their forgetfulness, lack of insight, etc). Where was the real list of needs? Where was it to be found?

I remember making a long list of some 390 requirements which were to describe the ways in which the rapid transit stations could malfunction. But still, there was an intuitive sense that such a list might be wrong, might be missing items, might be profound or shallow. What these terms meant, or where they might come from, was never answered. The goal analysis of such writers as Churchman, Rittel and others did little to bring insight to this intellectual puzzle. Goals were always arbitrary in some essential way, which could not be mended.

There were further difficulties. The list of needs or goals, no matter how carefully stated, could only with difficulty be connected to the physical form of a building. And the beauty or form itself was even more elusive. When it came to the physical beauty, ornament, gracefulness of appearance, these matters, obviously important, were in a different category.

So one had a split view of architecture, in which two separated and warring categories of content existed, could not easily be fused: function and beauty, ornament and function. Some architects turned toward formalism (were occupied with the geometric aspects of the beauty of a building). Other architects became socially aware, and became occupied with the functional aspects of social process, social need, ecology.

This rift between ornament and function characterized an era in architecture that lasted almost a century. The two were not easily unified. During the 20th century, the possibility of finding ways of designing or thinking about beauty and function in one breath seemed remote and unattainable. It was not possible, intellectually, because we did not have the right intellectual tools. It was not possible, artistically, because we could not think our way into a unitary frame of mind where the two could be fused, unified, in works of beauty which worked profoundly well. That was the state of architecture, almost without change, throughout the 20th century.

But within the view of order which I have put forward in this book it is possible, in principle, to unify these two broken halves. It is possible to think of architecture in a single way where beauty and function—both contributing to life—can be understood as a single unbroken whole.

Function, like wholeness itself, is all based on centers. Function is simply the dynamic aspect of wholeness. A structure, viewed in a static sense, has to do with the system of centers—that appear in it. As something lives, acts in the world, interacts with the world, different centers appear and disappear. Some are moving, some are temporary. The flux of these moving, transitory centers, and their appearing and disappearing, is the process we call life.

The process we call "function" is the process by which the static system is—or is not—in harmony with this moving system of centers that we call life. Water flowing in a stream, nutrients growing in a biosphere, forces in a girder, cars moving on a street, rain falling, people sitting and talking—these are all centers rising and falling in the world. Thus, as cars cross a bridge, they form centers. Each car in itself is a center; the stream of cars forms centers; a traffic blockage is a center. The road system, which has its own geometric centers, is then either harmonious, or not harmonious, with the system of cars that are parked, moving, standing, and so on.

When they are harmonious and co-adapted, we call the system functional.

Essentially, the insight comes from the fact that the goals are not external to the form. We cannot successfully describe a building with goals, because there remains, always, an infinite regress. Instead, we take the idea of life as a primitive notion, and recognize that everything about the life of the building encompasses both form (geometric structure) and function (its behavior).

There is nothing except the living structure of the world, and this living structure is all we need to reason with. We can fully describe all function, through living structure, and the living structure exists recursively, within the idea of living centers.

3 / HOW A CHISEL WORKS

Consider a simple Japanese chisel. It has a handle, shaft, blade, tip, and so on. It works because of its centers. Each kind of working that exists in the chisel inheres in one of the centers which we see in the chisel. The tip of the blade is the cutting edge — this is a center that does the cutting. The handle is the right size and shape for the hand.

The tip of the handle is bound with a steel ring, so that if you hit it with a hammer it doesn't split. The steel binding at the lower end is another center, which stops the wood from splitting. The shaft of the blade, where the blade meets the handle, allows a handle to be put on the piece of steel, and makes a firm connection. This shaft is another center, and it does the work of making a firm connection between handle and blade. The pieces of wood in this part of the handle, alongside the shaft, are centers too — they have the job of making the connection capable of withstanding bending. In a well-made chisel, the geometric centers correspond exactly

to the centers of action (i.e., the way the chisel interacts with the world when we use it) how it cuts the wood, holds in the hand, gets hit by the mallet, and so on.

The functional life of the chisel, the excellence of a good chisel, does not come merely from the fact that these centers exist. It also comes, as in the case of the little stars on the tiled wall in the Alhambra, from the way these centers help each other. For example, the shaft is tapered one way and the wood alongside the shaft is tapered the other way. The shaft makes the wood more of a center: the wood alongside makes the shaft more of a center. The binding strengthens the existence of the blade by being at the other end of the blade. The blade strengthens the existence of the binding as a center.

This idea of helping between centers—especially in this functional sense—may seem mysterious at first. Before trying to understand it in functional terms, I merely draw attention to the following observations. If I take the binding away from the handle end, the tip seems weaker as a center. When the binding on the handle is there, the blade seems to become stronger as a center. Because the handle swells at the hitting end, the steel shaft seems to become stronger as a center.

These are observations about our perception. We shall see later that this phenomenon of one center helping another is not only a perception, but a reality in the world, which is actually responsible for the way the chisel works. The chisel is made of centers, and in a well-made chisel, these centers help one another and mutually intensify their life.

THE AWARENING OF SPACE

4 / HOW A LIVING ROOM WORKS

All life — even in the ordinary sense of practical everyday comfort in a building — is a product of the centers interacting. The idea of wholeness as something which may be sustained or not by its own internal wholenesses goes far beyond the beauty of an ornament. It is the core of the functional life which occurs in things.

To illustrate the idea, let us draw a picture of the way the intensity of centers works functionally in a building. Consider the practical problem of making a comfortable and beautiful living room, which is one of an architect’s most difficult tasks.³ The following issues arise, all involving centers: these centers may be strong centers or not, according to the geometry of the room where they occur. The living room will work well, only when it is so shaped that these centers are really strong, and have life in themselves.

A CORE RESTING PLACE

At the core of a successful living room there must be at least one place which is quiet, a still spot in the room, a place where people are protected, where chairs together have a focus, and are not touched by through traffic. This is the place which everyone naturally goes to when they come into the room. If the room does not have such a place, it will only rarely work: by that I mean that people will have less inclination to be there, to use it, or to be happy using it.

LIVING ROOM AT THE END OF A SEQUENCE

The living room will usually be tranquil if it sits at the end of a sequence of movement. This, too, helps make it quiet, settled. This functional problem will be embodied in the system of centers, which, to solve the problem, must go from the entrance to the house to the living room to form a

GRADIENT of nested centers. Then, like the setting of a jewel, the gradient reaches the living room finally as the jewel encrusted and intensified by the previous centers. It works best of all if the room is the end place, a spot of calm where one comes to rest after moving through the house.

POSITION OF ENTRANCES AND PATHS

Many living rooms are uncomfortable because their key areas are destroyed by a bad pattern of circulation. The movement cuts up the room, and most important, cuts up the possibility of a resting place. To get it right, we have to make the most important center of the room — the still resting place where there is no movement — like the quiet spot in the bend of a river, where the water slows down, and the fish all gather. This means arranging the entrances so that the room — and especially its still, focused, main center — is not interrupted by movement. In short, we want to place those natural paths in such a way that they help the main sitting center of the room, instead of weakening it. They may lead to it, or be tangent to its core, but must not cross it.⁵

THE SPATIAL VOLUME OF THE ROOM

Any room—especially a living room—becomes comfortable in overall feeling only when the shape of the room (its volume) works as a center itself. I do not know of any generally valid rule of proportion—but there is no getting away from the important idea that the proportion must be right for the particular case. In one case, the ceiling may be rather high. In another case, unusually low. In each case, in some different way the comfort of the room comes from the fact that the interior three-dimensional shape, conceived as a volume of solid stuff, is positive. It will usually turn out to be composed of definite spherical shapes. A tall, long, beautiful room might be made of two spheres. Another might be made of many smaller spheres. I remember once seeing a cottage near Shakespeare's birthplace, with a very large room, perhaps 28 feet wide and 18 feet deep—but with a very low ceiling, only one or two inches above 7 feet. It was beautiful because one felt the space as a luminous flat thing; the ceiling was white and softly glowing plaster. In this case, the big, very low room was made of many smaller spheres: but again it was a beautiful shape in the volume (GOOD SHAPE). So, even the elusive question of the space in the room turns out to be defined by the way that the volume is composed of centers.⁶

A WINDOW PLACE

Living rooms are often made, or broken, by the beauty of the windows. To be beautiful, the windows themselves must be "places." This means not only that any important window forms a center in two dimensions within the wall (through shape, position, glazing subdivision, and so on), but also that it works in three dimensions: the actual space next to the window must, volumetrically, itself be a center; it must be a definite place. This is the kind of window which

draws you to it, and which allows you to make yourself comfortable when you choose to orient yourself to the light.

And the window must not only accomplish all this by its own beauty and by its view, but it must also do all this in a way that contributes to the life of the major sitting area of the room. To do that the window as a center itself (size, opening, sill, view) must cooperate to intensify some other center in the room.7

THE FIREPLACE

People feel a need for a smaller focus of some sort in the living room. In the Western world this smaller focus is often a fireplace. In Japan, it might be an altar or a tokonoma.8 A TV set has the potential for it, but rarely works this way in contemporary rooms, because the "precious" feeling is not present. The focus provides something to gather round, something to orient oneself to

ward. Placing it may be hard because people also like to orient themselves toward the main window where the daylight comes in. Then the room must be constructed in such a way that the one center created by the fire and the other center created by the major daylight together help to intensify the main center of the room and do not clash with one another.9

THE VIEW AS PART OF THE INSIDE

Most nice rooms have a good relation to a definite and beautiful outdoors. This requires that some outdoor area works as a center (a flowering bush, a view of a distant lake or mountain peak, the light coming through the leaves of a birch tree). Then the interior center in the room, which is likely to be an important place in the room, must be placed to have an easy and natural axis toward a vital outdoor center (near or far) as a focus, thus forming a new center (the axis joining the two) which carries weight.¹⁰

LIGHTS AS NATURAL CENTERS

We want to place lights in the room in such a way that they create a pleasant atmosphere in the room, not too dim, not too bright, something which maintains the life of the room at night. When you think about this, it means that we want to place lights in such a way that the spheres of light formed around the fixtures induce centers which support the system of centers which makes life in the room. (My experience is that you can best do this with real mockups made with lights, at night, while the room is being built.) If a fixture is correctly placed, but garish in shape or color, it will draw attention to itself as a center, instead of helping to intensify the other centers in the room. The best lights are those which reinforce the structure of the room, without creating other new and irrelevant centers in themselves.¹¹

5 / HOW CENTERS WORK TOGETHER

The centers described in the last few pages are some of the most important structures in a living room. Of course, these centers are important individually. But what is more important is the way these centers interlock and depend on one another for their success.

The quiet core of the room is a tranquil center; its tranquility depends on the paths going tangent to it — other important centers. The window place works when it forms a focus, because then it can intensify, not destroy, other, still larger centers of the room. The volume swelling toward the ceiling, when it is supplemented by the lights, can form a composite center that supports and forms a matrix for the whole. And so on.

In a successful room, these many centers are not merely aggregated. Rather, they fit smoothly together in a single form, so that one is barely conscious of the individual centers, but rather conscious only of the smoothly flowing whole which forms the largest center of all: the room itself. To see this, concretely, it may be helpful to see how these several centers were incorporated in a new living room. Here is a sketch-plan of a living room I built at Meadow Lodge in England. It incorporates the centers I have defined in a strong form, yet in a rather simple, modest, room.

The core resting place is formed as a dead end, in front of the fire. The window has a tree outside, and connects the inside of the room to the tree. The single door is placed in one corner to minimize circulation through the room. The piano makes positive space in the room, and fits together with the "resting place" center and the "window place" center. The easy chairs just fit, perhaps asymmetrically, but in such a way as to make space positive throughout the room. The lights are placed to complement and ring the

other centers, especially reinforcing the resting place at the core of the room. All the centers supplement and support each other.

These functional matters are simple, even obvious. Nevertheless they are surprisingly difficult to accomplish in a newly built room. They are easy to think about, but not easy to embed in a realistic physical structure which actually creates all these forms of comfort at the same time in one room. The structure that has to be created is modest, subtle, and tough.

What is most important here: all the functions of the room — things which appear at first sight as functional problems — are in reality problems of centers. To provide for life, and to solve the possible problems you have to get the centers right. In short, to make the room work, you must make a dense, living structure. The practical matter is a matter of placing and arranging all these centers so that they work harmoniously together. The hard part, the key part, lies in the way these centers are shaped, and strengthened, and arranged.

6 / THE UNITY OF ORNAMENT AND FUNCTION

In the living-room examples, we see that key functions depend on various component centers and on the ways these centers cooperate to intensify each other. The functional behavior of each living room is almost geometrical in nature. What makes the room work is the geometrical intensity, vibrancy, of its living centers, their degree of life. The fifteen properties, the field of centers, and the wholeness not only control the way that beautiful buildings look. They thoroughly and completely determine the way that buildings work.

Altogether I believe the functional life of buildings is created by the same field effect among centers which creates the field of centers in an ornament. Each functional "problem" is solved by the cooperation or integration of centers which arise within the building dynamically, while it is working. The field of centers supports not only everything we commonly call ornament in a building but also everything we commonly call function.

Within a Cartesian analysis, the things that are considered real are those things which can be understood as mechanisms. This means that the functions which can be understood as "real" are only the "mechanically functional" aspects of a building like structural efficiency, thermal behavior, or acoustics.

In the holistic picture which I have been describing here, we see that each center—as a bit of geometry in the space—affects and changes the other centers in its life. The wholeness is a physical system in which different centers modify each other through the geometric field effect. In this picture, centers may affect each other both geometrically and functionally, since all the effects among centers take place within the same domain. Ornament is just as important as function. Indeed, we cannot separate the two from one another. What we call ornament and what we call function are simply two versions of one more general phenomenon.[12]

SOCIAL COHESION IN THE FRENCH VILLAGE OF “G”

For the sake of further illustration, let us consider a study by Bill Hillier and Julienne Hanson, who explored, with extraordinary thoroughness, the question of communication in a human community, and the way this is supported by social and spatial structure as they act together.[13]

Their study included field observations in communities throughout Europe, together with data collected widely from the anthropological literature. In the course of a 270-page book of careful empirical field-work and many computer simulations, they seek to correlate the ground plan of a village or neighborhood with the level and nature of human communication that takes place in that community. Above all, Hillier and Hanson looked for key structural variables which play a controlling role in the quality of this human communication.

One of the key functional issues they have identified, is that the human communication will be good, or not, according to the degree that the village or neighborhood contains instances of a structure they call a beady-ring structure. A beady-ring structure, illustrated in the drawings

of the traditional French village “G,” which they cite extensively in their study, is a closed loop of small convex positive spaces, connected by paths. The plan of G, its public space, the positive or convex spaces which the village contains along this path structure, and the resulting beady-ring structure are shown in the accompanying drawings.

One of their strong conclusions is that the quality of human communication in a village or neighborhood is largely dependent on the presence, and density, of these global beady-ring structures.

I bring this example forward in some detail, because what turns out, after the careful, and beautiful, and lengthy analysis, is that the characteristic which most makes the community work, in human terms, is the presence of a particular type of center—the thing they call the beady-ring structure—and the density of these beady-ring structures in the community; also people's access to such structures, from their houses and shops. It is also worth noting that they explicitly show how the beady-ring structure is a global configuration composed of local centers—it is a ring, formed from small positive spaces, connected along a path that forms the loop.

These beady rings are living centers (not always present in a neighborhood) which, when present, enhance the centers formed by houses and gardens and streets. It is the presence of these supporting centers, and the resultant increased density of living structure, that makes the community work.¹⁴

It is highly significant, in my eyes, that throughout their careful analysis, Hillier and Hanson reach conclusions similar to those I am presenting in this chapter about the unity of space and function. As they say: “Society must be described in terms of its intrinsic spatiality. Space must be described in terms of its intrinsic sociality.”¹⁵ In my language, they are saying—as I am also saying—that it is not really possible to keep function and space separate. Rather, what is needed is an integrated view of function and structure, in which the living character of space is visible as a characteristic of the integrated whole.

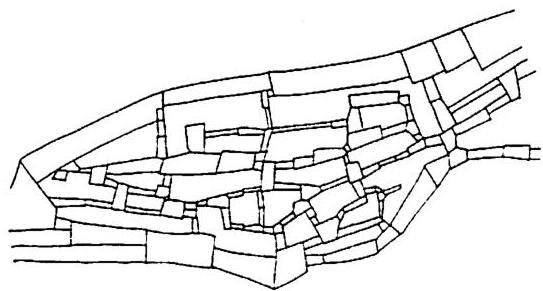
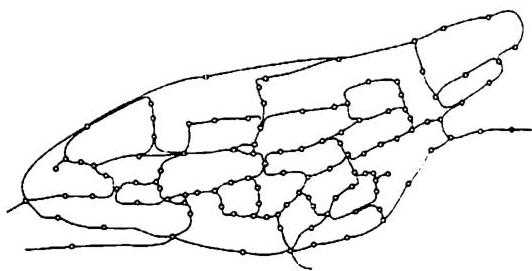
STRUCTURAL BEHAVIOR IN TWO COLUMN-BASES

Consider the following “functional” problem involved in designing a column base. In today’s architecture and engineering it is common to design on the basis of purely structural considerations. Let us assume, for the sake of argument, that such a structural analysis of a column base shows that what is needed is a pinconnection: one which can take tension and compression and horizontal shear—but no bending moments. This is one common design approach to a conventionally analyzed column base.

Following this approach, and looking at the design of the column base in limited functional terms, we can get a design for a base which consists of a triangular piece of steel at the bottom of the column, meeting another triangular piece of steel that is welded to the base, and the two are connected by a bolt. The bolt itself and the distance from the bolt-hole to the edge of the steel are designed to be the minimum required for the necessary shears and compression. The base then looks like A (the upper picture).

Intuitively, this is a pretty funny-looking column base. It certainly doesn't resemble the kind of base which I would show you as a good example of life in a column. A column with life

would typically look more like B (the lower picture).

Where does the discrepancy between these two views, or between the two designs A and B, actually come from. I believe it comes from the narrow limitations introduced by conventional functionalist design. If we are more truthful about column behavior a column base can be said to have many functions, including at least the following eight:

1. It is larger than the column so it becomes something to lean against.
2. It has a function in defining positive space next to it.
3. It may be a place to sit.
4. Structurally it spreads the vertical load onto the foundation.
5. The base may also have to provide horizontal resistance, to stop the column from moving out of position.
6. From a structural point of view, there may also be redundancy which comes into play if the pin connection fails in an earthquake.
7. In addition, moment design at the base may play a role.
8. The base may also play an important role in the erection of the column, by marking the spot where the column is to be and providing an attachment for this column.

These eight functions are all relevant to the design of a column base. The important question is not, Which of them should we choose? but, How are all eight different functions to be balanced?

The pure functionalist analysis which argues for the highly efficient pin-jointed base comes about, really, because one particular function that we can identify (#5) is made very important, while others are ignored. The pin-jointed base mainly deals with function #5 and gives it great importance. It more or less ignores the other seven functions. If we take the view that the balance among them is arbitrary, and a matter of choice for the designer, the pin-jointed base can then be a reasonable, and perfectly plausible solution — along with fifty other possible

bases, which might all be calculated to meet different combinations, or different weightings of these eight functions. The pin-jointed base gives 100 percent weight to the restraint of horizontal forces, zero percent weight to leaning against the column, forming a place next to the column, and zero percent to all the others too.

However, if we look at the base as a center whose life we are trying to intensify—and we accept the idea that this "life" can be understood, measured, by direct observation—then we get something much more like the second picture, where the eight functions are more in balance. On this page I show some cast-concrete porch columns which arose from a modern effort to

balance all eight functions more equally. But what it also does, is to pay more attention to the centers: The base, the shaft, the flutes, the space between the bases, and so on.

We see here how asking for the life of that center which forms the bottom of the column helps us to balance all the functional issues. And, more important, it argues against the one-sided choice of any one or two functions.

What is involved in this approach is that we pay attention not only to the functions themselves, but also (and rather) to the overall life of the system as a whole. The approach treats the space as a whole, and tries to make it more harmonious, more alive, more unified as a whole.[16]

THE LIFE OF A SHAKER ROOM

The issue of functionalism comes clearly into focus in the works of the 19th-century Shakers. Many people would say that the Shakers are famous for their practical ingenuity, and that what they did arose out of utter, pure practical considerations. In their work we may therefore see the issue of functionalism at its clearest.

Here is one example of their work in action: they made pegs, put the pegs on the wall, and hung chairs on these pegs. This is amazing practicality, taken to a spiritual extreme. They wanted to keep the floor clear for their celebrations, as well as clean and uncluttered, so they had the amazing (or inspired) idea of hanging ladder-back chairs on pegs around the wall, which were already being used to hang clothing, baskets, and other things. The form followed directly from the function. What seems remarkable and beautiful is that the function was taken to such an extreme.

But I believe that this analysis is wrong. Consider for a moment the configuration of such a Shaker room. It has a clear, uncluttered floor,

and around the walls of the room is a pine board at about head height. Along the board, regularly spaced, are beautifully shaped pegs. And hanging from these pegs are ladder-back chairs.

Think of this as a system of centers. The room as a whole is extraordinarily beautiful and pure. The clear space below the chairs is THE VOID. The ring of the board with its pegs and hanging chairs is like a crown, forming the space, surrounding it, embellishing and creating and intensifying that void. It is a deeply spiritual form. To summarize it, we may think of the space as a crown, a void center, ringed about with centers, each leading to smaller centers, just as in a medieval crown.

In my view, the compelling and driving force behind the Shakers' idea of the hanging chairs was the creation of this "crown." I believe that a purely mechanistic view—the Shakers did it to clear the floor or to find a use for their marvelous and highly practical pegs—is a misunderstanding, caused only because our understanding of what it means to be "practical" is so limited, so narrow, and so mechanistic.

I suggest that being practical, for the Shakers, included finding a system of centers which had a pure spiritual light revealed in it. It is the invention, creation and propagation of the crown structure of centers which meant everything because it was this which instilled in them, and allowed them to preserve, a spiritual state. And we do feel this in the rooms they made. If the Shaker room was a machine at all, it was a machine for inducing and intensifying this spiritual state in a person who is in the room.

Our difficulty, though, is twofold. First, we fail to understand the way in which this system of centers, when properly created, does induce a spiritual state in anyone who comes in contact with it. Second, we cannot easily find our way to a conception in which we understand that the creation of this crown—this system of centers—is not formal, but both formal and practical. Of course, clearing the floor is part of it,

too; of course, using the ingenious pegs on the wall is part of it. But we do not easily understand a mentality which is both practical and spiritual at the same time. For us, it has to be either/or. It is either formal/geometrical—and then not practical and functional—or it is practical and functional but not geometric or spiritual. This conceptually limited view interferes with our efforts to understand the full, complex nature of life, and inhibits our attempts to create it.

The life which I am describing in this book can be created only when we understand that such a structure is both geometrical and functional and that it cannot be one without the

other. It is not the two things added together. The conception of living centers which forms the crown is a conception which includes the fact that the floor is clear and dust-free, includes the spiritual state coming from this perfect emptiness, includes joy in the fact that the pegboard is a being-like structure made of centers which has life because of its internal geometry, and which is also practical and easy to make because of its geometry.

That wedding of geometry and function deep down in every center—that is the origin of true function, and the wedding we must make in our minds.

A SHAKER BOX

For a smaller version of this kind of thinking, let's look at the finger joints on a small Shaker box. It starts as a formal beauty: it uses GRADIENTS, DEEP INTERLOCK, and ALTERNATING REPETITION to get a beautiful organization. It is almost a pure ornament. But it happens to be deeply practical. Suppose, for instance, we merely lapped the one layer over the other, and

set small brads into it. The part between the nails would be hard to glue down: the open edge would tend to wrinkle or spall up. So we place the nails, and then bring the shape of the lap close to the nail pattern, so the glue is always near a nail.

Did this start as a practical idea, which then just happened to be beautiful? I do not think so.

After thinking about it carefully, I am certain that it started as a formal intuition about the field of centers, even if the maker did not think in this language, and that it then gradually fitted itself to the functional problem at hand. Again, it started with an instinct for what is beautiful. I believe the maker therefore concentrated, while working, on the wholeness, what I call the field of centers. When he came to the lapped joint I suspect he explored mainly those possible versions in which the field of centers is strong. This inspired him, and led him to the beautiful and practical solution which we see in the example.

First, he realized while bringing the thin piece of wood around, that it would be a beautiful way to connect the two leaves to let one lap the other in a kind of interlocking pattern. The ALTERNATING REPETITION of the brads and spaces, the GOOD SHAPE of the curve which makes the lap, etc., all make the box beautiful and unified.

Then as a by-product of this primary intuition he found that each of these instincts about the formal beauty corresponded to a practical problem that had to be solved. Each way that the

smaller centers help to intensify the larger centers — and make a field — corresponds to a practical need which exists in the real materials of the real box, and which must be satisfied practically

in order for the centers in the real box to come to life.

Thus the good shape, which gives each piece that curve, makes the centers bulge at the left-hand end and thinly taper at the right-hand end, and so strengthens the other interlocking centers in the lower piece of wood as much as possible.

This has a practical advantage which follows directly from the structure of the centers. The center is fat where the brad is going to go, where it needs to be fat, and narrow where the glue is going to go, where it wants something thin which cannot curl and warp. Each of the ways the centers work together, in the formal sense, has a direct practical effect in the real thing.

It seems hard to understand the idea that people were able to invent something practical by starting with the phenomenon of the field of centers. It goes against the grain of our contemporary moral intuition. However, objectively, it is not hard to understand. The field of centers deals with the idea that centers have to be supported by other centers. If we start with a geometrical attitude in which we try to make a field of centers everywhere, this then establishes a kind of seed-bed for practical functions because the field tends to create a structure in which the various centers are able to help each other functionally.

If, on the other hand, we fix the shape of something by trying only to be practical, not thinking about the field of centers, it is possible to get good results—but it is less likely. The field, I suggest, is the most fruitful structure that exists for function. If we ignore the field it does not mean that we cannot find our way towards it by purely practical and functional arguments—but it is less likely to happen.

7 / FUNCTION ARISING OUT OF ORNAMENT

In hundreds of examples of deep function, as it occurs in buildings, I have found again and again—without counter example—that our ability to see the field of centers in a thing, and to produce the centers which are indicated geometrically, tends to produce an object which works better. This, I believe, was the experience of the craftsmen who made the things I have described. And I shall try to show that this is true in general.

Because of our still-prevailing 20th-century viewpoint, students are convinced that "beauty" comes about as a result of the concern with practical efficiency. In other words, if you make it practical and efficient, then it will follow that it becomes beautiful. Form follows function! But if we look at the examples I have given, it seems very unlikely that this is what took place when they were made. They were made deeply practical, yes. But they became deeply practical because their makers tried to make the centers strong. Example after examples suggests emphatically that this is what came first: making the centers beautiful was the driving force. The practical efficiency that came along with it was a vital part of the package. But it was never the driving force in the mechanistic sense that we believe in today.

Yet, today, this is so difficult to accept. In discussing these examples with students, I have often had a hard time convincing them that good and functional structures achieve their quality from a conscious effort by the maker to make the geometric field of centers. The essence of this point—because it puts its emphasis on beauty, not on puritanism—has seemed immoral, even heretical, to many of my students. They—often the most rational and most intelligent students—have an almost moralistic passion in their desire to prove that these beautiful things must have been produced by purely functional thinking. When I point out that these structures have a highly for-

mal, geometric field of centers in them, they shy away from this thought—possibly because it sounds to them as though I am claiming something flippant or immoral, while they are thinking that since these things are practical and efficient they must have been created from the point of view of functional and practical efficiency.

It is a natural mistake to make. Within the mechanistic world-view of our time, it is natural to assume that something efficient must have been shaped by the desire for efficiency. But even when I point out that modern attempts to make things practical and efficient cannot be relied upon to create this formal beauty, and therefore cannot explain it, the students still have a hard time grasping this circumstance.

Yet we may see this once again in the case of the nails. The geometry that occurs in the 14th-century nail produces life that has both functional and ornamental qualities to an extraordinary extent. By contrast, later examples—a 19th-century nail for instance—has less life, and the modern nail has almost no life or physical geometrical beauty at all.

In medieval times, even something as ordinary as a nail was viewed like this. In the 14th-century nail shown below, we have a thing which has intense life. It is beautiful and has life as an object and as an ornament. It also works incredibly well. Because of its size, and the thickness of the head, it has a very long life and great strength, lasting in some cases 600 years—something that a 20th-century nail could almost never do.

Is it a coincidence that the 14th-century nail works so well both as an ornament, and as a functioning long-lived nail? What is the connection between the ornament and function in the nail? It is not coincidence. Somehow the way the centers work, in the "ornament," the heaviness of the head, the "being-like" nature of the form—somehow this is reflected, or duplicated, in the functional life of the nail, in its long-wearing capacity, its strength, its durability, the fact that the nail head will never shear or tear as a modern nail head will do.

In the French village studied by Hillier and Hanson, there was a cohesion which was intense. It was not merely some kind of functional life, due only to social cohesion. It was not merely some kind of geometric beauty due only to the physical coherence in the geometry. It was undifferentiated, primal, a kind of life that is inherent in space and society together.

In the 14th-century nail, too, we have a life which is intense. Again, it is not only functional life. Again, it is not only ornamental life. It is simply life, a quality which appears to be an attribute of space itself.

8 / LIFE AS AN ATTRIBUTE OF SPACE AND MATTER

The architecture which follows in Books 2 and 3 is based on a conception of the world in which the air we breathe, the stones and concrete our city streets are made of—all have life in them, or not; all have life, anyway, in varying degrees.

Our job, as architects, builders, citizens, is to create this life in the air and stones and rooms and gardens—to create life in the fabric of space itself. This is not a merely a poetic way of talking. It is a new physical conception of how the world is made and how it must be understood, which—if it were accepted—would change, utterly, our conception of the world.

It is admittedly extremely difficult to visualize the idea that space and matter, the matter/space itself, could, as an attribute, have life in varying degrees. Although I have managed to show earlier that the recursive scheme in which life spawns life, life comes from life, still, the idea of life as an undefined primitive feature of matter/space, without further meaning that can

be expressed, is very, very difficult to swallow or to understand. If it were not for the fact that so many practical matters about architecture become comprehensible within this frame of reference, I think one would not even have a reason to attempt it.

And indeed, I shall not be able to attempt a thorough explanation of this idea until Book 4, THE LUMINOUS GROUND. For the time being, though, one needs something to grasp at, some idea which allows one at least a hint of what it might mean. In the remaining sections of this chapter I shall attempt it by suggesting, informally, that the appearance of life in space may be compared with some kind of awakening, almost as if—as it comes to life—space itself, the very matter, wakes up, awakens, and that it is this awakening of space in varying degrees—indeed in infinitely varying degrees—that we recognize when we see life in space, when we see life in buildings, in the mountainside, in a work of art, in the smile upon a person's face.

9 / THE HYPOTHESIS OF DENIS DIDEROT

So, what we have is that the analysis of all function should be done in terms of our effort to make every center precious. That means the basic rule of function is simply this: we try to make every part of the world precious, as far as we can. It sounds childish. But it is not.

In our normal Cartesian mode of thought, we try to explain the life we notice in the centers in the world around us as a mechanical result of other conditions. For instance, I tell you that the life of the window seat I showed earlier comes about because of small panes, because of the light coming from two sides, because of the pale color of the wood, because of the cushion on the seat.[17] These observations are all true. But if I take another window with these characteristics, I may

get life but it is certainly not true that I will get it to a predictable extent.

Certainly these things, the patterns, the properties, may play a role in my being able to create life in things. They actually do play a role. But they are far from certain. What is more certain is my "interior" sense of the life. Thus the life is really the primary thing, and the properties are really secondary. Because of the Cartesian scheme, I assume that the life is a construct, and that these primary characteristics are more basic. But this is just an intellectual assumption. And, I believe, under careful scrutiny this assumption shows itself to be untrue.

It is far more accurate, and more simple, to say directly that this window place has life, that

I can see that, and that the degree of this life can be directly observed by me.

Someone may say, Well, the degree of life is noticed by you, but how objective is it? Again, objectivity or the lack of it is not, I believe, the reason why people are reluctant to speak about such things in easy terms. It is more true that there is an intellectual prohibition against saying that the window place has life, than that there is really a factual dispute about the degree of life it has. As I have mentioned earlier, when paired comparisons are shown to people the people tend to agree about which example has more life. The idea that the window place has life is directly congruent with our experience.

Thus I must stress that the idea that every part of space has life in some degree does not violate our actual experience. If we look around in the world, at the different parts of space, it is relatively easy to say, "This one has more life, that one has less life." What is violated is only the picture of space which has been put in our minds by Descartes and by the assumptions of mechanistic science. Descartes specifically described space as a neutral and strictly abstract geometric medium.[18] Almost all of modern physics, with its basis in the algebra and arithmetic of Cartesian geometry, has followed Descartes in this idea. But it is an idea, not an observed fact. It is not empirical. The Cartesian dogma and its assumptions are

methodological teachings, useful models. As presently formulated, they are violated by the idea that every part of space has some life. But experience itself is not violated by it.

The necessity of seeing matter as potentially having life was taken up 250 years ago, quite directly, by Denis Diderot, one of the great figures of the Enlightenment. In the following passage from D'ALEMBERT'S DREAM, he refers to the idea that space has life as "a simple hypothesis." He writes: "You will come to feel that by refusing to entertain a simple hypothesis that explains everything—sensitivity as a property common to all matter or as a result of the organization of matter—you are flying in the face of common sense and plunging into a chasm of mysteries, contradictions and absurdities."[19] In other words, in Diderot's view, the hypothesis that matter and space have different degrees of life is easier, less complex, and more straightforward than the hypothesis that matter/space is a neutral machine which, as a machine, has to be able to produce the almost magical qualities we see!

We will understand reality itself better if we can educate ourselves to abandon the mechanistic picture, which doesn't work, and concentrate on the picture of the living centers—which, no matter how strange to our present-day mentality—actually does work.

10 / SPACE ITSELF CARRIES THE ATTRIBUTE OF LIFE

The examples I have given show cases where a building has an opportunity to intensify the life which exists in space. The creation of a window which is a "window place" intensifies the centers in the living room, makes them more precious, and increases the life which exists in space.

The normal way of understanding this example is to say that some system of needs or forces or processes exists—and must then be resolved by the structure which is designed. But

in fact this idea doesn't really make sense in the examples. We never really get a chance to understand what it means to say that the needs or forces are resolved. This whole "functionalist" way of talking about space is an elaborate circumlocution whose purpose is to make us feel that we understand—without creating real understanding in our minds.

On the other hand, the view that space and matter can have life — more of it, or less

of it—as in the illustrated cases where the living room space takes on more life because of the organization inherent in the created field of centers, really does contribute to our concrete understanding—provided we can swallow the idea that space itself really can have life in different degrees.

I have said that centers help one another come to life, and that this “helping” is both functional and geometrical. But if the visual helping between the centers and the functional helping between centers are connected, how are they connected? A first answer is that something is occurring in a deeper domain than either function or geometry. The question then is, What domain? The answer might be given as: the domain where all this is happening is some domain of emergent life, a domain of space somehow “waking up.”

Hence when one region of space wakes up and then wakes up another region of space, there is also a functional connection which gets established. This mysterious structure, presented hitherto as centers happening in space, is actually a sequence of awakening in the more fundamental domain.

In this sense, what is going on is that life — an emergent thing in the space itself— appears as the space wakes up. When something works, or is “functional,” its space is awakened to a very high degree. It becomes alive. The space itself becomes alive.

Just to be completely sure of this point, let us review once more a case of something which may seem to us like pure function: daylight in a room. We know that daylight gets better when the light comes from more than one side. This has been discussed at length in A PATTERN LANGUAGE.²⁰ Further, if we examine carefully the real nature of the light in a room which makes us feel comfortable, we see that it is broken into a myriad of dappled patches of light, gradients of light varying on the plaster or the wall. The light which comes in, even from the trees and sky outside, is already dappled and then breaks into a thousand further dappled shining bits as

it bounces around the room. This is a room which makes us feel comfortable.

On the other hand, a room which has flat, artificial light, which makes us feel uncomfortable, is a room in which this natural bouncing and breaking of the light is prevented, a room in which the light is artificially smoothed out and homogeneous, where there is no “play” of light.

The room where the light falls is a center. The fact that this center is intensified by the patches of light simply indicates that this center is supported in its life by the life of these smaller centers of light. If I try to understand what to do with the light, and give an analysis in terms of lumens per square foot, or the need for efficient energy use, I get nothing clear—because I can multiply these kinds of reasons ad infinitum—and will never know how to put them in balance, nor which ones to consider most important.

The issue becomes clear when I stop asking these mechanical questions about the light (which I can never evaluate anyway), and instead take a balanced picture of the whole, in which my sole interest is to intensify the life of the room as a center. To do this, I need to find ways in which the life of the room, as a center, depends on the life of smaller centers—and I then need to elaborate these smaller centers in a way which makes this increase of life clear and definite.

You may ask how we can be sure that the light needs this sort of thing, or how we can be sure what indeed is greater life, whether in the patches of light themselves or in the room. The answer is simple but strange. I do not know why it should be true that the greater life of the room depends on the greater life of the individual patches of light—but I do know that it simply is so.

The fundamental functional insight is to realize that the mechanistic functional analysis is all a myth anyway—since there is no stopping in the endless regression of reasons for why something works. What actually fits our common sense, and what we really do when we think about such things, is always, and only, to create this greater life out of greater life—and to make

that answerable only to itself. There is no other reason behind it.

This is the surprising discovery about function, which makes us see function itself in a new way. If a thing gets its nature from its field of centers, and if the primary interaction between centers is the one in which they help to prop each other up by consolidating their centeredness, then what we commonly call ornament is not different, in principle, from function. If we understand the idea of the field of centers well, we shall have a picture of the universe as made of stuff — space/matter — which is potentially living stuff. It is a material in which the occurrence of centers produces more and more intensity of centers. The material actually transforms, comes to life, becomes transformed, "blazes" one might even say, as this field of centers is created in it.

Within this understanding, the distinction between function and ornament is spurious. Every emerging or unfolding field of centers is a

part of the universe which becomes vigorously alive — privately, I like to think of this as a more blissful state of matter. As the whole emerges, the universe becomes ornamented by it. The rules of the emerging thing are exactly those which we have noticed for so-called "pure" ornament.

In this understanding a flower, or a river, or a person, or a building all have the same potential role. Each of them may be judged by the extent to which this pure blissful structure comes into being, and by the extent to which the light of the universe shines through as a result of this creation.

So we come back finally to the recognition that even what we think of as "life" or "function" is something which must ultimately be understood as pure structure, something lying purely in the space, as an attribute of the space itself. It is the matter/space itself which comes to life. And, when it does so, there is no difference, in principle, between what we have historically called "function" and what we have historically called "ornament."

11 / THROW OUT ALL FUNCTIONAL EXPLANATIONS IN YOUR MIND EXCEPT THE LIFE OF CENTERS

I am suggesting that we can best assess function by assessing the degree of life in various centers; and we can get the clearest picture of what to do when faced with practical design choices by focusing on the life of individual centers. Intellectually, this technique leads to a remarkable change in our understanding of the world.

In the mechanistic positivistic way of thinking, we assume that we identify certain needs or functions—and the design must then "meet" those functions. The geometry and function come, intellectually, from quite different worlds. In our minds, when we are thinking like this, the two things—function and geometry—are logically different in type.

But if the secret of balance lies in the life of the centers themselves, this leads to a conception

in which space and function, function and geometry, are truly unseparated. We do not have function on the one hand, and space or geometry on the other hand. We have a single thing — living space — which has its life to varying degrees. It is the space which comes to life. All that we do, as architects, is then to arrange and rearrange this living space, in such a way as to intensify its life.[21]

The medieval blacksmith does this with his iron as he forges it, and makes the living nail. The architect or engineer does it and makes the living column base. The builder does it with materials — plaster perhaps — and makes a plaster surface come to life. The biologist does it with a living ecosystem, and makes a pond or a forest come to life. The regional planner does it with

the distribution of human settlements, agriculture and transportation, and again makes living space as intense as possible. The painter does it with color, the carver does it with indentations, the tileworker does it with glazes and patterns. No one of these activities is any more ornamental than the others, or more functional. What is created in every instance, even the biological, is living space. It is all living space.

To come to grips with the idea that space/matter itself might really be alive, let me describe a natural and much larger system: the organic system which I may call a meadow. Consider a meadow, a place in the hilly brushland of Northern California, where grasses, trees, shrubs, growing wild, have been cut back, pruned, in such a way as to create living space. This meadow is first of all, fire-safe. In an area prone to catastrophic wildfire, the spread of fire is slowed down, by a kind of planting arrangement in which many small meadows, with open grassland in the middle, some bushes and trees around the edge. Such a place is resistant to the

spread of fire. The sunshine in the meadow invites use. The trees around the edge, provide a picnicking family with a place to lean against. The lower shrubs, forming barriers, and space enclosures, create a place for butterflies, and wild birds. Meadow wildflowers flourish in the open meadow. A lone oak, here and there, creates a majestic center, its trunks pruned bare, to reveal the canopy, and the spread of beautiful space which the oak creates for animals and human beings. Eucalyptus, invaders from Australia, are kept back, the acid leaves not able to contaminate the soil; Broom, transplant from Scotland or France, sparkles in the sunlight, but is also kept low and managed. The grasses, native grasses, create a turf full of seeds, rhimes, of wildflowers, and perpetuates the naturally occurring biological species.

The meadow has STRONG CENTERS formed by the meadow itself and its BOUNDARIES. The rills of bushes and low grass alternate, providing cover for small animals and deer, and geometrically forming ALTERNATING REPETITION. Trees

in their majesty form LOCAL SYMMETRIES. The slight declivity which provides a view over the San Francisco Bay, forms a subsidiary STRONG CENTER and subsidiary LOCAL SYMMETRIES. Paths, formed by the deer and people, provide other LOCAL SYMMETRIES, and ECHOES in the landscape. The meadow forms a VOID; each thing is barely distinguished from the neighboring structures, thus making NOT-SEPARATENESS from all of it. There are GRADIENTS of shade, gradients of moisture, gradients of plant type, gradients of height: these gradients assure combinations for a huge variety of plants and insects, thus making the place biologically richer.

There are ECHOES in each meadow, of the larger structure of the land and of the hills.

This place has life, certainly. But exactly what is it that is alive? Much of what we take to be alive, stones, paths, an old fence, concrete fence post, the earth and soil, are, strictly speaking non-organic, although they harbor smaller animals and molds. The life of the whole may be described as a web of interconnecting dependencies, among the various species which thrive in one another's company. But what is it that is alive?

It is alive, because the many, many, many centers help each other, in their mutual life. It is alive because of its structure, and because of its geometry. What is alive, is the earth, and rock, and space itself. The life includes the air, again inorganic. Yet, without doubt, the whole thing is alive.

I describe this—I only know how to describe it—by saying, frankly, that the whole system, the space itself with its material, has come alive. It is not life in space, not an inorganic mechanical substrate, filled with a few living organisms. It is one living thing, the space has come to life, it is nonsense to separate the two.

And if you too feel something like this, then with Diderot, you may frankly say this idea is simpler, and more direct, than saying that there is a dead mechanical world, in which a few living creatures have appeared . . . far simpler to say that it is all alive in its cooperation, and that

space itself, the space we formerly thought of as a dull, mathematical, cold, inorganic medium which houses a few living things, is itself—rather—touched, sparked, and burning.

To come to grips with the idea that space/ matter itself might really be alive, let us try the same thing, once again, but now with a much smaller system. Let me describe an isolated Japanese ridge tile I have in my house. It is a lovely traditional ridge tile which is to be placed at the gable end of the peak of the roof.[22]

By looking at this tile, let us try to come to grips, more vividly than before, with the meaning of this pure life, or pure "centeredness" which can happen in a thing. Look carefully at the tile. You notice, of course, that the tile works as a living center. But probably you do not fully realize, at first, that this quality of being a living center comes from the interdependence of other living centers which it contains. At first we see only that the center we see as the tile is literally "in the middle." It is the big upside-down U-shaped space in the middle of the whole thing.

Now when we study it, and try to understand why this upside-down U works as a center, we notice that the centeredness comes from the existence, around this upside-down U, of other centers: the boundary, the ridges which contain the boundary, and the nearly spherical balls or circles which appear along this boundary.

So, like so many other examples I have used, the tile gets its centeredness from the cooperation of many smaller centers which it contains. The small balls or circles around it form powerful but minor centers. It is the way they ring the main upside-down U-shape which gives the U its strength. The boundary line is itself a center, and its strength or life as a center also contributes to the force and power of the center which the whole tile creates. And, of course, the subtle and beautiful shape of the tile as a whole also adds to the feeling of life in the center which is created there.

What is it then? What is the center that has been created? We keep coming back to that question. What has happened in space as a result of this geometric disturbance that we call its

shape or its design? What is the center, in space, which this piece of clay creates?

To grope for an answer to this question, I want to make an observation about the centers: each of the centers in the tile gets its own feeling, its own depth, from the fact that it is helping the larger center come to life. This is an important idea. The balls around the edge have a special living quality. They aren't just "circles." If you look at them carefully, try to understand their life, and examine your own feeling about their

life carefully by introspection, you will notice that it comes about because each of them, and all of them together, are helping to create the life of the tile as a whole. It is their presence in the whole, and the fact that they are helping the life of the whole, which gives them their individual life as individual centers. And in the process, they become precious.

You may grasp the same idea — more vividly perhaps — if you think about a person's foot. The foot is a center. It gets its life as a center as it is helping the whole organism. Its life as a center comes from the fact that it is helping to create the larger life of the person as a center. That is what makes the foot profound. The foot literally cut off, viewed in isolation, or literally hacked off a living person's leg, does not have that special quality, because it is no longer helping to promote and maintain the life of the larger whole.

These two things are true of every living center:

1. Each center gets its life, always, from the fact that it is helping to support and enliven some larger center.
2. The center becomes precious because of it.

It is the second of these, above all, which is the key. Again, it is useful to look at the circles in the Japanese roof tile. They are not merely circles. They have become precious. A center occurs in space as the space becomes (or is made) precious. It becomes precious because it is helping some other larger center to exist, and to have life, and to be precious. But in the process, it itself becomes precious. So, suddenly, space is transformed. It starts out neutral. But as it becomes a stronger center, it is made precious. This preciousness is the vital core of every center.

12 / THE RECURSIVE CHARACTER OF LIFE

The nearly miraculous nature of the field of centers may now be almost visible. Let us consider the recursive nature of the field of centers once again through examples.

First, on this page, look at a fish pond illustrated below. Here we have the water, the waves, the fish, the plants, the overhanging bushes, the lilies in the pond, the lily leaves, the mud on the bottom, the caddis, the moss on the rocks, the slime in the water, the flow of water through the pond. Each of these centers, too, is brought to life, and has its life intensified, by the other centers. The fish themselves, for instance, live more intensely when the stream is flowing, so that the dissolved oxygen is constantly replenished. The shade, within the water, formed by the rocks and lily pads, allows the fish a place to cool themselves. The stream flow itself is brought to life, intensified as a center, by the eddies and turbulence at the edge, which make the pond.

Next, opposite, a front door with benches and plum trees. At the front door, we have the door, the steps, the seats, the fence, the purple tree, the space between the stoop and the street. The door makes the space more alive: the life of this space makes the benches more alive. The

purple tree makes the benches more alive: the protection of the fence makes the tree more alive, by shielding it from animals and passing cars.

In these cases the crux of the whole thing, then, is what happens when one center helps another come to life. The particular form the helping takes is different each time. But the fact that each time the helping occurs, and each time the centers being helped become more alive — these are the only common factors. That is the nature of the phenomenon of life. In a mechanistic frame of mind we seek a different mechanism for each example of helping — and focus mainly on the differences. However, I have gradually come to the conclusion that it is the fundamental similarity of all kinds of helping between centers

which is most important, even though this appears to be an un-analyzable concept which cannot clearly be expressed in terms of anything else.

In each case, the life which exists in each center itself becomes more intense as a result of the other centers, and their life, and the way that they become more intense. This effect is both geometrical and functional. It happens in the space. But it works in such a way that the common or ordinary life in the thing is what we see intensified.

Thus life itself is a recursive effect which occurs in space. It can only be understood recursively as the mutual intensification of life by life. The field of centers, which intensifies centers by virtue of their pure geometry, then creates life through this helping action in the geometric field.

13 / TOFUKU-JI

If it is true that the nature of order lies in some kind of unexpected substrate of space and matter where life, seen both as ornament and as function, appears as an awakening of matter — then we might expect to have at least occasional intuitions to support this point of view. From time to time, I have had glimpses of these intuitions.

I was visiting Japan in 1967. A friend, Tsune Sesoko, knowing my interests and my feelings about things, discussed my upcoming visit with two sixty-year-old calligraphers, who were then still part of the original Zen tradition, to get their advice. They told Tsune that I should visit a particular temple in Kyoto — a place called Tofuku-ji — “The only place left, where the old way is still visible, and understood.” I agreed to do it. I wrote the name down, and arrived in Kyoto, where I was to stay with another friend, a German architect. I told him of my desire to visit Tofuku-ji, and he said, “No, no, not Tofuku-ji, you must visit the greatest place of them all, the great Daitoku-ji.” I hesitated, said that I preferred to follow the advice I had been given, but he insisted

that it was not good advice, that he would personally take me to Daitoku-ji, and I would see for myself. I argued. To no avail. He insisted. Since I was his guest, I had to submit with good grace.

The next day we went to Daitoku-ji. I didn’t like it. Though beautiful in form, it seemed like an empty shell, a kind of tourist place, protected for tourist visits, no longer a living thing at all. For instance, beautiful paths, passing through moss gardens, were separated from the moss by heavy chains and little “Don’t walk on the grass” signs. After a few minutes, I couldn’t stand its artificiality, and decided that I must leave and find my own way to Tofuku-ji. I apologized to my friend, and went to find a three-wheeled bike-taxi.

I said the name To-fu-ku-ji syllable by syllable over and over again, until the driver understood. We drove far across town. I had no idea where we were. Almost an hour’s ride, out into the areas beyond the town, to the very edge, where the hills meet the town, almost out in the country. We stopped in a deserted place, outside a huge stone wall. The driver motioned with his

hand that he would wait there for me. I got out, passed through the walls, into the temple complex. Inside the atmosphere was astonishing: wild grasses, bushes, stones. It was like overgrown nature, almost completely wild, and yet I felt that it was cultivated, and in use. I walked about past giant, simple buildings, in a state like that of a working but slightly derelict farm, well kept, not perfect, but every part in use. After an

hour or two of walking around buildings, visiting a small sand garden, a wooden bridge over a gorge, and the main temple building — I found myself on a tiny path that seemed to lead away from the temple, up into the hillside. I followed this path up steps cut in the hillside, partly stone, set into the grass. The path went on and on, a shallow staircase, up into the hill, between two hedges. It was getting narrower and narrower all

the time. Toward the top, it got trapped between two low rambling hedges.

Suddenly it ended. To my surprise, I could not go further. The path just stopped. The

hedges closed. There was a small place at the top of the stair. I turned around and sat down. There was nowhere to sit, except on the top step, and that is where I sat, looking down on the

temple precinct, watching it, tired, happy to sit there, quiet, only the wind now instead of the sounds of temple business. As I sat there, a blue dragonfly came and landed on the step beside me. It stayed. And as it stayed I was filled with the most extraordinary sensation. I was suddenly certain that the people who had built that place had done all this deliberately. I felt certain—no matter how peculiar or unlikely it sounds today, as I am telling it again—that they had made that place, knowing that the blue dragonfly would come and sit by me. However it sounds now, at the time when it happened, while I sat on that stair, there was no doubt in my mind at all that there was a level of skill in the people who had made this place that I had never experienced before. I remember shivering as I became aware of my own ignorance. I felt the existence of a level of skill and knowledge beyond anything I had ever come across before.

I sat there for two or three hours—and then stayed in the temple all day long, filled, for the whole day, by my awe in the face of what these people had known, and by the beauty of

the place. Most of all I was simply shocked by the certainty that the people who made this place had done it with a level of skill far beyond anything that I had ever experienced—and that the grasses, the steps, the wind, the dragonfly, were all deliberately placed by their hands.

To this day, I have never again had such a shaft strike me. I have not seen again the possibility of such perfect human knowledge of nature. Every part of that temple, as I think back, was formed by the field of centers. Even in the little path I walked on it was crucial. Geometrically, structurally, each time the life came from some kind of sequence, from a layered structure which embodied a field of centers. On the path it was especially obvious, reaching finally to the top step where I met the dragonfly.

Every part of every place was slightly irregular. The sensation of nature waking up, and human beings helping to make it wake, was luminous, like a hum. I feel a heavy longing, remembering it, it was so vivid, so quiet, so perfect. Yet it changed my life to see it, and to walk through it.[23]

14 / THE AWAKENING OF SPACE

The ideas of this chapter fill out the structural conception of buildings which I began in chapters 1 and 2. In this conception life is something which exists in every event and building, even in everyday functional life — the burst of living — as a consequence of the structure of space.

In essence this conception is ancient. What is new is only the idea that it might be explained, and understood, in a structural form consistent with other scientific thinking. Even in modern physics, a similar idea, though strange to Cartesian ears, has been proposed by Eugene Wigner.²⁴ Similar views have appeared historically within the ideas of Buddhism and within the world-view of American Indians.²⁵ The Buddhist conception of the world, in which some degree of life exists in everything, has been put forward by innumerable ancient texts. It is summarized clearly and succinctly for one specific case by Francis Cook.²⁶ A more contemporary modern biological version of the same idea has been formulated by the Japanese biologist Imanishi.²⁷ A similar conception existed throughout Alfred North Whitehead’s thought and writing.²⁸

In this conception, each part of the world — building, stone, blade of grass, pane of glass, door, painting, brick, spot of color in a painting — has some life. In Whitehead’s view there is nothing which does not have some life. The possibility of life is inherent in matter. It is not an accidental thing which happens in organisms as matter gets highly organized. It is the very nature of order for matter to be alive. And of course, in this view, every building — like any other part of space — has life to a greater or lesser degree, and every part of every building has life to a greater or lesser degree.

I have tried in the last eleven chapters to present a structurally detailed account of this idea, to show how it might work. Within this framework, the idea that every building has its life — and that every part of every building also has its life — is a necessary and practical point of view, which can be understood concretely in terms of structure, and which follows naturally from the existence of living structure, the field of centers, and the intensity of this field, as a definite and real structure in space.

Even at this stage, the essential task of architecture — the nature of centers, and the task of making a single center — may still be far from clear. In order to understand it well, we need to recognize explicitly that each center is a kernel and spark of life in the fabric of space. That is, we have to understand, in an almost animistic way, that each center is a spot where space awakens, or comes to life — and that all function, all ornament, all order, comes into being, as the center takes on life whose potential existence is inherent in the space itself.²⁹

All this has intellectual consequences. If we want to make sense of the way that centers work, we cannot easily avoid the idea that space itself has the power to come to life — and that a center is an emerging spot of life in the material substance of space itself. This is disturbing, or at least surprising, because it is inconsistent with Cartesian mechanics.

But even if we might want to accept it, I have said little yet which can help us to understand it. What is this life which happens in space as space “comes to life”? What is the life of a center, which then multiplies and blossoms to form the life of buildings, ornaments — and perhaps even the life of living things?

Everything I have been talking about depends on this idea. It is this idea which forms the underpinning for the objective reality of wholeness, and for the basic idea that architecture can be understood in an objective way.³⁰ In appendix 4 of this book I have sketched the nature of space, as it might have to be understood mathematically, in order to bring this idea into the framework of modern physics.

In Books 2 and 3 and 4 we shall study this idea of “life” more deeply. We need to know how to measure it, how to estimate the degree of life inherent in a given center, and above all to find

out what it is. I shall try not only to provide an empirical basis for this idea, but also to show that it requires a new and surprising concept to make sense of it.

In Book 4, I shall suggest that ultimately we must understand the awakening of space, which occurs when a center gets more life, as a measure of the degree to which that center becomes associated with the human "I", or self. When a center arises, there is a feeling of space awakening, and the feeling of it is clear. The experience of this is so vivid that it is difficult to express. Anything that one can say about it sounds vague. Since it is awkward within the narrow Cartesian framework to recognize such an awakening, people suppress it. But the idea that space itself, like a bud opening to flower, is awakening somehow wherever a center occurs implies something strange about space.

When a building works, when the world enters the blissful state which makes us fully comfortable, the space itself awakens. We awaken. The garden awakens. The windows awaken. We and our plants and animals and fellow creatures and the walls and light together wake.

In order to make it possible to have an idea like this, we need to understand space as a material which is capable of awakening. This is what I shall later refer to as "the ground." The ground is just that "something" in the fabric of space which is capable of awakening. We may imagine it as lying behind the space or in the space or under the space conceptually. Or we may imagine it as the space itself, but then recognize space itself as something immeasurably deeper than the way we used to think about space in 20th-century physics.

NOTES

1. A general account of function in architecture, in a fashion which predates this account, is given in Christopher Alexander, Sara Ishikawa, Murray Silverstein, Max Jacobson, Ingrid Fiksdahl-King, and Shlomo Angel, A PATTERN LANGUAGE (New York: Oxford University Press, 1977).

2. Strangely, there are relatively few books on architecture which have dealt with this intensity of life and its relation to architecture, in a way that really sheds light on the architecture. One is Bruno Taut, HOUSES AND PEOPLE OF JAPAN, 1937 (Tokyo: Sanseido Co., Ltd, 1958). Another is John Ruskin, THE STONES OF VENICE (New York: J. Wiley, 1851) especially the extraordinary first chapter on the making and nature of a stone wall.

3. In the following examples, I shall not only show how centers necessarily work, but also explain how these centers will, in general, benefit from the fifteen properties that make them help each other. Some of these examples are discussed in A PATTERN LANGUAGE. In what follows I have given relevant page numbers for these references as APL. The discussion in APL is more "functional." At the time my colleagues and I wrote that book, the geometric-functional unity of space, based on the wholeness, was not yet fully clear to me.

4. APL, INTIMACY GRADIENT, p. 610.

5. APL, CORNER DOORS, p. 904.

6. See discussion of ceiling heights and room volumes in APL, CEILING HEIGHT VARIETY, p. 876, and THE SHAPE OF INDOOR SPACE, p. 883.

7. APL, WINDOW PLACE, p. 833.

8. The small altar-like niche in some traditional Japanese rooms, where ceremonial objects or beautiful objects are displayed.

9. APL, THE FIRE, p. 838.

10. See APL, WINDOWS OVERLOOKING LIFE, p. 889.

11. APL, POOLS OF LIGHT, p. 1160, for discussion of lights.

12. For other versions of the idea that ornament and function are merely versions of a single structure, see Cyril Stanley Smith, A SEARCH FOR STRUCTURE: SELECTED ESSAYS OF SCIENCE, ART, AND HISTORY (Cambridge, Mass: MIT Press, 1981).

13. Bill Hillier and Julienne Hanson, THE SOCIAL LOGIC OF SPACE (Cambridge: Cambridge University Press, 1984). Hillier and Hanson provide a successful and fascinating quantitative analysis of various social relations in villages and communities, and the way that social interactions are interdependent with the spatial organization in which they occur. Earlier writers on the relation between social events and space, often presented their analyses as if they were analyses of social events, and the way these social events depend on or are affected by space as their necessary background. In the view presented by Hillier and Hanson, they make it clear that, for them, and to make sense of the empirical results they have obtained, it is necessary to view space and social system as a single indivisible entity. Like Hillier and Hanson, I am convinced that the two must be viewed as a single thing, and I do not think a separation between social events and the space in which they happen is a helpful one.

14. Ibid., especially pp. 262–68.

15. Ibid., p. 26.

16. I should make it clear that I am not, of course, claiming that the artisans who made the column base on page 418 consciously used the idea of centers as I have formulated it. The same is true for the other examples which are to follow. What I am claiming is that these artisans were doing something which was essentially equivalent to the idea of intensifying the life of the centers. One form this may have taken in traditional cultures, is discussed in Book 4, chapters 4 and 5.

17. Chapter 5, throughout, and see especially the end of the chapter, pp. 236–42.

18. See R. Catesby Taliaferro, THE CONCEPT OF MATTER IN DESCARTES AND LEIBNIZ (Notre Dame: 1964), especially p. 33.

19. Denis Diderot, D’ALEMBERT’S DREAM (1769; reprint, New York: Penguin 1976), pp. 158–59.

20. A PATTERN LANGUAGE, LIGHT ON TWO SIDES OF EVERY ROOM, pp. 746–51.

21. No matter how many times I say it, the concept is nevertheless very hard for us to grasp — because we have grown up in the mechanistic positivistic way of thinking. It is really almost impossible. Even if I keep repeating it to myself, again and again and again, my way of thinking, which I have inherited from the last several decades, keeps making me think of the two things — function and geometry, function and ornament — as separate. But slowly, gradually, my mind is coming back together, healing itself, as I grasp the essential idea that there is not this separation, and that it is all just one kind of living space, and that my task is only to intensify its life.

22. This tile was a present from my associate and colleague, Professor Hajo Neis. Hajo got it from one of our subcontractors in Japan and gave it me for Christmas. Even by itself, it forms a very beautiful center.

23. I visited Tofuku-ji again in 1992. With enormous sorrow, I found out that by then, it had been modified for tourists, and was now of the same genre as Daitoku-ji. The atmosphere I have described in this chapter had largely disappeared. The little path was gone altogether, swallowed by a nearby development.

24. Eugene Wigner, “Limitations on the Validity of Present-day Physics,” in Richard Q. Elvee, ed., MIND IN NATURE: NOBEL CONFERENCE XVII (San Francisco: Harper and Row, 1982), pp. 118–33, especially 129–30.

25. For instance, the Cheyenne chief, Old Lodge Skins, in Thomas Berger’s novel LITTLE BIG MAN (New York: Dial Press, 1964): “But white people believe that everything is dead: stones, earth, animals, and people, even their own people. And if, in spite of that, things persist in trying to live, white people will rub them out” (p. 214).

26. Francis Cook, HUA-YEN BUDDHISM: THE JEWEL NET OF INDRA (University Park: The Pennsylvania State University Press, 1977).

27. Professor Kinji Imanishi, SHIZENGAKU NO TEISHO (IN SUPPORT OF GEOCOSMOLOGY) (Kyoto: 1983) and SEIBUTSU NO SEKAI (THE WORLD OF LIVING THINGS) (Kyoto: 1941).

28. See Lawrence Bright, O.P., WHITEHEAD’S PHILOSOPHY OF PHYSICS (London: Sheed and Ward, 1958).

29. So far, this still seems mysterious. You may say, This is all very well, but what is the life of a center? How do you measure it; how do you observe it? My answer at this stage would go something like this: Please, do not be impatient. Experimental and operational techniques are important. The experimental methods given in chapters 8 and 9 need to be developed. However, the first thing to establish is not the detailed operational measuring techniques, but the general idea of whether this seems a plausible and workable view of things. John Dalton proposed the existence of atoms and molecules, in about 1810, to account for arithmetic results which occurred in various chemical experiments. It was not until more than 100 years later that one could actually see atoms, or verify their existence by direct observation. In the same way, ecologists have recently introduced the idea of ecological “niches” to explain various structures in an ecological system. At the time this proposal was first made, what mattered was whether one got a roughly convincing idea of what it means, and whether it helps to understand things and make them more coherent and sensible. In a perhaps similar fashion, the idea that centers are structures that appear in space, and have life in themselves, is so startling and surprising as an idea, that the first thing we need to get clear is whether this idea has promise, and what we can do with it. Measurement, and detailed problems of objective evaluation of the type I have described in chapters 8 and 9, necessarily come a little later.

30. I have already shown, in chapter 4, that if we accept the idea of the life of centers as something real, then we can use it to explain how the life of other centers comes into existence recursively. In short, if we suspend our disbelief, and agree that there is such a thing, then we see how the lives of different centers depend on one another, and how the life of a building is created by the life inherent in its various component centers.

CONCLUSION

A FOUNDATION FOR ALL OF ARCHITECTURE

The scheme of things I have started to present covers all of architecture. The scheme starts with the concept of wholeness as something which exists in space, and with the idea of centers, the way that centers help each other. It goes on to the idea of living structure — the detailed ideas about the fifteen properties that allow centers to help each other, and the observation that this structure is pervasive in nature and in deeply satisfying man-made things.

This constitutes, I think, a complete and coherent intellectual platform on which it is possible to erect a sensible architecture. We have suffered, in the last hundred years especially, because the old roots of architecture—its sound pre-intellectual traditions—have largely disappeared, and because the lawless, arbitrary efforts to define a new architecture—a modern architecture—have been, so far, almost entirely without a coherent basis.

I am proposing a new basis, a platform which gives architecture new content and meaning. The most important thing about this platform I have presented is that it is based on what most people experience as true or real—it is rooted in observation. This empirical and factual nature makes it possible, in principle, for us to achieve agreement.

The confusion of the last hundred years in architecture has arisen, largely, because of the lack of a coherent basis which is rooted in common sense, in observation, and which is congruent with human feeling. The confusion has existed mainly because of disagreements about what should be done, what is worthwhile, what is it that we should aim for. These disagreements have not, on the whole, been pursued by experiment, or logical reasoning. The positions—modernism, postmodernism, organic architecture, the architecture of the poor, architecture of high technology, critical regionalism—the different positions—have been discussed much as one might discuss the latest clothing fashions. The absence of reasoned discourse has created, in the world, an architecture ruled by money and power and images.

All this has come about because, in the intellectual atmosphere of pluralism, celebrated in the 20th century, it has been easy to say what one believes, but nearly impossible to say what is good or true. Indeed, avoiding, at all costs, serious discussion of what is good has been the reason for the crumbling failure of the past century's architecture.

But it is exactly that question which cannot be avoided. A criterion for judgment is the core—the necessary core—of any architecture. A core of judgment cannot be created by shouting that one is right. Instead, a core of judgment must be found which appeals to the deepest instincts in everyone, so that we can say to ourselves, Yes, this is indeed the basis from which we ought to proceed, and therefore the basis from which we must proceed.

Obviously, I cannot prove by mere assertion that what I have written here constitutes such a basis. If the nature of living structure is to become the basis on which people approach architecture in the future, that will only be—can only be—because we recognize, by ourselves, and in our own terms, that it is a sensible way to go forward, and that it is congruent with our deepest sensations of art, and beauty, and justice, which affect the structure of buildings and towns.

My argument is simply this: the existence of wholeness is something real in the world, whether we choose to see it or pay attention to it, or not. It is a mathematical structure which exists in space. I believe that a holistic view of space—which shows how structure appears in space as a whole, as a result of local symmetries and centers—follows from careful observation of what exists.

I believe that what we call life in architecture and the built environment springs from this wholeness. Because space is of such a nature that symmetries and centers can arise in it, it follows that centers can help each other to become more and more alive. And it follows from that, that progressively more and more profound structures can exist in space. These are the structures we recognize in the great heritage of human art. It is highly significant that the same structures and the same structural scheme arise in nature. The structures we observe in nature also arise from the wholeness, and their life, too, comes from the root cooperation of centers, providing the foundation for the architecture I propose.

By illustrating the existence of living structure, I have shown, I hope, that the phenomenon of life is something greater, more profound, and more general, than what we have come to think of, and accept, as biological life.

In contemporary science, biological life has come more and more vividly into the intellectual picture. We have an emerging picture of biological and ecological systems as self-sustaining and self-creating networks. This picture is dynamic, promising, and marvelous. Yet it is still solidly mechanistic in nature.

I believe that I have shown that this picture is simply not deep enough to be true. Fueled by questions which arise in art and architecture, and inspired above all by the yearning to create great buildings, better buildings, buildings which have life in them, I have tried to draw attention to the idea that life, as a phenomenon, occurs not only in living organisms and ecological networks. It is something, a quality and a structure, which occurs in all kinds of places and systems in the world, both inorganic and organic.

I have tried to suggest — to prove — that life is a phenomenon which is more profound than a self-reproducing machine, that it attaches to the very substance of space itself. As such, it is capable of laying a foundation for all of architecture, for the construction of a living world.

This foundation is more general than the one provided by contemporary biology, because it suggests that even in static structures, in stones, in rooms, in water, in sand, even in color, life can occur, life does occur, and that this life, which occurs in speechless stones and concrete, is something that goes to the very root of human existence.

I have suggested that living structure lies at the core of all life. This living structure is in the very mathematics of space. It is a discernible, countable, and measurable quality, which arises—for structural reasons that concern only the appearance of centers, all of them differentiated structures—in space itself.

The living structure I have described is highly specific and real. Whether or not it is present in a particular part of space, and to what extent it is present there, are questions of fact. We are assured, nearly, that when this living structure is present in a particular part of the world, we react to it; it makes us feel alive merely to see this living structure or to be near it. It is, at least to an approximation, the key to good architecture—something that was held for so long to be a matter of intuition, beyond analysis. But it is definable, and it is accessible to analysis.

The future of architecture can be changed, fundamentally, by an appreciation of living structure. If we choose, consciously and intentionally, to create this kind of living structure in the streets and buildings of our world, we have a good chance of being able to create a true living world, something of the same depth that traditional builders and craftsmen were able to accomplish.

As I have suggested in chapter 10, there is reason to think that the existence of this living structure—wrapped in culture, based on culture, and mixed with culture, to be sure—is the substrate which provides us with our freedom, with the ability to be free in ourselves. Thus living structure has vital practical and social consequences. We may say that, for the sake of our own welfare, the world must be made so that it contains, and is built from, living structure.

In Books 2 and 3, I shall discuss the ways in which living structure can be created. We need to learn how living structure is to be created and sustained. It is not easy. And there are only certain restricted methods, or processes, which typically create living structure.

To have a practical theory of architecture which can create living structure in the world, we shall find a need for processes which hark back to ancient prototypes of process, and which yet point to the far distant future—a future possibly remote from our present abilities and sensibilities—and to an age when the creation of living structure may be understood by all of us as the most fundamental task of human beings.

The living structure is something which closely resembles ancient and primitive forms. It is not modern, it is not classical. It is derived, as it were, from the deepest and most ancient archetypes. Yet like the Golden Gate Bridge in its time, it also resides in the most modern technology. Substance is to be formed from the material of space in such a way that in it, we recognize our own souls. And this stuff, its matter, its organization, is to provide the stylistic, and practical, basis for a new architecture.

The living structure contains everything of importance about a building. Above all, it contains the functions of the building. The building which works best, I maintain, will be the one which has living structure to the greatest degree.

Further, and perhaps most surprising of all, this living structure is somehow connected to, wrapped up in, our own selves. The deepest living structure is that which reflects the deep self of all of us, and of each of us as individuals, most profoundly.

This is a new way of looking at architecture. The intellectual foundation of this vision is the idea that space itself, matter itself, has life in varying degrees. There is a convergence of function, geometry, and feeling in space; this space is conceived as a living fabric that—through its structure—encompasses these things. Space does not merely contain living structure. Space has life, to a greater or lesser degree. It is the space itself which resembles self, which functions, which works, which has living structure in it, and which has life. The life which appears is an attribute of space itself.

The architecture which follows in Books 2, 3, and 4 is based on a conception of the world in which the air we breathe, the stones and concrete our city streets are made of, all have life in them, or not; all have life, anyway, in varying degrees. Our job, as architects, builders, citizens, is to create this life in the air and stones and rooms and gardens—to create life in the fabric of space itself. This is not merely a poetic way of talking. It is a new physical conception of how the world is made and how it must be understood.

APPENDICES

MATHEMATICAL ASPECTS OF WHOLENESS

AND LIVING STRUCTURE

APPENDIX 1

SUPPLEMENT TO CHAPTER 3

DEFINITION OF THE WHOLENESS

This is the first of a series of technical appendices, which together seek to lay out the groundwork for my claim that what is reported in this book is not merely a new way of understanding architecture, but also a small step to a new way of understanding matter itself.

The wholeness, $W$, is a feature of physical space which appears everywhere, in every part of matter/space. It is, I believe, susceptible to a clear mathematical definition and is characterized by a well-defined mathematical structure.

Consider any region of space, $R$. We may, for convenience, impose a grain or mesh on the space, so that the number of points is considered finite, not infinite. Let us say that $R$ contains $n$ points. In cases which model the real world, there is usually some "coloring" or differentiation of type or character among the $n$ points of $R$, so that the region $R$ has a visible or identifiable structure. The simplest coloring which produces a structure is a coloring in which some points are black, others white. In the two-dimensional case, $R$ would then be a drawing in which we see some particular object. In the case where the coloring is not abstract, but material, points may be assigned labels corresponding to actual physical materials; for example, they might include solid and void, or various physical or chemical attributes. The region $R$ is thus intended to represent a part of the real world in its overall geometric form and organization.

I shall now explain how to construct a wholeness $W$ on the region $R$. Within the region of space $R$, which contains $n$ points, there are $2^n$ distinguishable subregions. Call a typical one of these subregions $S_i$. In what follows, we construct $W$ by recognizing that there are different relative degrees of coherence which may be observed in the different subregions $S_i$.

It is a common fact of experience that we see regions of space which have different degrees of

coherence. For example, we consider an apple to be coherent. If we consider the set of points that consists of half the apple, we shall probably consider it less coherent than the apple as a whole. In a similar fashion, the pips of the apple are coherent. And this idea of relative coherence does not only apply to sets which are in some sense complete wholes. A portion of the apple which includes the core plus the hull that houses the pips is moderately coherent. A random section of the middle of the apple would be less coherent, but still coherent in some degree. A disconnected set of points, including bits of skin, core, pip, etc., mixed up, would be still less coherent.

Although it may be impossible to construct a complete rank order on all the different possible subregions, it is clear that our intuition does typically assign some relative degree of coherence to each different subregion. We do recognize coherence in the world. This coherence, is just that attribute which I have referred to throughout Book 1 as life. The structure of the wholeness $W$ relies on the fact that we shall make such distinctions of life explicit, and use them to erect a structure.¹

To make the idea of different degrees of life explicit, we introduce a measure of life $c$, on the subregions of $R$. Call each possible subregion of $R$, $S_i$, where $i$ ranges from 1 to $2^n$. The life of the $i$-th subregion $S_i$ is then to be $c_i$. Each $c_i$ is a number between 0 and 1, and every subregion of $R$ is to be given its measure of life. The most coherent regions have a $c_i$ which is close to 1, the least coherent regions have a $c_i$ which is 0 or close to 0.²

There are many different possible measures of life $c$, which may serve this purpose. Some $c$'s may be measured empirically, others may be calculated mathematically as functions of the structure in $R$. In the end, I believe that there is an objective measure of life, which may be determined empirically, for any given region within a

given wholeness. Experimental methods of finding this $c$ are discussed in chapters 8 and 9. However, it is also possible to define various approximations to this empirical life, which may be obtained by calculating the life of $S_{i}$ as a function of the internal structure of $R$ or $W$. An example of this type is given in the following appendix. For the rest of this appendix, I shall not be specific about the way in which $c$ is going to be measured or calculated. In all that follows, regardless of the specific definition of $c$, $c_{i}$ is simply to be understood as some measure of relative life, in which the most coherent regions $S_{i}$ have a life 1, the least coherent have a measure 0, and others have intermediate values.

I call the most coherent subregions of $R$, centers. A region will be considered more or less centered according to its life. The most coherent subregions $S_{i}$, which have a $c_{i}$ close to 1, will be called the centers of $R$. Even among the centers, there are still degrees of relative life — some are more coherent than others — but all of them establish, through their life, a phenomenon of centeredness in space.

To further simplify our understanding of $W$, we may make an approximation in which we ignore most of the highly incoherent regions of $R$, (the bottom ninety-nine percent of the rank order), and keep only those few regions which are centers with significant life. The remaining structure is much smaller than $W$, but far more manageable than $W$. We can still call it $W$, but understand it as an approximation. In this approximation, the wholeness $W$ is to be understood as a system of centers, containing the most coherent regions in $R$, rank-ordered according to their relative degree of life. For example in a real region of space, studied at a mesh which gives it a million points, $W$ contains $2^{1,000,000}$ subregions. Of these possible subregions, the wholeness might be sufficiently well defined by 1,000 subregions — which would be a tiny proportion (far less than 0.000000000000001 percent — actually 1 in $2^{999,990}$) of all the subregions of $R$. This drastically reduced system $W$, although based on a tiny fraction of the subregions of $R$, still has 1,000 centers

rank-ordered according to their relative life, and may still nicely summarize the wholeness of the region $R$.

I define the wholeness $\mathbf{W}$ as the system which is created by the region $\mathbf{R}$, together with the measure $\mathbf{c}$ and all those subregions which have measure more than some threshold and thus qualify as centers. For all practical purposes, the wholeness $\mathbf{W}$ is created by the interaction of the geometry of the region $\mathbf{R}$ and the rank order which is created on the centers of $\mathbf{R}$ by $\mathbf{c}$.

The nature of the wholeness $W$ may be clarified by considering it as a generalization of the topology of a figure. The idea of topology may be summarized like this: it depends on the intuition that the character of a particular multidimensional configuration $R$ depends in some way on the system of those subsets of $R$ which are connected. If we give all the connected subsets the measure 1, and the remaining (non-connected) subsets the measure 0, then the sets of measure 1 establish the connectivity of $R$.

Although the subject of topology is rich and profound, it all originates from this simple intuition: namely, that the character of a configuration is given by the particular system of subregions that are connected, and by the way these connected subregions overlap and lie within each other.

The work which I am describing in this appendix is based on a similar, though more complex, intuition. This intuition says that the order we perceive in any region $R$ always depends essentially on the relative degrees of life which exist in the different subregions of the region $R$.

But unlike the topological case, where subregions have only two possible degrees of coherence (0 if not connected, and 1 if connected), we now contemplate a system in which the various subregions of $R$ can have a range of life. Some sets may have life 1, others might have life 0.9, others a life 0.5, others a life 0.001, and others a life 0.000001.

Note that this argument requires that we accept the intuitive idea that different subsets (or subregions) of $\mathbf{R}$ do indeed have different degrees of life.

This assumption, which corresponds to intuitive observation of degrees of life as discussed in the text, does not have a formal counterpart in present measurements or observations that exist in physics.7

The wholeness $W$ is more general than the topology, and much more interesting, since it identifies and distinguishes configurations in the ordinary world of real objects. Again, we start with a certain set $R$. Instead of merely having two classes of subregions — open and closed, as in the case of topology — we erect a measure of life on the different subregions of $R$, and we recognize that there are different degrees in the life or connectedness of the various subregions.

NOTES

1. The idea of representing all space as a system of nested centers was, I believe, first formulated by Alfred North Whitehead, in a paper whose reference I can no longer find on the “Boolean algebra of sets.” Whitehead proposed a system of coherent entities which he called organisms. His general idea was that all of reality could be understood as a system of “organisms” in space — the organisms being nested and overlapping. Whitehead’s “organisms” are, I suspect, much the same as the entities which I describe throughout this book as centers.

2. The subregions $S_{i}$ are technically subsets in space — they are not necessarily connected, and do include points which are distant from one another without the intervening space.

3. See appendix 2, page 449, and appendix 6, page 469, where local symmetry is used as a measure of life.

4. Suppose we have some figure $R$ (a Möbius strip, or Klein bottle, for instance). The topology of the figure $R$ is defined by a system of connected subregions of $R$. The set $T$, which includes all the connected subregions of $R$, is the topology of $R$. As we know, this system $T$ allows us to identify certain particular configurations, which are determined by the relative connectedness which exists among their subsets. Loosely, we may say that the overlapping of subsets in $T$ defines the way in which the figure $R$ is connected, and thus creates what we intuitively grasp as its topological connectedness.

5. Combinatorial topology uses this essential intuition to describe approximations to a given figure, by a finite covering in which the sets of measure one are the simplicial complexes of $R$. General topology extends this intuition to the infinite case, where the sets of measure one are then defined as open sets, while all other sets are given measure zero. For definitions and surveys of elementary topological concepts, see, for example, L. S. Pontryagin, FOUNDATIONS OF COMBINATORIAL TOPOLOGY (Rochester, N.Y.: Graylock Press, 1952), or M. H. A. Newman, ELEMENTS OF THE TOPOLOGY OF PLANE SETS OF POINTS (Cambridge: Cambridge University Press, 1951).

6. The topological invariants (groups and so on) are really nothing but shorthand ways (albeit very profound ones) of writing down the different possible kinds of connectivity.

7. See the extended discussion in chapters 8 and 9. The fact that, in any given configuration, some sets are more salient than others has been carefully discussed by the gestalt psychologists Max Wertheimer, Kurt Koffka, and Wolfgang Köhler in a series of publications. See references in chapter 3. It has also been the subject of recent mathematical work by René Thom, SEMIOPHYSICS: A SKETCH (Redwood City, Calif.: Addison Wesley, 1990), 3–6, 41–43.

APPENDIX 2

FURTHER SUPPLEMENT TO CHAPTER 3

A DETAILED EXAMPLE OF THE WHOLENESS (W)

I hope that, in the future, mathematically inclined readers will develop the theory of wholeness by giving explicit mathematical descriptions (by computer methods or others) of the way the wholeness works. Nikos Salingaros and others have begun this work. For such readers, who would need to be very precise about the detailed meaning of $W$ as given in appendix 1, I include this second appendix as a supplement to the first. It contains a single worked example. The example is intended to illustrate the abstract definitions of $W$ in a concrete manner by calculations worked through in complete detail.

This example is, of necessity, very small indeed. The nature of $W$ relies on the relative life of the subsets of a given pattern $R$. If $R$ contained 100 points, say, there would be $2^{100}$ possible subsets, all potentially playing a role in $W$. To examine these subsets in detail would be an unworkable labor. Yet in order to understand what $W$ really is, and what it means, I believe it is necessary to see clearly what the relative life of the different subsets is like, set by set, in an actual worked example.

I have therefore chosen a very small pattern (illustrated on this page) which, at the level of approximation I choose, has only seven points. It therefore has only $2^7 = 128$ possible subsets, a small enough number to allow us to look at all of them, visualize them, and discuss them. The example I have chosen has one other advantage. In experiments I did with colleagues at the Center for Cognitive Studies at Harvard, in about 1960, this pattern and several others like it were studied experimentally. Published data describe the relative coherence of this pattern, compared with others. These data have been summarized in chapter 5. Other published data describe the way different subjects saw the pattern and its similarity to other patterns. These data are summarized in appendix 3. Using this example, it is therefore possible to see how the wholeness $W$, as defined by theory, allows us to make concrete and successful predictions about the real empirical impact of its wholeness.

Thus the example is both small enough to allow detailed scrutiny of its subsets and centers and has a background of empirical study which allows us to compare the results of theory with the results of experiment.

The pattern illustrated at the bottom of this page is a strip seven cm long, one cm wide, lying on a gray background and containing seven squares one cm by one cm, each square colored either black or white. In the case of the pattern illustrated, three of the squares are black, four are white. I will call this pattern $R$. Though it is constructed from seven squares, divisions between adjacent white squares are not shown.

To get the wholeness of the pattern $R$, we need to look at all the different subsets of $R$, and examine their relative life. The wholeness $W$ is the system consisting of the most coherent subsets of $R$. To simplify examination of the subsets, we use the very crude one cm mesh to divide up $R$ up into "points," which are actually squares 1 cm by 1 cm. In this version, $R$ then has seven points. This allows us to get a first approximation of the wholeness $W$ for $R$.

Since there are seven points in $R$, there are $2^7$, or 128 possible subsets $S_i$ of $R$. Only a few of these subsets are "coherent" in some sense; and it is these coherent sets taken together, as a system, which form the wholeness of $R$. To simplify the task of examining the subsets of $R$, let us throw away all those sets which have disconnected points [like (13) or (27)], and consider only the connected sets of points like (123) or (3456) [I use the numbers to identify points reading from left to right, so that (13) is the set consisting of the first and third squares in the pattern]. Of the 128 possible subsets, 100 are disconnected. I disregard them because they are so weak as centers that they play no significant role in the wholeness. I also disregard the seven sets consisting of individual points. The remaining twenty-one subsets of $R$ all have more than one point and are connected. There is one of length seven, two of length six, and so on down to six of length two. These twenty-one connected sets are the most interesting sets in $R$, and do the most to contribute to the wholeness of $R$.

Let us consider some of these connected sets. Consider, for example, the set (12), which has a black square on the left and a white square next to it. Within the pattern $R$, this set has no marked life or coherence and plays little role in the gestalt of $R$. On the other hand, the set (1234) consists of two black squares forming a sandwich around two white ones in the middle. This set has strength as a center. It is clear that

it appears in $R$ as a visible element or sub-whole and it forms a strong center in $R$. This, therefore, is one of the sets we want in $W$.

We could examine each of the 21 connected subsets of $R$ one by one, and decide on its life, or relative life, to determine whether it forms a center. If we did this, the system of all the coherent sets—the centers—would give us $W$.

Instead of doing this, which is laborious even in this simple case, I can get an approximation for $W$ by choosing a mathematical function which gives us an approximation to the life for each subset. One simple example of such a function is $c_{symm}(S_i)$:

$$ c_{symm}(S_i) = \begin{array}{l} 0 \text{ if } S_i \text{ is not connected} \ 1 \text{ if } S_i \text{ is connected and} \ \text{bilaterally symmetrical} \ 0 \text{ if } S_i \text{ is connected and not} \ \text{bilaterally symmetrical} \end{array} $$

This function is based on the local symmetry of the subset. It gives each connected symmetrical subset the measure one, and all other subsets measure zero. Expressed differently, it says that the strongest centers of $R$ are the locally

The pattern R has, within it, the eight centers formed by local symmetries, as shown above. To a first approximation, the system of these eight centers together, with their embeddings, constitute the wholeness W for the pattern R.

symmetric connected sets. $^{12}$ The wholeness $W_{symm}$ for $R$, defined by this artificial measure of life $c_{symm}$, is shown in the diagram below. As we see, $R$ contains just seven symmetrical segments more than one square long: they are shown below. Approximately, we may say that these seven symmetrical segments are the strongest centers of the pattern, and this system of seven centers is the wholeness $W_{symm}$ for this pattern.

This particular function $c_{symm}$ is significant because, roughly, it does indeed correspond to the centers we experience in the wholeness. For instance, the set (12) mentioned above which is not coherent, is asymmetrical. The set (1234) mentioned above, which is coherent, is symmetrical.

And the wholeness $W_{symm}$ described by this measure of life $c_{symm}$, even though simplified, turns out to have surprisingly good predictive power. As I have mentioned in chapter 5, the perceived life of the 35 patterns similar to $R$, as measured experimentally by various measures of cognition, memory, speed of perception, ease of description, etc., has been determined. The pattern $R$ is about eighth in the rank order of the 35 strips which were examined. It is less coherent than some, more coherent than others. As it turns out, the particular version of the wholeness $W_{symm}$, determined by the symmetry measure, predicts this experimentally determined rank order (in comparison with other patterns) extremely well—not perfectly, but extremely well. Thus $W_{symm}$ can predict, and explain to some degree, the way these patterns are experienced cognitively. $^{13}$ In appendix 3, we see that it also gives a first approximation to the similarities in wholeness that different observers experience.

However, in spite of these empirical successes, it is important to recognize that $c_{symm}$, the

local symmetry of sets, is only an approximation, and will not perfectly identify the naturally occurring centers in a pattern. For example, in the pattern (WBWBBWW), the segment (2345), which goes (BWBB), is clearly perceived as a dark lump with a white middle, and hence as a center in the actual pattern. Yet it is not symmetrical, and will therefore not be identified by $c_{symm}$. Thus $c_{symm}$ makes mistakes. It will not pick out all important centers.

Further, in the pattern $R$ (BWWBWWB), the set (1234), with its strong black-white contrast, is actually a stronger center than (23), which is just a white bar. However, both are symmetrical and $c_{symm} = 1$ for both these sets. In the real $W$ for $R$, $c_{2345}$ should therefore be bigger than $c_{23}$. The $c_{symm}$ is inaccurate in this respect. Otherwise stated, $c_{symm}$ does not correspond, exactly, to the rank order of life of the subsets as they occur in $R$, and therefore only constructs an approximate $W$, which only approximates the actual $W$ that exists in the world.

Even so, it is significant that $c_{symm}$ gives such a remarkably good approximation. It predicts, correctly, the relative overall life of different black and white patterns, as measured experimentally by Alexander and Carey. $^{14}$ And it predicts correctly the overall similarities among black and white patterns, as measured by Alexander and Huggins. $^{15}$

As I have said, the mathematical structure $W_{symm}$, though sophisticated and precise, is still not quite right, and must be viewed as an approximation. To get closer, we could, for example, use a more sophisticated mathematical measure — $c_{second order symm}$ — which calculates, for each of the 28 connected subsets, how many local symmetries it contains, and therefore what its expected life might be. This would then be fed in to form the measure for a new more complex $W$, which we might call $W_{second order symm}$. This would be complex and hard to calculate. And even this second more complex $W$ would still only be an approximation to the real $W$, $W_{true}$, which depends on the empirical degree of strength of the various centers in the pattern, as perceived.

Other more complex arithmetic functions to use as possible measures for the life of centers have been proposed by Salingaros, and by Klinger and Salingaros.¹⁶ The measures they propose include the local symmetry, but add other features into the computations. They get very good agreement with empirical determination of relative life in different buildings.

Thus we have many possible ways of trying to get $W$, empirically and mathematically, by choosing different functions to approximate the degree of life of different centers. Ultimately, as in mathematical physics, one might arrive at a deep enough understanding so that a mathematical $W$ could be defined which would be a very high-order approximation to the true wholeness and would, to all intents and purposes, then serve as a readily calculable $W_{true}$.

Using computer techniques, it is also possible to contemplate a recursive function, which works iteratively. We would use a certain measure to calculate a first approximation of $c_i$ for all the sets. We would then feed this back, and use this first iteration, as a basis for calculating a second iteration, and so on, for as many iterations as we wish. This technique would come close to the recursion contemplated in the fundamental mathematical definition of the degree of life of any given wholeness that is specified in chapter 4.

I hope this example gives the reader a feel for the nature of $W$. The ideal, which we should perhaps call $W_{true}$, based on the real relative strengths or life of different subsets, is difficult to obtain, because it would require a very large number of empirical measurements on all the different subsets of $R$. Nevertheless, it is this ideal $W$ which is the wholeness, as it occurs, and is, ultimately the subject of this work. However, as we have seen, even mathematically constructed approximations like $W_{symm}$, using symmetry and other measurements on subsets, may give us very useful and surprisingly accurate approximations to the wholeness. Like any scientific models, they are imperfect, but may nevertheless give considerable insight into the actual behavior of the structures being studied.

NOTES

8. Experiments on the way people see these and other black and white patterns were first published in Christopher Alexander and Bill Huggins, “On Changing the Way People See,” PERCEPTUAL AND MOTOR SKILLS 19 (1964): 235–53.

9. Experiments on the perceived relative life of the black and white strips were first published in Christopher Alexander and Susan Carey, “Subsymmetries,” PERCEPTION AND PSYCHOPHYSICS 4, no. 2 (1968): 73–77.

10. Chapter 5, page 189.

11. Appendix 3, page 456.

12. We may say that, according to this measure, centers are defined as sets whose $c_i = 1$.

13. As given in Alexander and Carey, “Subsymmetries.”

14. Ibid.

15. As given in Alexander and Huggins, “On Changing the Way People See.”

16. Nikos Salingaros, “Life and Complexity in Architecture from a Thermodynamic Analogy,” PHYSICS ESSAYS (1997, Vol. 1, no. 10), 165–173, and Allen Klinger and Nikos Salingaros “A Pattern Measure,” ENVIRONMENT AND PLANNING B: PLANNING AND DESIGN (2000, volume 27) 537–47. Division of Mathematics, University of Texas at San Antonio, San Antonio, Texas, and Department of Computer Science, UCLA, Los Angeles.

APPENDIX 3

SUPPLEMENT TO CHAPTERS 3 AND 4

COGNITIVE DIFFICULTY OF SEEING WHOLENESS

It is not always easy to see the wholeness which exists in the world. Our verbal structure can mislead us and make us pay more attention to certain features of a situation than to others, so that we then see a biased or distorted picture of the wholeness which confronts us, not the wholeness itself.

I have suggested in chapter 3 that the human process of perceiving a distorted wholeness is responsible for many ills of architecture. A similar suggestion was made by David Bohm. Thus: “Of course the prevailing tendency in science to think and perceive in terms of a fragmentary self-world view is part of a larger movement that has been developing over the ages and that pervades almost the whole of our society today. . . . As has been indicated, however, men who are guided by such a fragmentary self-world view cannot do other, in the long run, than to try in their actions to break themselves and the world into pieces. . . .”¹⁷

Indeed, we can see that the wholeness of the world is being misunderstood, or not perceived at all, simply from the building construction we see in so many places in our towns and countryside, and from the violent way it so often violates the wholeness which exists, thus ruining both landscape and townscape. The overwhelming problem, with modern building, is that it often fails to enhance, support, the wholeness which exists. That is why we are so dismayed by it, and why it seems so uncomfortable, so far at odds with life.

This topic is taken up at great length in Book 2—especially chapters 13 to 15. Indeed, the whole of Book 2 may be understood as an essay which describes the process which is needed, in the world, to make sure that each act of design, planning, or construction, is consistent with, and contributes to, the wholeness which exists. That is the whole ballgame. That is the basis of life.

But the problem is, if we cannot see the wholeness which exists in the world, then of course we cannot take actions which are consistent with the wholeness which exists.

I was astonished, many years ago, to find out, in the course of an experiment I was doing with Radcliffe students, that most of them did not see the wholeness of simple patterns. They saw, instead, a distorted picture of these patterns, viewed them with arbitrary intellectual devices rather than responding to the deeper wholeness that was present in them. I found out, too, that it took immense effort to dissuade them from their distorted cognition, and to help them to see wholeness as it is. I shall briefly summarize the results of my experiments.¹⁸

In the base experiment, I used the same 35 black and white patterns described in chapter 5. In this experiment, I asked people to play with the strips on a gray board and group them according to their similarities: to lay them out in such a way that similar ones were together.

It turned out that the subjects in our experiments (Radcliffe students) always made versions of two broad kinds of layout: one (upper illustration on the following page) in which the strips were grouped by reading the strip left to right; and one (lower illustration) in which the strips were grouped by their overall pattern or configuration.

In the upper layout, the patterns are grouped as they might be in a library, by reading the pattern from left to right. The first column contains all those which start with two black squares; the next column all those which start with one black square; and so on. This is certainly one rational way to group these patterns, and very much in keeping with the way our minds have been trained.

In the lower layout, the strips are grouped by their pattern. Those with similar structure or similar configuration as a whole are placed near

each other. For instance, on the left, one sees all those patterns with a staccato pattern made of many small units; on the right, one sees a group of all those with a slow, lazy pattern of long bars. All those which contain the figure two black, one white, and then one black, whether this figure is left to right, right to left, at the end of the strip, or in the middle, are grouped together.

The second layout is based on wholeness. The first layout, on the other hand, is based on an arbi-

trary way of classifying the patterns, but not on their wholeness. Bill Huggins and I discovered in 1960 that among Radcliffe students most did not see the wholeness, and could not see the wholeness. Moreover, that it was extremely difficult to get them to change their perception so that they could see the wholeness.¹⁹ On the other hand, in other experiments, we found that young children routinely saw the wholeness, and that mentally retarded people, too, usually saw the wholeness.²⁰ Only the adult and highly educated Radcliffe students grouped the patterns by reading them left-to-right, thus ignoring the wholeness of the patterns.

Let us first see what it means to say that the second way of grouping the patterns is based on their wholeness, while the first way of grouping them is not. Consider the black and white pattern described in appendix 2, which goes BWWBWWB. In the wholeness of this pattern, the following sets are strongest: The sets BWWB and WWBWW are strongest. The sets WW, and B . . . B . . . B are slightly less strong but still very important. The system of these strong centers defines this particular wholeness. A holistic perceiver sees this pattern more or less as it is, and therefore groups this pattern with others which have similar configuration, that is, with other patterns in which a similar system of centers occurs: for example, the patterns BWWWBWB and BWBWWWB which also contain long white bars trapped between black squares.

But a perceiver who looks at the pattern by reading left to right in the sequential mode is not seeing the structure of the wholeness, but is instead paying attention to some different structure in which the relative strengths of different centers (the crux of the wholeness) is distorted. She chooses to see sets B, BW, and BWW at the left-hand end as strongest—not because they actually appear strong, but because she has decided to make them strong in her mind, so as to use a kind of “alphabetical” classification system.

Huggins and I were very surprised indeed to discover that 80 percent of our Radcliffe students—highly educated, intelligent people of

the 1960s — focused on an arbitrary and, I would suggest, insignificant aspect of the patterns.

It might be argued that the two groups of perceivers both chose aspects of the patterns which were valid, and that their two modes of perception are equally valid. It might also be argued that the perceivers who chose to arrange the patterns on the basis of left-right reading might have been perfectly able to see the wholeness, but simply chose to use another aspect of the patterns as a basis for sorting them.

But I believe this experiment suggests that most educated people do not see the wholeness of the world around them. Thus our experiment was merely a laboratory version of a far more serious cultural and societal problem: the fact that in a culture which is based on mechanistic views of reality (especially in the culture we have today, which is not only mechanistic but also highly verbal) the atomistic/sequential view of reality is typical, and people's ability to see wholeness is, in general, very much diminished.

This was not always so. In many so-called primitive societies, holistic perception was the normal mode of perception. There is considerable evidence that people from so-called traditional cultures — the cultures that we often admire for their ability to produce great art — had a mode of seeing in which they saw things in their wholeness. Our notion that they were primitive, and that we are sophisticated, is mistaken, I think, when we consider that they saw the all-important wholeness correctly, while we so often fail to see it.

Children are also better at seeing the wholeness than adults. This is, I believe, because the wholeness comes to us, it is visible at all only when our minds are open. It is words, and learning, which have the power to distort the wholeness, and to prevent us from seeing it. If we have notions, or theories, or preconceptions about the parts, we focus our minds on individual things, and fail to see the system of centers in its balance as a distributed, distended unity.

More worrying, it appears that it is not easy for an educated, “modern” person to recover her or his natural holistic perception. In a second se

ries of experiments which Huggins and I also did with Radcliffe students, we found out that it is extremely difficult to teach a person to see holistically once she has been educated to see sequentially. We tried to devise forms of training which would move a person's perception toward perception of wholeness. Since we had an objective method of testing the way that a person sees the black and white strips, we could test people, after exposing them to various types of training, to see if their ways of seeing really had shifted toward the holistic mode.

Over a period of months, we tried many different training techniques. We asked people to play with the patterns, build things with them, look at them from a holistic point of view, close their eyes and dream about them. None of these things worked. These techniques had virtually no effect. Only one technique that we ever found successfully changed a person's perception toward holistic.

The successful technique went like this: the subject was shown one of the thirty-five patterns and allowed to look at it for a few seconds, until she knew which one it was. She was then shown a large rectangular array of thirty-five different patterns jammed up close to each other in a very confusing way, and without any visible order to the arrangement. This array was flashed on a screen for just one second. During this one second, the subject had to find the particular pattern she had been shown. If she succeeded, she won a nickel (in 1960, enough to buy a cup of coffee). But it was hard to win the nickel. The task is very hard, roughly comparable to the difficulty of finding a single word on a page, in one second, without having time to read even a single line.

Under these conditions, looking at the patterns one by one just doesn't work. There isn't time to do it. But under the pressure of the experiment's one second deadline, doing it again and again, subjects gradually found a way in which they could find the pattern they were looking for, in the one second they had available. What they did, and had to do, to make it work was to gaze in a blank, unfocused fashion at the

whole array, trying to allow themselves to be blank, receptive, and to see the board all at once. Try it yourself. In this receptive mode, you have to move "back" mentally, away from the patterns, and then begin to see differently: you almost have to let your eyeballs move backward in your head. Mentally you back away from the screen, and open your eyes very wide, so you are not looking for anything in particular, but see everything. This forces you to see "the whole."

In this state, even in the short time of one second, you can often "see" the one you are looking for. You don't see it perfectly, because you are not looking at it. But you are aware of it, within the field as a whole. It is a state of perception in which you are unfocused and therefore extremely passive and receptive: then the pattern you are looking for almost seems to come to you. You don't search for it. It comes to you.

More than half of the people who were exposed to this high-speed search technique then learnt to see holistically, where only twenty percent had seen holistically before. Apparently, this exercise did enough to change the taught and "verbal" or conceptual form of looking at patterns, and replaced it with a holistic way in which people really saw the wholeness that was there.[21]

This experiment is very instructive. It tells us that the ability to see wholeness as it is requires an unfocused view in which we do not select what we pay attention to or force attention in a certain mental direction. Instead we see, watch, drink in the configuration of the wholeness which we see before us.

As I have stated in chapter 3, words, concepts, and knowledge all interfere with our ability to see wholeness as it is. To see wholeness accurately, we must not pick out those artificially highlighted centers which happen to have words as names, since these are often not the most salient wholes in the real wholeness. What we must do instead is to watch, quietly, receptively, and in an unfocused state, for those centers which are most salient in the real configuration as it is.

A similar experiment, also trying to help people abandon their focus and attention and

see reality as it is, was described at great length by the French psychiatrist, Hubert Benoit, in LET GO.²² Again, in that experiment, Benoit demonstrated that by abandoning our adherence to verbal structures, we come closer to seeing reality as it really is. The reality he describes, the Zen reality, is essentially the same as the wholeness I describe.

NOTES

17. David Bohm, FRAGMENTATION AND WHOLENESS (Jerusalem: Van Leer Jerusalem Foundation, 1976), 14–15.

18. Alexander and Huggins, “On Changing the Way People See.”

19. Ibid.

20. The experiments with young children and with mentally retarded subjects are unpublished.

21. Nelson Zink and Stephen Parks independently discovered the same phenomenon. They found that a small light hung in front of a person’s eyes focuses the vision so narrowly that peripheral vision broadens, deepens, and forces the view to focus on the whole. See Zink and Parks, “Nightwalking: Exploring the Dark with Peripheral Vision,” WHOLE EARTH REVIEW (Fall 1991): 4–9.

22. Hubert Benoit, LET GO (New York: Samuel Weiser, 1973), originally published in French as LACHER PRISE (Paris: Le Courrier du Livre, 1958).

APPENDIX 4

SUPPLEMENT TO CHAPTERS 4 AND 11

A NEW TYPE OF MATHEMATICAL FIELD REQUIRED TO REPRESENT LIVING STRUCTURE AND THE BOOTSTRAP FIELD OF CENTERS

The picture of awakening space presented in chapter II requires a new mathematical view of space. It may be stated simply. We are considering a center as a geometric field-like phenomenon in space. In this sense, a center is a purely geometric thing, something which depends only on the arrangement, in space, of other centers. What we call its "life" is a geometric, structural feature which is a measure of the intensity of this field.

The suggestion is that a center is a pinpoint of actual life, a center of life, in the everyday and ordinary sense, which simply appears in space. Thus the geometric center which we first learn to see as a purely geometric thing is also a center of real life. The life emerges from matter through the organization of matter itself. All this arises from the pure recursive structure of the field of centers.

In order to describe this idea in consistent mathematical and physical terms, we have to make an important adjustment in our picture of physical reality. Most of us alive today have grown up with a certain view of physical reality—essentially the one created by physics. This view, which describes the matter in the universe in terms of a small number of interacting fields—gravitational and quantum mechanical—has been triumphantly successful in describing our physical universe, both at microscopic and at macroscopic levels.

Nevertheless, the mathematical picture of space as it must be, in order to account for the phenomena I have been describing in this book, requires a picture of space and matter which has an additional feature — only hinted at in mathematical physics so far.

In chapter 4 I showed, for a column, how each center helps to strengthen the others, and

how the whole column may be seen as a cooperating "field" of centers. In later chapters, we have seen more complex examples of a system of centers—like Paris in the neighborhood of the Seine—which pile function on function, and have seen how this system then performs deeply, in a functional way.

But it may not yet be clear how profoundly this idea shakes our current physics. The extraordinary thing does not lie in the "system" of these centers, nor in the fact that they cooperate to form a system. It is part of our general understanding of the world that systems cooperate to form more complex systems with new properties: that kind of thing is common in our present understanding of physics, biology, chemistry.

What is extraordinary here is something else. I have described the fact that each center has a certain life or intensity. By itself the original column has a rather low level of intensity. I have explained that, when the space between neighboring columns itself also forms a strong center, then the column "gets better." This means that the intensity or life of the center defined by the column becomes bigger at the moment when the center next to it—the void between the columns—appears on the scene. Similarly, when the capital appears on the scene—another center enters the field—then the center formed by the column itself and the center formed in the space between the columns both jump up in intensity again. And of course the center formed by the capital itself is also now more intense—because of the presence of these other two centers—than it would have been alone. And then, as we add the molding to the capital, once again the levels or intensities of all the other centers jump up again.

This is the thing which is peculiar. It is a type

of behavior which is not typical of Newtonian space at all. Indeed, it is a type of behavior which is also not typical of relativistic space, nor even of quantum mechanical space.

In our present view of physics, and of the physical universe, we often have systems made up of elements. It is commonplace that a system as a whole has properties which are caused by cooperation of elements. It is also commonplace that the behavior of the system as a whole may therefore be new or unexpected. In mathematical terms, this means that the measure or function which describes the whole system's behavior is often different from simple arithmetic combinations of the measures associated with the individual elements. It may be a very complex function of the measures associated with the elements. However, the measures associated with the individual elements do not themselves change as a result of the presence of these elements in the larger system.²³

This is typical of the mechanistic picture of the universe. When we make a clock, the various parts of a clock are, in their basic properties, unchanged by their presence in the clock. In the mechanistic view of things, the cooperation of different elements can produce new measures in the whole. However, the individual measures of the individual elements are always defined locally, not globally, and remain unchanged as the elements enter into combinations.

But what I have just said about the centers in a field of centers is quite different. The life of any given center depends on the whole field of centers in which this center exists. This means that the most fundamental property of each center—its degree of life—is defined not by the center itself but by its position in the entire field of centers.

This idea is reminiscent of Mach's principle—the idea that the behavior of any one particle is affected by the whole universe. In fact, the general idea that the life of each center in the universe is, somehow, dependent on the life of other centers might even be viewed as a generalization of Mach's principle.²⁴ It says that, as far as centers are concerned, the most fundamental property of each individual center (its intensity or life or centeredness) is affected by its position vis-à-vis all the other centers. Thus the intensity of a center can never be understood as a local property of that center itself, merely in terms of its own local structure. It is always a global property. It is affected by everything else. It cannot be measured by itself, since it depends entirely on its position in the whole. This idea requires an entirely different view of the physical substance we call space or matter.

This is the essence of the recursive definition of a center, which I have already laid out in chapter 4. But what I have not made clear before is that we do not currently possess any convenient mathematical representation of such a recursive field.

When I say that the conception of this recursive field lies outside our present conception of space and matter, what I mean is that we currently have no mathematical conception of any field in physics which has the recursive property defined in chapter 4 or chapter 11.

The classical fields have a field strength which is always dependent on something else, outside the field, and which produces the field. For example, the gravitational field takes values throughout space. These values are given as functions of the distribution of matter throughout space. It is true that the distribution of gravity will make the matter redistribute itself, and thus cause changes in the field, through time. But the gravity is not a function of the force of gravity itself. The electromagnetic field has two fields—an electric field and a magnetic field; each one is dependent on the rate of change of the other. Again, the system interacts with itself, in a way that causes very important effects. But the value of the magnetic field is not a function of the value of the magnetic field itself at other locations. Each of these fields is dependent on something else outside itself (the magnetic field is a function of the rate of change of the electric field, for instance), and can be calculated from knowledge of this something else.

But the intensities which occur in the field of centers, as I have described them in chapter 11, depend on the field's own values. The field apparently has the property that the field strength, at a given point, is a function of the many field strengths distributed through space in its vicinity. The field strength is a function of the other field strengths themselves. So, the field is self-dependent somehow.

There is no field of classical physics which is self-dependent in this fashion. I have not yet been successful in my own attempts to create a mathematical model of such a self-dependent field. I am fairly sure that the field must be some kind of hierarchical structure, in which different field strengths are nested inside each other. I would also guess that the field strength is strongly associated with the local symmetries described in chapters 4 and 11. But so far, I have been unable to construct a field with the necessary properties.

At each stage in our understanding of the physical world, we have always assumed that space has a certain mathematical structure. It is this mathematical structure of space which gives the world the properties we know. In particular, the mathematical description of space that is currently popular assumes that causal effects are local. This is a result of the neutral geometrical structure of the mathematics which we use to describe space.²⁵ It is precisely this assumption about space which is being challenged by the idea of the field of centers. In order to see space in a way which allows the field of centers to work in the way that I have been describing in this book, we need a different model: space itself must have a different mathematical structure.

We want to associate, with each point of space, a measure. I will call this measure "the intensity of the field" at that point. The intensity of the field measures how strong a center we have, how much life the field has at any given point.

If the field behaves in the way that we have seen empirically in many examples, and in the way that I have described for the example of the

column, we need a type of field which has the following property: as we increase the intensity of the field at certain points, the intensity of the field also increases at other points. In fact, the intensity at each point is a function of the intensities of the other nearby points. We may visualize this easily if we imagine a light bulb at each point in space. The intensity of the field at that point is given by the brightness with which the light bulb at that point glows. Somehow the light bulbs are linked. And we want a type of linkage which has the property that, when we make some bulbs glow more brightly, or screw in a new light bulb in a certain place, this also then makes certain other light bulbs in the system glow more brightly.

The idea that space is a kind of substance in which centers and their life depend on the configuration of centers as a whole, or even on some non-local extended field, holds extraordinary promise. It implies that the world is unpredictable in an entirely new kind of way—because the field of centers can produce levels of life, in the individual centers, that are not understandable from their local structure. In particular, it even contains a possible answer to the question "what is life," meaning "what is the quality, not the mechanism, of life?"—a mysterious question which has not yet been answered in three hundred years of mechanistic physics and biology. Every living system is a field of centers. Within the view that I have just explained, it becomes possible to imagine that certain configurations of centers have such organizing force that they create entirely new levels of intensity within the centers themselves—and therefore utterly transmute the material character of space itself.²⁶

Thus the bootstrap effect—the way that centers affect one another, and mutually intensify each other, conceived as a basic property of space and matter—may give us a coherent understanding of the way that life, a new and non-mechanical phenomenon, can be created within the so-called dead matter. But all this can only be understood within a framework where we recognize that matter itself—space itself—is a different sort of substance from the one which

we have understood before, because it allows the presence of a recursive field to occur.

What all this boils down to is that we may have to modify our picture of the world in a very fundamental way indeed. For more than a hundred years, we have conceived the matter in the universe as made of particles, floating and moving around in space. In recent years, it has become clear that the space itself also has a fine structure (something like a foam of bubbles, even in the so-called vacuum) and that the space where matter appears is only slightly different from the space where there is a vacuum. Thus we have been moving toward a picture of the universe as made of a kind of space, and where "ripples" occur in this space, what we call matter appears.

But the new picture which I propose here would make matter itself more dynamic than we have assumed so far. Up until now, we have treated the "ripples," which appear in this space, as essentially fixed in their nature. The elementary particles, for example—atoms, electrons, whatever—have always been assumed to have a more or less unchanging character, as they enter into combinations, and we have so far tended to think of matter as a kind of pattern of arrangements of elementary particles, which themselves then appear more or less unchanged in the combinations they create.

In the view that I am putting forward here, this would not necessarily be true. The centers that appear in space might be different, according to the context in which they appear, and might become more and more powerful, according to that context. Of course, it has always been known that an electron in an atom is not quite the same as a free electron, and that an atom in a molecule is not quite the same as an atom by itself—but we have assumed that

this kind of difference is minor and still easy to explain within the framework of thought that treats combinations as arrangements of the elementary particles.

The nature of a center and of the field of centers—if they have the character of the recursive field I have suggested—would indicate that space and matter have a more mysterious, more open-ended nature. It would appear that the space/matter itself can actually change—I mean by this that the space really somehow changes fundamentally in its local nature—as it becomes progressively more organized. All space has the capacity to have centers in it. When a center appears there, other centers are intensified by the presence of this center. The overall configuration of centers affects the space itself. Since each center intensifies others, we have a substance (the space/matter) which apparently has the capacity to generate life within itself almost spontaneously, since the production of order at any one point (a center) can increase the overall orderliness, and intensify the order which appears in other centers.

This view is consistent with the non-local interpretation of quantum mechanics, which holds that the behavior and character of one particle may be affected by structure in other regions of the universe, even by those regions which cannot have any causal or mechanical interaction with it.[27]

Where a center is formed, the space itself gradually comes to life. What we know as life is the condition which occurs as this precious life—or centeredness—is geometrically induced in space in the recursive way I have described; that is, from a mathematical point of view, what we would have to understand from the "awakening" of space.

NOTES

23. See, for example, the picture of field equations given in Erwin Schroedinger, SPACE TIME STRUCTURE (Cambridge: Cambridge University Press, 1960), throughout, or Charles Misner, Kip Thorne, and John

Archibald Wheeler, GRAVITATION (San Francisco: W. H. Freeman, 1973), chapters 1, 3, 4, 10-11, 20, 22-26.

24. Ernst Mach, SPACE AND GEOMETRY (La Salle, Illinois: Open Court Publishing Company, 1960). For dis

cussion of Mach's principle, see Thorne, Misner, Wheeler, GRAVITATION, section 21.12, 543-49.

25. The uniform spatial scheme of analytic or coordinate geometry, which has made us think of space as a neutral, lifeless, and dead substance, is due to Descartes. He first described this scheme in his GEOMETRY, vol. 6 of OEUVRES DE DESCARTES, which may be read in the uniform edition by Charles Adam and Paul Tannery (Paris, 1897-1913).

26. Again, see Mach, SPACE AND GEOMETRY. The same idea was also discussed in general philosophical terms, in Alfred North Whitehead, PROCESS AND REALITY. The more specific idea that the existence of life in the universe causes deep changes at the quantum mechanical level, and thus happens with changes in the actual structure of space and matter, has recently been discussed by a number of writers, including Roger Penrose, THE EMPEROR'S NEW MIND (Oxford: Oxford University Press, 1990), and Howard Pattee, "Biology and Quantum Physics," in TOWARDS A THEORETICAL BIOLOGY: I. PROLEGOMENA, C. H. Waddington, ed. (Chicago: Aldine Publishing, 1970).

27. For example, the experiments of J. Clauser, reported in S. Freedman and J. Clauser, PHYS. REV. LETT. 1972, 28, 934-41, and the experiments of Alain Aspect reported in Alain Aspect, P. Grangier and G. Roger, PHYS. REV. LETT. 1981, 47, 460-66; which indicate the existence of non-causal connections between phenomena too far apart to allow speed-of-light causal interactions to pass between them.

APPENDIX 5

A FURTHER SUPPLEMENT TO CHAPTER 3

BEHAVIOR OF AN ELECTRON AS A FUNCTION OF THE WHOLENESS

The fact that the behavior of the world depends on the wholeness which exists in space is not peculiar to buildings or to works of art. It is something fundamental about the world which controls even the behavior of subatomic particles. Recent discoveries in physics have shown that the behavior of matter at the subatomic level is modified — perhaps entirely governed — by the wholeness.

The problem is crystallized in the famous two-slit experiment. In this experiment, a hot wire sends off electrons, and these electrons are made to pass through two parallel slits and then hit a wall. You can see the experimental arrangement in the diagram below.

In order to understand the following discussion, you have to understand that each electron is a little stationary wave (almost like a turbulent tiny whirlpool) which flies like a bullet through the air. In the illustration on this page, bottom right, which is hugely enlarged, you can see little bright spots. Each bright spot marks the spot where one electron has hit the wall (a photographic emulsion). They are the bullet marks.

In addition, you have to understand that the hot wire can be controlled, so these bullets go intermittently, one at a time. So the stream of electrons is not a big stream where they all interact with each other, but a very slow stream, a radically slowed-down process, where one electron at a time comes off the hot wire, goes through the slits, and hits the wall.

Now consider the mysterious and wonderful behavior of these electrons. When just one slit

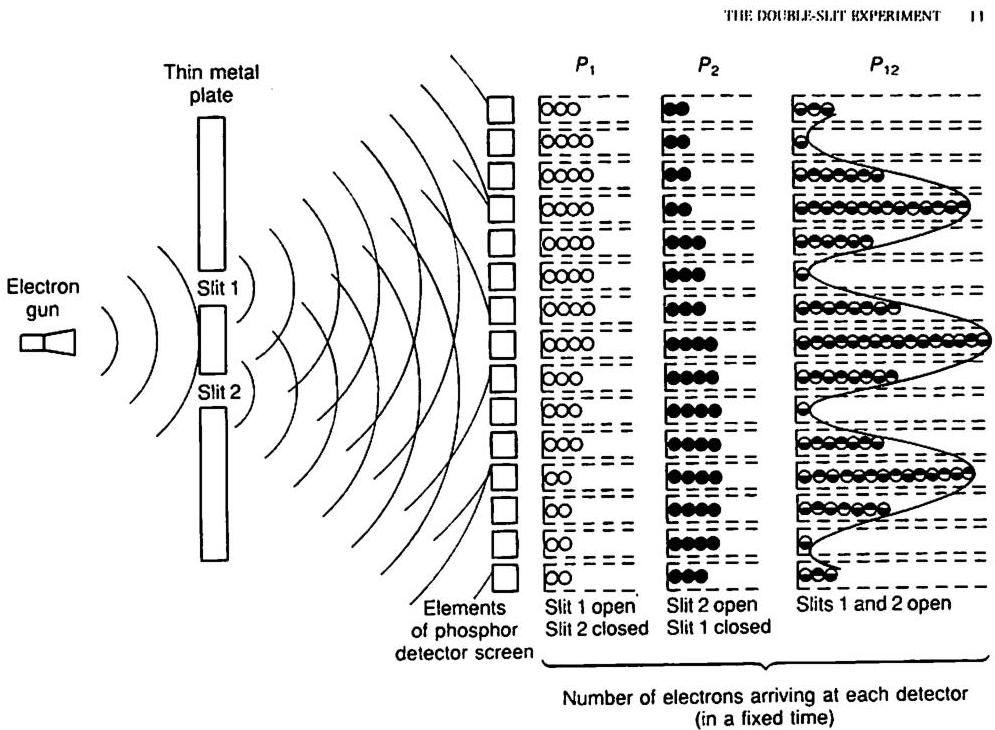
THE DOUBLE-SLIT EXPERIMENT 11

is open, the electrons that go through the slit make a smudged overall pattern on the wall. It is the same kind of pattern you would get from a spraying paint through the slit: thick in the middle and falling off towards the edges. The electron hits are most dense at the point closest to the slit where the electron's path would be a straight line, less dense at points on the wall further from the slit, and falling off smoothly as they get still further away. In effect the bullet-hits on the wall make a normal distribution on the wall. You can see this normal distribution in the diagram on the previous page. Column $\mathbf{P}_1$ shows what happens when slit 1 is open (by itself). Column $\mathbf{P}_2$ shows what happens when slit 2 is open (by itself). All this is rather straightforward.

What happens when both slits are open at the same time is dramatically different and not straightforward at all. The pattern made by the electrons hitting the wall now becomes an alternating pattern of dark and light bands, where virtually all the electrons have gone to the light bands, and almost none to the dark bands in between. This pattern is shown in the photographs on this page, and in column $\mathbf{P}_{12}$ of the diagram on the previous page.

A similar pattern is familiar in the case of light. The interference of light waves, to form interference fringes, as they are called, was discovered two hundreds years ago, by the French physicist Augustin-Jean Fresnel. Mathematically, it is explained by the fact that the wave fronts go through both slits, and then, as they hit the wall, cancel, or do not cancel, and thus form light and dark zones. For the electron, there is also a wave-like explanation, which is similar to the case of light, and whose mathematics explains this phenomenon perfectly. This is the famous wave equation of quantum mechanics. So, on a mathematical level, the two-slit experiment is worked out, and perfectly understood.

But really understanding what is happening is quite another matter. The problem is that the electrons, though wave-like in certain respects, really are like little bullets. You can see their bulletlike character in the bright spots on the photographic emulsion in my photographs. In the case of waves, the explanation of the fringes works because the waves coming from the light source go through both slits and then interfere as they

come together. But a particular electron, one electron, is like a little bullet. It cannot go through both slits. It only goes through one slit. It either goes through slit 1 or through slit 2. When we take this into account, and try to understand how the pattern of dark bands and light bands is built up, this is where the mysterious puzzle comes in.

Remember, the electrons are coming slowly, one at a time, to build up the pattern on the photographic emulsion. Let us imagine the case where only slit 1 is open. Slit 2 is closed. Look at the place on the wall which corresponds to a spot marked by my black arrow (diagram on page 463). In column P₁ we see four white balls there: meaning, in that zone there are four hits. This is one of the relatively dense spots in the normal curve. Quite a few electrons are going through slit 1 and landing in that spot.

Now look what happens when I open slit 2 (column P₁₂). Suddenly, this spot turns into one of the blank places on the wall. Electrons are now no longer hitting this part of the wall (where my arrow is). The remarkable part is that this is affecting all the electrons. If it were somehow affecting electrons going through slit 2, that would not be so mysterious. But this, the opening of slit 2 is affecting electrons which are passing through slit 1. Even those electrons which were formerly going through slit 1, and hitting the part of the wall where my arrow is, are now suddenly no longer doing it. Now they are moving so that they only hit the wall where the bright lines are, not where the blank, dark, shadows are.

Thus the opening of slit 2 is changing the mechanical behavior of the way an electron flies through slit 1. Yet that very same electron has no physical interaction with slit 2, nor with any other electron (remember they are coming one at a time). How is it possible for the opening of slit 2 to affect the motion of the electron that flies through slit 1?

It is this experiment which caused a revolution in physics, and underlies the importance of quantum mechanics. What kind of physical action is at work here? What is the physical, mechanical explanation of this extraordinary phenomenon? For seventy years now, physicists have been trying to understand it.

The problem, for a physicist, is the following. According to the normal assumptions of modern physics, a particle of matter can only be moved by collision with another bit of matter, or by a force: electromagnetic, gravitational, strong force, or weak force.

Yet in this experiment, we have a situation where the electrons going through slit 1 are moved (their motion is modified) by opening slit 2. As I have said, the mathematics is perfectly and beautifully worked out. Quantum mechanics, the name we give to that mathematics, can perfectly predict this phenomenon, in all its details. But what is the meaning? What is going on? What force is making the electron move like this?²⁸

Richard Feynman's explanation is charming: the mathematics works, but you cannot understand it. In his own words: "My physics students don't understand it either. That is because I don't understand it. Nobody does . . . The theory of quantum electrodynamics describes Nature as absurd from the point of view of common sense. And it agrees fully with experiment. So I hope you can accept Nature as she is — absurd. In short, there is no way to visualize what is going on. The theory of quantum mechanics explains it perfectly, to unbelievable mathematical accuracy. And that is all you need to know."²⁹

Other physicists have been less ready to accept the fact that the mathematics works, without an explanation. Einstein himself was uncomfortable with this kind of explanation and, up until the end of his life, considered quantum mechanics flawed because of it. And many other physicists, less matter-of-fact than Feynman, have also tried to find an "interpretation" which lets us see what is going on. Not a year goes by without some further attempt to explain it. This problem has been a subject of ongoing debate since about 1930, with no clearly agreed-on end in sight, even though the mathematics itself is perfectly understood — and is, in cases like the experiment here, able to predict what happens

to a level of accuracy hardly ever before attained in physics. The variety of attempted explanations is large, and includes some of the most far-fetched explanations ever given in the history of physics. Ideas that have been tried include the idea that the electron is not really there and is merely a wave of probabilities until it is observed; the idea that the universe is splitting constantly into billions of alternative and parallel universes. These apparently crazy ideas are not science fiction. They are sober proposals, well known in the physics literature.[30] They have been introduced because, within the normal assumptions of phys-

ics, opening slit 2 just cannot have a direct mechanical effect on the movement of an electron going through slit 1—so no one can make any intuitive sense of the electron and its behavior, and what it is that makes it move this way.

But there is a straightforward way of understanding all this, without involving such strange assumptions. We may assume that the electron's behavior is directly influenced by the wholeness of the experimental configuration. To make this explanation work, we must assume that the electron "wants" to go in harmony with the wholeness. That is, the electron somehow sees the wholeness as a real structure and behaves accordingly.

Some physicists are slowly coming to the conclusion that this—unexpected as it is—must be what is happening. Even the founder of quantum mechanics, Niels Bohr, foresaw it clearly. Bohr emphasized over and over again that we must learn to understand that "it is the whole experimental setup as one undivided system which is the key to the behavior of the particles."31 But during most of the past century, the idea that a large-scale geometrical configuration alone could affect the behavior of the electron has been too hard to swallow—because it is too much at odds with the assumption that only collisions and forces can make things move. We see this in Bohr's own writing: "it is only the circumstance that we are presented with a choice of either tracing the path of a particle or observing interference effects, that allows us to

escape from the paradoxical necessity of concluding that the behavior of an electron should depend on the presence of a slit through which it could be proved that it did not pass."32 In other words, the whole paraphernalia of modern physics (complementarity, uncertainty, etc.) are all elaborate circumlocutions in effect designed precisely to avoid the interpretation that the electron is affected by the wholeness, because physics has had no way of expressing this idea. In addition, no one has really known how to make any precise sense out of the idea of "the whole." We need to learn to see the wholeness of a given region of space as a precisely specified structure.

Once we look at wholeness as a real structure, we can make precise attempts to show how the different behaviors of the electron actually correlate with differences in the structure of the wholeness. Look at the two experimental configurations in the two-slit experiment. In one case, we have a system of centers which is asymmetrical and flattened out. It is not hard to see that this system of centers might create the smudged-out distribution of hits on the wall. In the other case, we have a symmetrical system in which two similar systems of centers overlap in a way very similar to the overlap in the ripples going out from two pebbles thrown into a pond. It is not hard to imagine this system of centers guiding the electrons to create the interference fringes on the wall. And indeed, one possible explanation along these lines has been worked out by David Bohm's coworkers.33 On this page, I show the quantum potential, worked out by Bohm and his coworkers, to show a geometric explanation of the way the wholeness of the space itself can explain the mathematical results of quantum mechanics. In 1988, Bohm told me in conversation that in his mind the wholeness defined in Book 1, is essentially the same structure as that which he calls the "implicate order," and considers responsible for the motion of the electrons.34,35

Full acceptance of this idea, if it is one day accepted, will cause a revolution in physics. The idea that the wholeness might actually be powerful enough to cause a change in the motion of

an electron, would greatly change our idea of how matter behaves. And the mental context of this confirmation would then make the role of the wholeness as the underpinning of all architecture, much easier to grasp.36

Whether Bohm's particular version ultimately turns out to be true or not, the main point still remains. The experiments of 20th-century physics have shown conclusively that the electron is guided by the wholeness in which it moves. This is what a sober appraisal of the two-slit experiment does lead to. Indeed, whether we accept it explicitly or not, that is what quantum mechanics does anyway. Quantum mechanics asserts, via the mathematics, that particles are physically affected in their behavior by the wholeness of the space in which they move.

In the words of Vigier et al.: "The interpretations of Bohr and of de Broglie-Bohm-Vigier both emphasize that the fundamentally new feature exhibited by quantum phenomena is a kind of wholeness completely foreign to the post-Aristotelian reductionist mechanism in which all of nature in the final analysis consists simply of separate and independently existing parts whose motions, determined by a few fundamental forces of interaction, are sufficient to account for all phenomena."37

It might be said that this is the most important discovery of modern physics. Subatomic particles cannot be viewed as isolated elements which only interact mechanically with other elements through the medium of forces and collisions. Both their existence and their behavior are controlled by their relation to the wholeness of the world around them. It is the wholeness — either in the particular sense which I have defined, or in some other very similar sense — which is the governing structure of reality.

If true, this implies that the general view I have presented throughout Book 1—with its emphasis on the functional importance of the wholeness—is not restricted to buildings or works of art, but is valid and essential even in those parts of the world we have historically believed to be mechanical in nature.

NOTES

28. David Bohm, QUANTUM THEORY (Englewood Cliffs, N.J.: Prentice Hall, 1951), especially chapter 8, "An Attempt to Build a Physical Picture of the Quantum Nature of Matter," 144–72.

29. Richard Feynman, QUANTUM ELECTRODYNAMICS (Princeton, N.J.: Princeton University Press, 1985), 9–10.

30. The most peculiar interpretations have been well summarized in Nick Herbert, QUANTUM REALITY.

31. Niels Bohr, "Discussion with Einstein on Epistemological Problems of Atomic Physics," first published 1924, reprinted in Wheeler and Zurek, eds., QUANTUM THEORY AND MEASUREMENT (Princeton, N.J.: Princeton University Press, 1983), 30.

32. Ibid., p. 24.

33. J. P. Vigier, C. Dewdney, P. R. Holland and A. Kyprianidis, "Causal Particle Trajectories and the Interpretation of Quantum Mechanics," in B. J. Hiley and F. J. Peat, eds., QUANTUM IMPLICATIONS (London, 1987), 169–204.

34. Taped public dialogues, Krishnamurti Center, Ojai, California, 1988.

35. See David Bohm, WHOLENESS AND THE IMPLICATE ORDER (London: Routledge Kegan Paul, 1980).

36. In recent years the theory of quantum mechanics based on wholeness, has been accepted by physicists as the most economical and most accurate way of understanding the motion of electrons. The sense of mystery and ambiguity that used to surround quantum mechanics (in its Copenhagen form) has almost disappeared, and given way to a view that this is the most practical and commonsense way to deal with the physics. For a standard exposition see Peter Holland, THE QUANTUM THEORY OF MOTION: AN ACCOUNT OF THE DE BROGLIE-BOHM CAUSAL INTERPRETATION OF QUANTUM MECHANICS (Cambridge: Cambridge University Press, 1993).

37. P. Vigier, C. Dewdney, P. R. Holland and A. Kyprianidis, "Causal Particle Trajectories," 201.

APPENDIX 6

SUPPLEMENT TO CHAPTERS 4 AND 5

CALCULATING DEGREE OF LIFE IN DIFFERENT FAMOUS BUILDINGS: A FIRST APPROXIMATION TO A FULLER MATHEMATICAL TREATMENT

In chapters 4 and 7, and again in the conclusion, I have repeatedly referred to the fact that life, as I have defined it, is mathematical. By this I mean that it arises because of the mathematics of space itself. Since living centers arise primarily as symmetries and structures of symmetries, their presence and their density can, in principle, be calculated for any given configuration. That means, then, that the life is, in principle, a computable property, which arises in space as a result of the configuration of the space. Some of the conceptions presented in appendixes 1, 2, and 4 begin to show how this may be made precise.³⁸ And in chapter 5, pages 188-192, I have given a detailed treatment of thirty-five black and white patterns, showing how the rank order of “coherence” (an early experimental form of what I have called life throughout this book) for the thirty-five patterns is predicted almost exactly by counting the LOCAL SYMMETRIES that appear nested throughout the structure at all its levels taken together.³⁹

In spite of these explicit successes, I believe we are still rather far away from the possibility of making useful large-scale calculations in buildings. This is because the mathematical problems described in appendices 2 and 4 are difficult, and will, I am sure, remain inaccessible to a full treatment for some time to come.

However, a recent study which presents a first rough approximation shows strong results, albeit with crude means. I believe it is important to show this result simply to underline the fact that living structure is, in principle, susceptible to mathematical treatment, and may therefore be regarded as a part of physics.

In 1997, Nikos Salingaros, professor of mathematics at the University of Texas, constructed a first approximation for a measure of life, $L$, derived largely from the theory in this book, and showed how to apply it to make approximate calculations of degree of life for a variety of buildings. In a paper published as “Life and Complexity in Architecture from a Thermodynamic Analogy,” he has shown that this measure $L$ gives a preliminary approximation for twenty-four well-known buildings, ranging from ancient to modern, including the Parthenon, the Pompidou Centre, Salisbury Cathedral, the TWA terminal at JFK airport in New York, the Sydney Opera House, Hagia Sophia, the Alhambra, the Maison Horta in Brussels, the chapel at Ronchamp, and the Norman Foster bank in Hong Kong.⁴⁰

Roughly we may consider Salingaros’s measure $L$ in the following way. The measure $L$ which I have put forward in appendix 2 counts living centers by counting locally symmetric sets.⁴¹ That is possible in a very small structure (like the black and white strips I used), harder in a larger structure. It also makes no explicit use of the additional recursive information inherent in the other fourteen properties.

Salingaros has composed a measure which can be applied to a relatively large configuration, not by actually counting living centers, but by estimating them statistically. This allows his measure to be applied to large and complex structures.

His measure is based on two component measures that he calls $H$ and $T$: $H$, what he calls harmony, estimates the number of LOCAL SYMMETRIES present in a configuration by assigning scores to five different features of the symmetries. $H$ is therefore somewhat similar to the use of local symmetries as the primary component in the measure, but is used so that one does not have actually to count thousands of symmetries, but instead estimates, by inspection, the overall density of local symmetries.

$T_{*}$ which Salingaros calls temperature, estimates LEVELS OF SCALE, CONTRAST, BOUNDARIES, and perhaps also STRONG CENTERS—once again, in a broad-brush approach which does not attempt to count individually the strong living centers, but rather estimates the density of occurrence of these properties.

By multiplying $T$ and $H$ to get $L$, Salingaros's $L$ then gives a very rough measure of local symmetries, strong centers, levels of scale, boundaries, and contrast in the configuration.

In his paper he provides the rules by which he obtained the estimates needed to calculate $T$ and $H$ for the different buildings. Each of these two measures is the sum of five parameters, each able to take only three values, 0, 1, or 2 (missing, partly present, or strongly present), which are to be estimated by the observer. This makes measurement easy to do, and reasonably objective.

The following table gives values of $H$, $T$, and $L$ for twenty-four important buildings, derived by measurement according to Salingaros's procedure. They appear here just as published in his paper.

| DEGREE OF LIFE IN

TWENTY-FOUR FAMOUS BUILDINGS
LISTED IN ORDER OF DECREASING L
THE LIFE, L, IS DEFINED BY L = TH
DATE	BUILDING	PLACE	ARCHITECT	T	H	L
14th c.	ALHAMBRA	Granada	unknown	10	9	90
17th c.	TAJ MAHAL	Agra	unknown	10	9	90
7th c.	DOME OF THE ROCK	Jerusalem	unknown	9	9	81
6th c.	HAGIA SOPHIA	Istanbul	Isidoros, geometer	10	8	80
13th c.	KONORAK TEMPLE	Orissa	unknown	8	8	64
9th c.	PALATINE CHAPEL	Aachen	Odo of Metz, builder	7	9	63
11th c.	PHOENIX HALL	Kyoto	unknown	7	9	63
13th c.	CATHEDRAL	Salisbury	unknown	7	9	63
c. 1700	GRANDE PLACE	Brussels	unknown	9	7	63
16/17th c.	ST. PETER'S	Rome	Bernini	10	6	60
5th c. BC	PARTHENON	Athens	Iktinos, builder	7	8	56
12/14th c.	BAPTISTERY	Pisa	Salvi, builder	7	8	56
1898	MAISON HORTA	Brussels	Horta	8	7	56
1906	CASA BATLO	Barcelona	Gaudi	8	5	40
1954	WATTS TOWERS	Watts	Rodia	10	4	40
1974	MEDICAL FACULTY HOUSING	Brussels	Kroll	7	4	28
1977	POMPIDOU CENTRE	Paris	Piano	6	4	24
1986	BANK	Hong Kong	Foster	3	7	21
1936	FALLING WATER	Bear Run	Wright	4	5	20
1973	OPERA HOUSE	Sydney	Utzon	4	5	20
1958	SEAGRAM BUILDING	New York	Mies van der Rohe	1	8	8
1961	TWA TERMINAL	New York	Saarinen	3	2	6
1965	SALK INSTITUTE	La Jolla	Kahn	1	6	6
1955	CHAPEL	Ronchamp	Le Corbusier	1	2	2

I find these preliminary experimental results highly instructive. The Alhambra and the Taj Mahal have a very high score, 90, Hagia Sophia 80, Salisbury Cathedral 63. At the low end, the TWA terminal has a very low score of 6, Wright's Falling Water has 20, the Seagram building 8, and the Sydney Opera House 20. At an intermediate level, Watts Towers has 40, Gaudi's Casa Batló has 40, and Sullivan's Carson Pirie Scott building has 56.

You may say these numbers are childish, since of course the assignment of numbers is mechanical, and hardly commensurate with the subtlety of the question. And, indeed, there are odd points, if we compare them with the judgement that would be reached by applying the criterion of life (as in chapters 1 or 2, or 10), or indeed commonly accepted judgement by architects or others. The Taj Mahal, at 90, is too high; the Parthenon, at 56, too low. Le Corbusier's Ronchamp at 2, is somewhat too low. Yes, by all means, there are mistakes. The function does not work, perfectly, to predict degree of life. But it does work to an unexpected degree. The success of the experiment outweighs the mistakes.

It is telling that a simply constructed arithmetical function, based on the considerations of the nature of living structure, no matter how crudely, could get these kinds of results at all. It shows that, while the question itself may be a million times more subtle, there is something tangible, and ultimately measurable, in the degree of life the living structure has.

Of course, the specific measurements which Salingaros has reported in his table, are over-simplified, even for his own measure. These measurements are based on a single photograph of each building and deal, therefore, only with the organization of the facade. This is, certainly, only a start. Furthermore, the measurements of $T$ and $H$ are very sketchy, certainly not yet of the level of sophistication required by a detailed analysis of life. Nor does Salingaros's measure deal with the recursion inherent in the field of centers.

But still, when one considers the fact that there are so many "buts," and yet that the results are somewhat close to one's intuitive assessment of these buildings, one must marvel that in such a crude net he has caught so much.

It is a time-honored tradition in physics to make a rough calculation, to get quick and dirty results, merely to see if a given theory is correct, even to within an order of magnitude. That one can hardly doubt. To me, given the crudity of the measures $T, H$ , and $L$ , as defined, it is truly remarkable that they give results that are consistent with our feelings about life.

This does not mean that they represent the last word of what is possible. Of course they do not. Many of these results would need refinement in a more careful analysis. For example, Ronchamp does have a massive, dark, and brooding silence. Whatever life it has in its interior is not yet captured in Salingaros's measurement. That is to be expected, given that he examined only the exterior. But also the weight, the heaviness, the cool atmosphere of the chapel, these create a life which is more difficult to capture arithmetically. Depending as they do on ECHOES, POSITIVE SPACE and INNER CALM within the structure, they are properties that are not yet caught by this first version of Salingaros's $L$ .42

Bernini's St. Peter's is indicated to have more life than one would accord to it, intuitively. That is probably because the Salingaros measure is too greatly dependent on what he calls the temperature (the busy-ness of structure). A more sophisticated measure—a second draft of $L$ , perhaps—will have a way of recognizing mere busy-ness as noise, and will lower the $L$ accordingly.

A few architects tend to dismiss the findings of Salingaros's experiment on the grounds that he does not know enough about architecture. This, I believe, comes about because so many modern heroes of architecture fare so badly on this measure. Kahn's Salk Institute is second lowest on the list. Even those who are open-minded to the need for a new way of

thinking may not be ready to accept such drastic evaluations — and will therefore find refuge in the idea that Salingaros does not know enough. But here I think they are mistaken, and perhaps self-delusional. The Salk Institute and the Seagram Building may well be icons of the modernist movement. But according to the analysis of life which I have given, they must be discounted as having any particularly high degree of life.

In this respect, Salingaros’s measure picks up these difficulties with many modern buildings rather accurately, and forces us to examine, more carefully, which buildings are truly alive, and which are not. It might be said that just because Salingaros is ignorant of architectural fashion, his measure is therefore to be trusted more: it has no built-in prejudice. It comes only from the wish of a physicist, to find a measure that accords with experience as nearly as possible.

Degree of life, as measured by Salingaros’s $L$, corresponds reasonably to the experience of life in these buildings, as it might be measured, for instance, using the mirror-of-the-self test from chapter 10. The strength of this result is greatly encouraging. It may be considered even more encouraging when one recognizes that the arithmetical measure presented in Salingaros’s paper is an extremely rough first approximation. Yet it gets results that match and predict experience with surprising accuracy. It does manage, in approximate form, to estimate the extent of living structure in the buildings — that is, the degree to which living centers appear and support each other.

Professor Howard Davis (from the Department of Architecture, University of Oregon), after examining Salingaros’s result, has commented to me that he believes a sequence of

measures of this kind should be tested until one that is even stronger can be found. It is his view that plans and sections, not only elevations, should be tested. He points out, also, that much of the rank order that one feels among these buildings is explained by $H$ (the symmetries), and that the temperature $T$ is doing relatively less work than $H$ in predicting this rank order. $T$ is also creating the excessively high scores for St. Peter’s, for the Taj Mahal, and for the Foster bank, while giving scores that are too low for Ronchamp and the Parthenon.⁴³

After careful experimentation, I believe a measure of simplicity, coupled with levels of scale, which counts occurrences of THE VOID, INNER CALM, and gives more weight to LEVELS OF SCALE, ought to be incorporated, and would produce a measure that predicts life with a higher degree of accuracy.

In any case Salingaros’s work opens the door to a rich field of study. Measurements of degree of life in different buildings, as gauged by the observer’s felt wholeness or by the mirror-of-the-self test, coupled with efforts to build arithmetic functions of the fifteen properties in the buildings, should soon lead to more and more powerful measures.

All this measurement is possible because centers are formed from symmetries and differentiations, and these arise within the mathematics of a configuration, which can be computed. Thus life itself arises as a result of mathematical operations in the space. When in the future we make more subtle, more complex determinations of the space, its symmetries, its centers, and the recursion, we shall, I hope, get more subtle results still. We just need to work hard to decipher it.

But the relative degree of life is already there, in the computable, mathematical, structure of the space.

NOTES

38. See pages 446-8.
39. See pages 188-192.
40. Salingaros, “Life and Complexity in Architecture from a Thermodynamic Analogy,” op. cit., 165-73.
41. See page 450.
42. Salingaros has begun efforts to refine and extend his first draft measure, in a second-draft measure where he places more emphasis on levels of scale, and on nesting of centers. See Klinger and Salingaros, op. cit.
43. Personal communication, May 1998.

ACKNOWLEDGEMENTS AND PICTURE CREDITS

My nearly boundless gratitude for all the help I have received with the content, ideas, discussion, and production of these four books from many, many people during the last twenty four years is expressed, with love and deep personal emphasis, on the eight pages that appear at the end of Book Four.

In addition, in this book I gratefully acknowledge the use of pictures, photographs, and illustrations owned by the following persons and institutions. All illustrations not mentioned belong to or are the work of the author.

Preface

p. 9 © 1990, Amon Carter Museum, Fort Worth Texas, Bequest of Eliot Porter; p. 11 F.W. Funke; p. 12 left: Arthur Upham Pope, A Survey of Persian Art, Soroush Press, p. 419; p. 12 right: Kenzo Tange and Noburu Kawazoe, Prototype of Japanese Architecture, MIT Press, 1965, p. 130; p. 13 top left: Georg Kohlmaier and Barna von Sartory, Das Glashaus, Prestel Verlag, 1981, plate 612, p. 655; p. 13 top right: Georg Kohlmaier and Barna von Sartory, Das Glashaus, Prestel Verlag, 1981, plate 487, p. 543; p. 13 bottom: Yoshio Watanabe; p. 14 left: Leonardo Benevolo: The History of the City, MIT Press, 1980, fig. 1364; p. 14 top right: Thom Jestico; p. 14 center right: Lee Nichol; p. 14 bottom right: Hiroshi Misawa;

Chapter 1

p. 19 right: Artemis Verlag; p. 20 Paschall; p. 21 Jan Derwig; p. 31 K. Nakamura; p. 33 Ace; p. 34 © 1990, Amon Carter Museum, Fort Worth, Texas, Bequest of Eliot Porter; p. 35 © 1990, Amon Carter Museum, Fort Worth, Texas, Bequest of Eliot Porter; p. 36 Magnum Photos, Inc., © 1946 Henri Cartier Bresson; p. 37 bottom: Alfred Eisenstaedt/LIFE Magazine © Time, Inc.; p. 39 Henri Cartier-Bresson; p. 40 Hirmer Verlag; p. 41 Hans Jirgen Hansen; p. 42 Roland and Sabrina Michaud/Rapho; p. 43 top: Andre Martin; p. 43 bottom: Japan Folk Crafts Museum, Tokyo; p. 44 top left: Andre Martin; p. 44 bottom right: Staatliche Museum, Berlin-Preussischer Kulturbesitz. Museen & Islamische Kunst; p. 45 Roderick Cameron, Shadows from India, William Heinemann, Ltd., 1958, p. 73; p. 46 Carl Nordenfalk, Celtic and Anglo-Saxon Painting, George Braziller, 1977, plate 1, p. 33; p. 47 top: Soetsu Yanagi, The Unknown Craftsman, Kodansha; p. 47 bottom left: Inge Morath; p. 47 bottom right: © Smithsonian Institution, Freer Gallery of Art; p. 48 top left: Gunvor Ingetad Traetteberg, Folk Costumes of Norway, Dreyers Forlog, 1966, p. 28; p. 48 top right: José Ortiz Echage; p. 48 bottom: Roland Michaud/Rapho; p. 49 Ajit Mookerjee, Yantra Art, Kumar Gallery, 1966, plates 2-4; p. 50 Art Resource; p. 51 Alfred Eisenstaedt/LIFE Magazine © TIME, Inc.; p. 52 top left: Artemis Anninou; p. 52 top right: H.S.K. Yamaguchi; p. 52 bottom: Alfred Eisenstaedt/LIFE Magazine © TIME, Inc.; p. 53 top: Artemis Anninou; p. 53 bottom: Michel Hoog, Paul Gauguin: Life and Work, Rizzoli International Publications, 1987, p. 185, plate 128; p. 54 top: Hal Davis; p. 54 bottom left: Kaku Kurita/Gamma-Liaison; p. 54 bottom right: Jean Leymarie, Herbert Read, and William S. Lieberman, Henri Matisse, University of California Press, 1966, p. 112, plate 82; p. 55 top: Pedro Guedes, Encyclopedia of Architectural Technology, McGraw-Hill Book Co., 1979, p. 304; p. 55 bottom: Andreas Feininger; p. 56 Alfred Eisenstaedt/LIFE Magazine © TIME, Inc.; p. 57 The Metropolitan Museum of Art, Mr. and Mrs. Henry Ittleson, Jr., Fund, 1956 (56.13); p. 59 bottom: Elliot Kaufmann Photography; p. 61 Magnum Photos, Inc. © 1935 Henri Cartier-Bresson

Chapter 2

p. 64 left: Bruce Dale, © National Geographic Society; p. 64 right: Joseph Rodriguez, National Geographic Society Image Collection; p. 69 top left: Magnum Photos Inc. © 1959 Bruce Davidson; p. 69 top right: Vallhonrat; p. 70 bottom left: © Kevin Fleming; p. 70 bottom right: Joanna Pinneo; p. 71 left: Photo Stuart Franklin; p. 71 right: Photo Stuart Franklin; p. 73 right: Elliot Kaufmann Photography; p. 75 left: Carl Nordenfalk, Celtic and Anglo-Saxon Painting, George Braziller, 1977, plate 1, p. 33

Chapter 3

p. 88 Ullstein Bilderdienst; p. 91 Photo Emil Otto Hoppe, © 1994 The E.O. Hoppe Trust, All Rights Reserved; p. 93 Magnum Photos, Inc. © 1962 Henri Cartier-Bresson; p. 97 top: Jack D. Flam, Matisse on Art, E.P. Dutton, 1978, p. 118; p. 97 bottom: Jack D. Flam, Matisse on Art, E.P. Dutton, 1978, p. 136; p. 99 top: Tony Hey and Patrick Walters, The Quantum Universe, Cambridge University Press, 1987; p. 99 bottom left: Tony Hey and Patrick Walters, The Quantum Universe, Cambridge University Press, 1987, p. 10; p. 102 © Ken Heyman; p. 103 top: Magnum Photos, Inc. © Henri Cartier-Bresson; p. 103 bottom: Byzantine Institute; p. 104 top: © Ken Heyman; p. 104 bottom: Magnum Photos, Inc. © 1938 Henri Cartier-Bresson; p. 105 Manuel Alvarez/Bravo

Chapter 4

p. 117 top: Bob Gibbons; p. 117 bottom: Gareth Lovett Jones; p. 123 The British Architectural Library, Institute of British Architects; p. 126 left: Artemis Anninou; p. 126 right: Martin Hurlimann; p. 127 Georg Gerster; p. 133 right: Gwathmey Siegel and Associates, Photo David Hirsch; p. 135 top: Magnum Photos, Inc. © James Nachtwey

Chapter 5

p. 146 Marguerite Duthuit-Matisse and Claude Duthuit, Henri Matisse, Vol. II, Claude Duthuit, Paris, Cat. #464, plate 70; p. 147 top left: Record Houses 1987, Vol. 175, No. 5, April 1987, p. 156; p. 147 top right: William W. Owens, Jr.; p. 147 bottom left: Eugen Gomringer, Josef Albers, George Wittenborn, Inc., p. 151; p. 147 bottom right: Shinkenchiku-Sha, The Japan Architect Co., Ltd., Tokyo; p. 148 center: Neuberger Museum of Art, gift of Roy R. Neuberger. Photo by Jim Frank; p. 148 bottom: Charles K. Wilkinson, Iranian Ceramics, Asia House Gallery Publication, 1963, plate 16; p. 149 top: Hans C. Seherr-Thoss; p. 149 bottom: Steen Eiler Rasmussen; p. 150 Roderick Cameron, Shadows from India, William Heinemann Ltd., 1958, p. 45; p. 151 Andre Martin; p. 152 Courtesy Bruce Goff; p. 153 Otto E. Nelson; p. 154 top: Steen Eiler Rasmussen, *Towns and Buildings, Harvard University Press, 1951, p. 9; p. 154 bottom: Magnus Bartlett; p. 155 left: Michael J. Crosbie, 'Gentle Infill in a Genteel City', Architecture, New York, July 1985, p. 46; p. 156 bottom: Kurt Erdmann, The History of the Early Turkish Carpet, Oguz Press, 1977, color plate III; p. 157 top left: Edward Allen, AIA; p. 157 top right: J. David Bohl; p. 157 bottom left: Arthur Upham Pope, Masterpieces of Persian Art, The Dryden Press, 1945, plate 103; p. 158 Toni Schneiders, Lindau; p. 160 top left: Otto von Simpson, The Gothic Cathedral, Pantheon Books, 1965, plate 33; p. 160 top right: © Foto Mas, Barcelona; p. 160 bottom: Limousine City Guide, Airport Transport Service Co., Ltd., Tokyo, Winter 1983, Vol. 4, No. 1, Cover Photograph; p. 161 top: Gregory Battcock, 'Die Aesthetik des Televideos', Design ist Unsichtbar, Loecker Verlag, 1980, p. 363; p. 161 bottom: Gregory Battcock, 'Die Aesthetik des Televideos', Design ist Unsichtbar, Loecker Verlag, 1980, p. 363; p. 161 bottom: Gregory Battcock, 'Die Aesthetik des Televideos', Design ist Unsichtbar, Loecker Verlag, 1980, p. 363; p. 162 left: Bildarchiv, ONB, Vienna; p. 162 top right: Aris Konstantinidis; p. 162 bottom right: Edward Allen, AIA; p. 163 Roland Michaud/Rapho; p. 163 bottom left: Foto Mas, Barcelona; p. 163 bottom right: Yoshio Watanabe; p. 164 © Estate of Andre Kertesz; p. 165 The Textile Museum, Washington, D.C., No. OC1.77; p. 166 Norman Carver, Jr.; p. 167 top left: Andre Held; p. 167 top right: Ludwig Goldsheider, ed., Leonardo da Vinci, Phaidon Publishers (Phaidon Press Ltd.), 1951, plate 121; p. 167 center left: Yukio Futagawa; p. 167 center right: F. J. Christopher, Basketry, Dover Publications, Inc., 1952, Ill. 20; p. 167 bottom: Aris

Konstantinidis; p. 169 © 1990 Amon Carter Museum, Fort Worth Texas, Bequest of Eliot Porter; p. 170 top: Art Resource/Scala; p. 170 bottom: Fabio Galli; p. 171 Ishimoto Yasuhiro; p. 172 Christie's Images; p. 173 Nolli plan of Rome; p. 174 top: Soetsu Yanagi, The Unknown Craftsman, Kodansha; p. 175 top: Serare Yetkin, Turk Hali Sanati, Bankasi Kultur Yayinlari, 1974, color plate 1; p. 175 bottom: Staatliche Museen zu Berlin-Preussischer Kulturbesitz-Museum fr Islamische Kunst; p. 176 top: Private Collection; p. 176 middle: Werner Stuhler and Herbert Hagemann, Venetia, Universe Books, Inc., 1966, plate 23; p. 176 bottom: Arthur Upham Pope, A Survey of Persian Art, Vol. II, Soroush Press, p. 171, fig. F; p. 177 top left: Hisao Koyama; p. 177 top right: George Heinrich, 1999; p. 177 bottom: Yukio Futagawa; p. 178 left: Moshe Safdie and Associates; p. 178 right: Reha Gunay; p. 179 left: Yanni Petopoulos, Tulips, Arabesques and Turbans, Abbeville Press, Inc., 1982, p. 2; p. 179 right: Novosti Press Agency; p. 181 top left: Japan Folk Crafts Museum, Tokyo; p. 183 top: Novico; p. 183 bottom: Musée Historique des Tissus, Lyons, no. 35488 (972.IV.I); p. 184 top: Roar Hauglid, Norske Stavkirker, Dreyers Forlag, 1976, p. 173, fig. 143; p. 184 bottom: Arthur Upham Pope, Masterpieces of Persian Art, The Dryden Press, 1945, plate 27; p. 185 Yukio Futagawa; p. 186 top: M. Wenzel; p. 186 bottom: The Library of Congress; p. 187 Oleg Grabar, The Alhambra, Harvard University Press, 1978, overleaf; p. 188 Don Juan Antonio F. Oranzo; p. 192 Ab Pruis; p. 193 Francoise Henry, The Book of Kells, Alfred A. Knopf, 1974, plate 125; p. 194 Hans C. Seherr-Thoss; p. 195 left: Kiyosi Seike, The Art of Japanese Joinery, John Weatherhill, Inc., 1977, plate 1; p. 195 right: Roar Hauglid, Norske Stavkirker, Dreyers Forlag, 1976, plate 278; p. 196 top right: Hiroshi Morimoto; p. 196 bottom: David Sellin; p. 197 top: Seth Joel, Metropolitan Museum of Art; p. 197 bottom: Kiyosi Seike, The Art of Japanese Joinery, John Weatherhill, Inc., 1977, p. 80, fig. 51; p. 198 Roland Michaud/Rapho; p. 199 Art Resource; p. 200 Charles K. Wilkinson, Iranian Ceramics, Asia House/Distributed by Harry N. Abrams, Inc., 1963, plate 49; p. 201 top left: Elias Petropoulos; p. 201 top right: Hans C. Seherr-Thoss; p. 201 bottom: Smithsonian Institution, Freer Gallery of Art; p. 202 William F. Winter; p. 204 top: Evelyn Hofer; p. 204 bottom: Leonardo Benevolo, The History of the City, MIT Press, 1980, p. 314, fig. 497; p. 205 Scala/Art Resource; p. 206 top left: Elias Petropoulos; p. 206 top right: Bildarchiv Preu icher Kulturbesitz; p. 206 bottom left: Staatsbibliothek Berlin, Picture Archive; p. 206 bottom right: Ludwig Goldscheider, Leonardo da Vinci, The Phaidon Press, 1951, No. 40; p. 207 top: Ursula Pfistermeister, Artelshofen; p. 207 bottom: Steen Eiler Rasmussen, Experiencing Architecture, MIT Press, 1962, p. 140; p. 208 John van der Zee, The Gate, Simon and Schuster, 1931, endpaper.; p. 209 Werner Stuhler and Herbert Hagemann, Venetia, Universe Books, Inc., 1966, plate 56; p. 210 Smithsonian Institution, Freer Gallery of Art; p. 212 bottom: Andre Martin; p. 213 Otto E. Nelson; p. 214 top: Eugenio Battisti, Filippo Brunelleschi, The Complete Work, Rizzoli, 1981, p. 71; p. 214 bottom: Bernard Rudofsky; p. 217 top: Dr. Eva Frodl-Kraft; p. 217 bottom: Yukio Futagawa; p. 218 bottom: Otto E. Nelson; p. 219 top: Everest Films, Norman Dyhrenfurth; p. 219 bottom: Edward Allen, AIA; p. 220 top: Steen Eiler Rasmussen, Experiencing Architecture, MIT Press, 1962, p. 68; p. 220 bottom: Gunner Bugge and Christian Norberg-Schulz, Stax og Lajf I Norge (Early Wooden Architecture in Norway), Byggekunst, Norske Arkitekters Landsforbund, 1975, p. 122; p. 221 Gunner Bugge and Christian Norberg-Schulz, Stax og Lajf I Norge (Early Wooden Architecture in Norway), Byggekunst, Norske Arkitekters Landsforbund, 1975, p. 122; p. 223 bottom: Turizm Tanitma Bak; p. 224 top: Arthur Upham Pope, A Survey of Persian Art, Vol. IX, Soroush Press, p. 561; p. 224 bottom: Magnus Bartlett; p. 225 Rijksmuseum, Amsterdam; p. 226 left: F.W. Meader, Illustrated Guide to Shaker Furniture, Dover Publications, Inc., 1972, fig. 162, p. 82; p. 227 top: David Sellin; p. 227 bottom: Yukio Futagawa; p. 228 Janice S. Stewart, The Folk Arts of Norway, Dover Publications, Inc., 1972, p. 15, fig. 7; p. 229 Roderick Cameron; p. 230 F.W. Funke; p. 232 top: Bruckmann; p. 232 bottom: Hans Jurgen Hansen, Architecture in Wood, The Viking Press, Inc., 1971, p. 88; p. 233 Yukio Futagawa; p. 234 Norman Carver, Jr.; p. 235 Michel Hoog, Paul Gauguin, Life and Work, Rizzoli International Publications, Inc., 1987, p. 70, plate 40

Chapter 6

p. 247 A.R. von Hippel, MIT Historical Collection, The MIT Museum; p. 248 Peter S. Stevens, Patterns in Nature, Little, Brown, and Company, 1974, fig. 152, p. 183; p. 249 Dr. A.V. Grimstone; p. 250 top: Bruce Dale, © National Geographic Society; p. 250 bottom: Edward Weston; p. 251 Harold E. Edgerton, MIT; p. 252 top: B.J. Hammond; p. 252 bottom left: C.H. Waddington, "The Modular Principle and Biological Form," in Gyorgy Kepes, Module, Proportion, Symmetry, Rhythm, George Braziller, Inc., 1966, p. 22, fig. 2; p. 253 E.J. Bedford; p. 254 Mount Wilson and Palomar Observatories, © Carnegie Institution of Washington; p. 255 top: James E. Gelson; p. 255 bottom: © Loren McIntyre; p. 256 I.W. Bailey; p. 257 Jean Hanson and H.E. Huxley; p. 258 top: E.W. Muller; p. 258 bottom: W. Roggenkamp; p. 259 top: F.N.M. Brown; p. 259 bottom left: Tet Borsig; p. 259 bottom right: Tet Borsig; p. 260 Theodor Schwenk; p. 261 Cyril Stanley Smith, "Structure, Substructure, Superstructure," in Gyorgy Kepes, Structure in Art in Science, George Braziller, Inc., 1965, fig. 7, p. 33; p. 262 top left: Cyril Stanley Smith, "Structure, Substructure, Superstructure," in Gyorgy Kepes, Structure in Art in Science, George Braziller, Inc., 1965, fig. 6, p. 32; p. 262 top right: F.T. Lewis; p. 262 bottom: Peter S. Stevens, Patterns in Nature, Little, Brown, and Company, 1974, p. 177, fig. 146; p. 263 Peter S. Stevens, Patterns in Nature, Little, Brown, and Company, 1974, p. 141, fig. 1158; p. 264 Tet Borsig; p. 265 top: © The Harold E. Edgerton 1992 Trust, courtesy Palm Press, Inc.; p. 265 bottom: Gyorgy Kepes, The New Landscape, Paul Theobald and Co., 1956, fig. 190, p. 174; p. 266 Eastman Kodak Company; p. 267 Carl Struwe; p. 268 Dr. L. Wegmann; p. 269 © Charlie Orr/The Nature Conservancy; p. 270 Dr. R. Schenk; p. 271 top: H.J. Williams; p. 271 bottom: Peter S. Stevens, Patterns in Nature, Little, Brown, and Company, 1974, p. 221, fig. 182; p. 272 Nigel Calder, The Key to the Universe, Penguin Books, 1978, p. 121; p. 273 H.P. Roth; p. 274 W. Furneaux, British Butterflies and Moths, Longmans, Green & Co., 1932, plate V, fig. 1; p. 275 Peter S. Stevens, Patterns in Nature, Little, Brown, and Company, 1974, p. 82, fig. 54; p. 276 Thomas Hornbein; p. 277 top: Edward Weston; p. 278 Cyril Stanley Smith, "Structure, Substructure, Superstructure," in Gyorgy Kepes, Structure in Art in Science, George Braziller, Inc., 1965, fig. 2, p. 30; p. 279 top: D'Arcy Wentworth Thompson, On Growth and Form, Vol. II, Cambridge University Press, 1959, fig. 208, p. 538; p. 279 bottom: Theodore Andrea Cook, Spirals in Nature and Art, E.P. Dutton & Company, 1903, fig. 37; p. 280 top: D'Arcy Wentworth Thompson, On Growth and Form, Vol. II, Cambridge University Press, 1959, fig. 554, p. 1092; p. 280 bottom: Hans Christian von Baeyer, Taming the Atom, Random House, 1992, fig. 14; p. 281 © Ken Heyman; p. 282 Eastman Kodak Company; p. 283 Barry C. Bishop, National Geographic Image Collection; p. 284 U.S. Navy; p. 285 Dmitri Kessel, Time/Life, © Time, Inc.; p. 286 Georg Gerster, Photo Researchers; p. 287 top: Tet Borsig; p. 287 bottom: Evelyn Hofer; p. 288 H.J. Williams; p. 289 © 1990, Amon Carter Museum, Fort Worth, Texas, Bequest of Eliot Porter; p. 291 Loren McIntyre, National Geographic

Chapter 7

p. 300 Colin Thubron, Jerusalem, Time-Life Books, 1976, p. 123; p. 301 Rijksmuseum; p. 303 bottom left: Kari Haavisto; p. 303 bottom right: Christie's International Magazine, September-October 1988, p. 47; p. 304 top: Mountain Travel, Sobek: 1993 Adventure Annual by the Adventure Company, p. 12; p. 304 bottom: Kari Haavisto; p. 307 top left: © The Henry Moore Foundation; p. 307 bottom: Marguerite Duthuit-Matiase and Claude Duthuit, Henri Matisse, Vol. II, Claude Duthuit, Paris, Cat. #464, plate 70; p. 310 © Ken Heyman; p. 311 © William Garnett

Chapter 8

p. 322 top: Walker Evans; p. 322 bottom: Theo Crosby; p. 323 left: Gonul Oney, Turk Cini Sanati: Turkish Tile Art, Yapi ve Kredi Bankasi'nin bir Kultur Hizmetidir, 1976, p. 116; p. 323 right: Kakiemon Kiln; p. 324 left: Lefevre & Partners, London, Catalog of 71 Rare and Oriental Carpets and Textiles, Friday, February 3, 1978, #13; p. 324 right: Lefevre & Partners, London, Catalog of 71 Rare and Oriental Carpets and Textiles, Friday, February 3, 1978, #14; p. 325 Eric Arthur and Dudley Witney: The Barn: A Vonishing Landmark in North America, M.F. Feheley Arts Company Limited, 1972, p. 110, fig. a; p. 326 Arthur Upham Pope, A Survey of Persian Art, Vol. VII, Soroush Press, plate 200; p. 327 F.W. Funke; p. 328 top: Hirmer Fotoarchiv, Munich; p. 328 bottom: Magnus Bartlett; p. 329 top: D.A. Harissiadis; p. 329 bottom: Chicago Historical Society; p. 330 top left: Robert Grant; p. 330 top right: The Mies van der Rohe Archives, The Museum of Modern Art, New York; p. 330 center left: Leonardo Benevolo, History of Modern Architecture, Vol. II, MIT Press, 1971, p. 453, fig. 510; p. 330 center right: Boesiger/Girsberges, Le Corbusier 1910-60, George Wittenborn, Ind., 1960, p. 53; p. 330 bottom left: Aris Konstantinidis; p. 331 top left: George Knight; p. 331 center left: Paul Warchol; p. 331 center right: Michael Graves; p. 331 bottom right: Lucien Herve; p. 332 top left: Courtesy the Frank Lloyd Wright Foundation; p. 332 top right: Ezra Stoller, © ESTO; p. 332 bottom left: T. and R.

Annan; p. 332 bottom right: Martin Charles; p. 333 top left: G.C. Mars, Brickwork in Italy, American Face Brick Association, 1925, p. 119, plate 124; p. 333 bottom left: Aris Konstantinidis; p. 333 center right: Leonardo Benevolo, History of Modern Architecture, Vol. II, MIT Press, 1971, p. 799, fig. 981; p. 333 bottom right: Dimitris and Suzana Antonakakis, Lyttos Hotel, Wien, March-April 1988, p. 9; p. 338 top: Alex Starkey; p. 338 bottom: Barry Shapiro; p. 339 top: Hans Jurgen Hansen, Architecture in Wood, The Viking Press, Inc., 1971, p. 85, fig. a; p. 339 bottom: Foto Marburg; p. 340 top: © Eames Office; p. 341 Gonul Oney, Turk Cini Sanati: Turkish Tile Art, Yapi ve Kredi Bankasi'nin bir Kultur Hizmetidir, 1976, p. 34; p. 341 bottom: Chic Harris; p. 345 top: The Metropolitan Museum of Art, Rogers Fund, 1958, © 1999, MMA; p. 345 bottom: Yanni Petsopoulos, Tulips, Arabesques and Turbans: Desorative Arts from the Ottoman Empire, Abbeville Press, Inc., 1982, p. 72, plate 54; p. 346 top: Ulrich Schurmann, Caucasian Rugs, Klinkhardt and Biermann, Braunschweig, p. 73, plate 9; p. 346 bottom: Kurt Erdmann, The History of Early Turkish Carpet, Oguz Press, 1977, color plate III; p. 347 top: © The Metropolitan Museum of Art, photograph by Seth Joel; p. 347 bottom: © The Metropolitan Museum of Art, photograph by Seth Joel; p. 348 top: Art Resource; p. 348 bottom: Art Resource

Chapter 9

p. 358 V & A Picture Library, Photo Peter MacKinven

Chapter 10

pp. 384 to 392: Courtesy the Estate of Andre Kertesz; p. 410 Country Life Picture Library.

Although every effort has been made to trace and contact copyright holders before publication, this has not been possible in a few cases. If notified, we will be pleased to rectify any errors or omissions at the earliest opportunity.

THE FOUR BOOKS OF THE NATURE OF ORDER

BOOK ONE: THE PHENOMENON OF LIFE

BOOK TWO: THE PROCESS OF CREATING LIFE

BOOK THREE:A VISION OF A LIVING WORLD

BOOK FOUR: THE LUMINOUS GROUND